Collatz Problemi, diğer adıyla 3n+1 Problemi, matematikçileri onlarca yıldır meşgul eden çözülmesi zor bir muammadır. Dikkat edin. Bu problem sizi cezbedebilir.
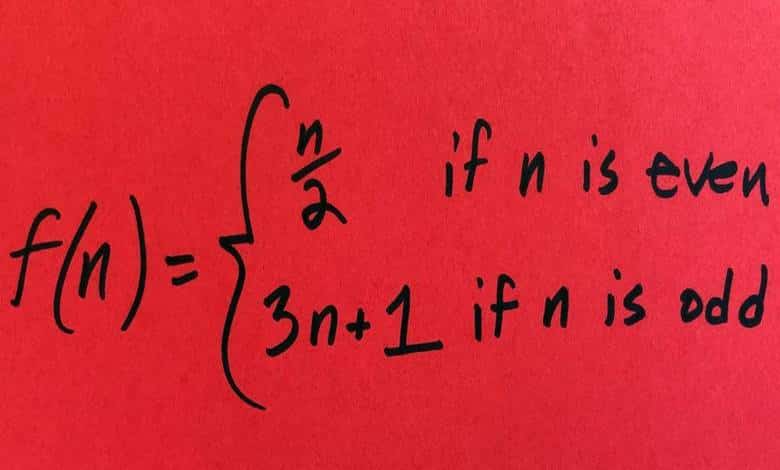
İlk bakışta bu problem saçma derecede basit görünecektir. Yine de uzmanlar onlarca yıldır boşuna çözüm arıyor. Matematikçi Jeffrey Lagarias’ın aktardığına göre, sayı teorisyeni Shizuo Kakutani bir zamanlar şöyle demiş: Soğuk Savaş döneminde “Yale Üniversitesi’nde yaklaşık bir ay boyunca herkes bu problem üzerinde çalıştı ama bir sonuca ulaşamadı. Benzer bir durum Chicago Üniversitesi’nde de yaşandı. Hatta bu problemin ABD’deki matematiksel araştırmaları yavaşlatmak için bir komplo olduğu yönünde espriler yapıldı.”
Kakutani’nin bahsettiği bu baş belası bulmaca, Collatz sanısı. Görünüşte basit olan bu problem, insanları kolayca içine çekip kaybettiriyor. Bu yüzden deneyimli hocalar, hevesli öğrencilerini bu tuzağa düşmemeleri için sıkça uyarıyor. Gerçek araştırmalarından sapmalarını istemiyorlar.
Collatz Problemi Nedir?
Sadece bir sayı seçin, herhangi bir sayı: Eğer çiftse, ikiye bölün; tekse, üçle çarpıp bir ekleyin. Ortaya çıkan yeni sayıyla aynı işlemi tekrar edin. Sonra tekrar. Tekse 3x + 1, çiftse x / 2. Bu işlemleri tekrar tekrar yapın. Collatz sanısına göre, hangi doğal sayıdan başlarsanız başlayın, sonunda mutlaka 1’e ulaşırsınız.

Mesela 10’u alın: 10 çift bir sayı, bu yüzden ikiye bölüyoruz, 5 oluyor. 5 tek olduğu için üçle çarpıp bir ekliyoruz, 16 ediyor. 16 çift, ikiye bölüyoruz: 8. Tekrar ikiye bölüyoruz: 4. Sonra 2, sonra 1. 1 tek sayı olduğu için üçle çarpıp bir ekliyoruz: 4. Ve artık döngüyü biliyoruz: 4 → 2 → 1 → 4… Sonsuza kadar bu şekilde gidiyor.
11’i deneyin: Tek sayı, üçle çarpıp bir ekliyoruz, 34. Çift, ikiye bölüyoruz, 17. Tek, üçle çarpıp bir ekliyoruz, 52. Çift, ikiye böl: 26. Yine ikiye böl: 13. Üçle çarp, bir ekle: 40. İkiye böl: 20, sonra 10, sonra 5. Üçle çarp bir ekle: 16. İkiye böl: 8, sonra 4, sonra 2, sonra 1. Ve yine döngüye girdik.
Elbette, 1’e ulaştıktan sonra işlemi sürdürmeye devam edebilirsiniz: 1’den 4, ardından 2 ve tekrar 1 gelir. Bu işlem döngüye girer ve sonsuza dek aynı şekilde devam eder. Bu yüzden, 1 sayısı bu sürecin doğal sonu olarak kabul edilir.
Collatz Problemi Aslında Bir Çok Farklı İsimde Karşımıza Çıkar
Collatz sanısı’nın kökeni belirsizdir; bu nedenle bu hipotez farklı adlarla anılır. Uzmanlar buna Syracuse problemi, Ulam problemi, 3n + 1 sanısı, Hasse algoritması ya da Kakutani problemi der.
Alman matematikçi Lothar Collatz, matematik eğitimi sırasında yinelemeli fonksiyonlara ilgi duymaya başladı ve bu alanda çalışmalar yaptı. 1930’lu yılların başında bu konuda bazı makaleler yayımladı, ancak bugün adıyla anılan bu problemin açık hesaplama kuralı bu makalelerde yer almıyordu. 1950’li ve 1960’lı yıllarda, özellikle Helmut Hasse ve Shizuo Kakutani gibi matematikçilerin bu problemi farklı üniversitelere — örneğin Syracuse Üniversitesi’ne — yaymasıyla Collatz sanısı ün kazandı.
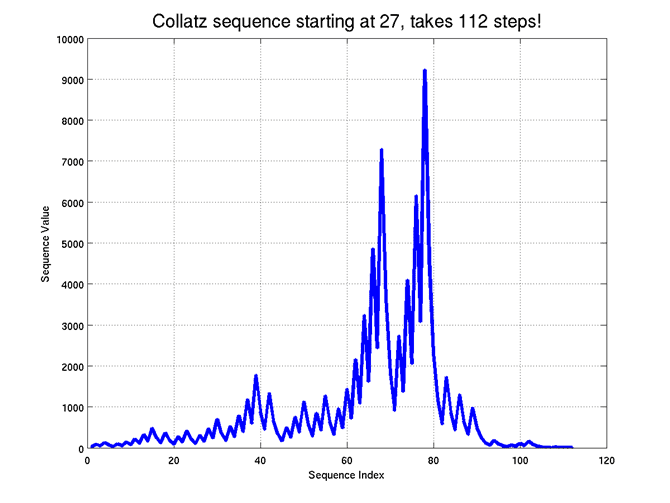
Bu basit görünen önerme matematikçileri büyüledi. Onlarca yıldır uzmanlar, Collatz işleminin belirli bir sayıya uygulandığında, yeterince tekrar edildiğinde mutlaka 1 sonucuna ulaştığını ispatlamaya çalışıyor. Bu ısrarın tek sebebi problemin sadeliği değil.
Collatz sanısı, matematiğin başka önemli sorularıyla da bağlantılı. Örneğin bu tür yinelemeli fonksiyonlar, gezegenlerin yörüngelerini tanımlayan modeller gibi dinamik sistemlerde karşımıza çıkar. Ayrıca bu sanı, asal sayıların dağılımını inceleyen sayı kuramının en eski problemlerinden biri olan Riemann sanısıyla da ilişkilidir.
Collatz Problemini Çözmek Mümkün mü?
Araştırmacılar 2019 ve 2020 yıllarında yürütülen ortak bir bilgisayar bilimi projesiyle Collatz sanısını 2⁶⁸’in altındaki tüm sayılar için test etti. Bu yaklaşık 3 x 10²⁰ farklı başlangıç değeri anlamına geliyor. Bu sayıların tamamı, Collatz sanısını sağlıyor.
Yani işlem tekrarlandığında hepsi sonunda 1’e ulaşıyor. Ancak bu, evrende başka bir yerde sanıya uymayan bir sayı olmadığını kanıtlamıyor. Öyle bir başlangıç değeri olabilir ki, Collatz işlemi tekrarlandıkça sayı sürekli büyür ve sonunda sonsuza ulaşır. Yine de istatistiksel olarak bu senaryo pek olası görünmüyor.
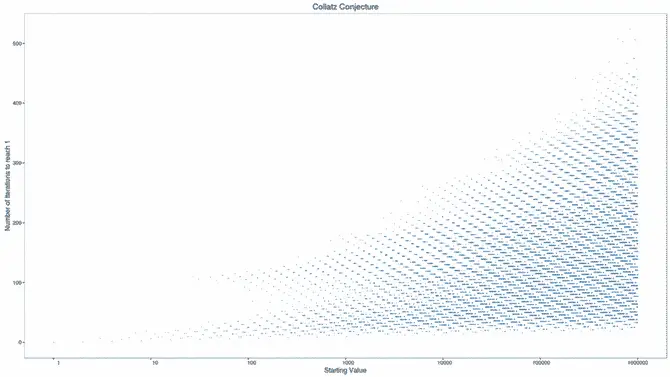
Ancak tüm bu istatistiksel değerlendirmelere rağmen, hala “4 → 2 → 1” dışında bir döngüye giren bir başlangıç değeri olması mümkündür. Böyle bir döngü, daha fazla sayıyı içeriyor da olabilir ve bu durumda işlem hiçbir zaman 1’e ulaşmaz. İşte bu olasılık, sanının ispatlanmamış kalmasının temel nedenlerinden biridir.
Kurala uymayan döngüler, Collatz sanısında negatif tam sayılara da izin verilirse ortaya çıkar. Bu durumda işlem yalnızca –2 → –1 → –2 → … gibi basit bir döngüde değil, aynı zamanda –5 → –14 → –7 → –20 → –10 → –5 → … ya da –17 → –50 → … → –17 → … gibi daha karmaşık döngülerde de sona erer. Ancak yalnızca doğal sayılarla (yani 1 ve üzeri pozitif tam sayılarla) sınırlandığımızda, bugüne kadar hiçbir uyumsuz döngü bulunamamıştır
Collatz Problemi Çözümsüz Olabilir mi?
Matematikçiler, Collatz sanısını kesin olarak kanıtlamak için onlarca yıldır uğraşıyor. Şimdiye kadarki en büyük ilerleme, 2019 yılında UCLA’den Fields Madalyası sahibi Terence Tao tarafından kaydedildi. Tao, doğal sayıların neredeyse tüm başlangıç değerlerinin eninde sonunda 1’e yakın bir değere ulaştığını ispatladı.
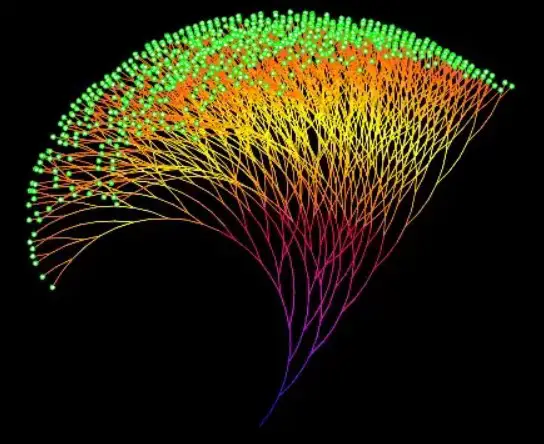
Ne yazık ki Tao’nun yöntemi istatistiksel dayanaklara dayandığı için tüm sayılar için genellenemiyor. Diğer tüm yöntemler de çıkmaza girmiş durumda. Bu da Collatz sanısının belki de yanlış olabileceği düşüncesini akla getiriyor.
Ünlü matematikçi Paul Erdős, Collatz Problemi için bir yorumunda, “Matematik henüz böyle problemlere hazır değil,” demiştir. Bu yorum, problemin ne kadar karmaşık ve derin bir matematiksel meydan okuma olduğunu özetliyor.
Belki de bu sanı gerçekten mevcut matematiksel araçlarla ispatlanamayacak türde bir problem. 1987’de matematikçi John Horton Conway, Collatz sanısının genelleştirilmiş bir versiyonunu inceledi ve bazı yinelemeli fonksiyonların doğası gereği ispatlanamaz özellikler taşıdığını gösterdi. Belki de Collatz sanısı da bu kapsama giriyor.
Sonucunda Collatz problemi hala çözümsüz. Ancak yine de şu anda bir yerlerde yüzlerce kişi bu probleme kafa yormaya devam ediyor. Esasen matematiğin güzelliği de zaten budur. Yine de hatırlatalım. 268‘den küçük her sayı için bu problem doğrulanmıştır.
Dolayısıyla, bir karşı örnek arıyorsanız, yaklaşık 300 kentilyondan başlamalısınız. Bu nedenle denemek isteyenlere şimdiden sabırlar diliyoruz. Yazının devamında göz atmanızı öneririz: Bugüne Kadar Çözülmüş En Zor 9 Matematik Problemi
Kaynaklar ve ileri okumalar:
- The Simple Math Problem We Still Can’t Solve. Yayınlanma tarihi: 23 Eylül 2020; Bağlantı: The Simple Math Problem We Still Can’t Solve/
- Mathematician Proves Huge Result on ‘Dangerous’ Problem; yayınlanma tarihi: 11 Aralık 2019; Bağlantı: Mathematician Proves Huge Result on ‘Dangerous’ Problem/
Matematiksel





