“Hareket yasaları ve ondan türetilenler veya başka şekilde gözlenenler esasında doğanın aynı esaslarına dayanır. Hayvanların hareketlerini, bitkilerin büyümelerini gözlemlediğimizde hepsi en az eylem ihtiyacının bir sonucudur.” – Pierre Louis Maupertuis.

Varyasyon hesabı, bir sistemin hangi koşullarda en iyi ya da en kötü sonucu verdiğini inceleyen matematik dalıdır. Bir başka ifadeyle, belirli bir niceliği en büyük ya da en küçük yapan şekli, yolu ya da fonksiyonu bulmayı amaçlar. Bugün fizik, mühendislik ve matematiğin birçok alanı bu yöntem üzerine kuruludur.
Bu fikirler yeni değildir. 1700 yıl önce İskenderiyeli Pappus, bal peteklerinin neden altıgen olduğunu açıklarken aynı mantığı sezmişti. Özellikle Pierre Louis Maupertuis, en az eylem ilkesini açıkça formüle eden ilk kişilerden biri oldu.
Leonhard Euler, 1744 yılında yayımladığı eserle bu dağınık fikirleri tek bir yöntem altında topladı ve varyasyon hesabının temellerini attı. Varyasyon hesabının çıkış noktası, fizikçilerin daha sonra en az eylem ilkesi adını vereceği prensipti.
En Az Eylem İlkesi Nedir?
Bu ilkeye göre doğadaki sistemler —gezegenlerin yörüngeleri, bir taşın düşüşü, ışığın yayılması— bir anlamda “en az çaba” gerektiren yolu izler. Buradaki “çaba”, fizikte eylem adı verilen matematiksel bir niceliktir. Eylem doğru biçimde tanımlandığında, doğanın nasıl hareket ettiğini belirlemek mümkün olur.
Euler, dirençsiz hareket eden bir cisim için eylemi kesin biçimde tanımladı. Bir cismin nerede ve ne zaman başladığını, nerede ve ne zaman bittiğini biliyorsak, varyasyon hesabı başlangıç ve bitişi birleştiren ve eylemi en aza indiren yolu belirler. İlkenin söylediğine göre cisim tam da bu yolu izler. Hesaplamalar yapılınca Newton’un hareket yasalarının bu yöntemden kendiliğinden çıktığı görülür.
Euler’in ardından Joseph-Louis Lagrange bu yöntemi soyutlayarak geliştirdi. Bugün varyasyon hesabının kalbinde yer alan denklem onların adını taşır: Euler-Lagrange denklemi. William Rowan Hamilton ise 19. yüzyılda bu yaklaşımı modern hâline getirdi ve en az eylem ilkesini çağdaş fiziğin merkezine yerleştirdi.
En Az Eylem İlkesi Nasıl Açıklanır?
Tek değişkenli basit bir fonksiyonu düşünelim: f(x). Türev df/dx, bu fonksiyonun her noktadaki eğimini verir. Grafiğe baktığınızda şunu hemen fark edersiniz: Fonksiyon bir tepenin zirvesinde ya da bir vadinin tabanında olduğunda, yani yerel maksimum ya da yerel minimum yaptığında türev tam olarak sıfırdır. Çünkü bu noktalarda fonksiyon ne yukarı ne aşağı gider.
Bu fikir, en kısa eğriyi bulmanın matematiksel temelini oluşturur. Tüm olası eğriler kümesini düşünelim. Her eğri için bir sayı belirleyen bir fonksiyon tanımlarız; bu sayı eğrinin uzunluğudur.
Şimdi bu eğriyi hayalimizde çok küçük miktarlarda değiştirelim. Biraz yukarı bükebiliriz, biraz aşağı çekebiliriz, biraz sola kaydırabiliriz. Yani eğriyi sonsuz küçük şekillerde bozabileceğimiz sınırsız sayıda yön vardır.
Eğer elimizdeki eğri gerçekten en kısa yolsa, yaptığımız hiçbir küçük değişiklik onu daha da kısaltamaz. Bu yüzden uzunlukta oluşacak değişimin türevi her yönde sıfır çıkar. Böylece “en kısa yol” fikri, “eğri uzayında uzunluk fonksiyonunun türevi her yönde sıfırdır” şeklinde kesin bir matematiksel koşula dönüşür.
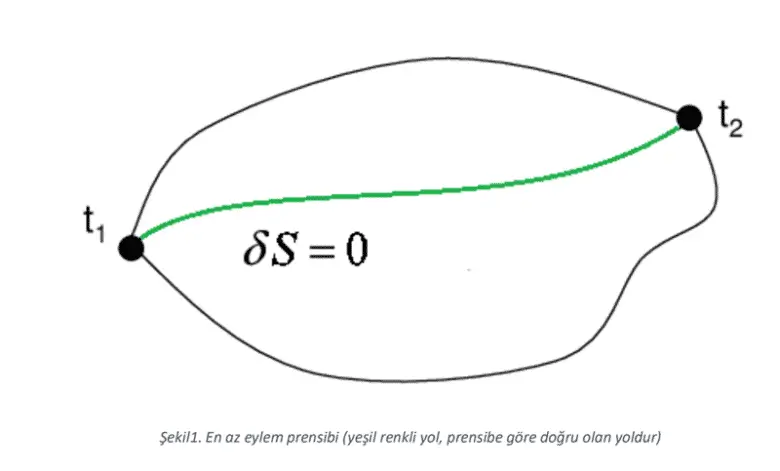
Anacak amacımız bir eğrinin uzunluğunu değil, doğanın gerçekten neyi “azalttığını” anlamak. Bunun için, havaya bir taş attığınızı düşünün. Bu taş yere düşene kadar kıvrımlı bir yol izler. Ancak bu yol düz değildir, yani en kısa yol değildir.
Öyleyse doğa burada uzunluğu değil, başka bir niceliği en aza indirir. Bu niceliğe eylem denir. Bir parçacık hareket ederken her anda bir konumu x ve bir hızı v vardır. Bu iki bilgi bize o anda, ne kadar kinetik enerjiye sahip olduğunu ve konumundan dolayı ne kadar potansiyel enerji taşıdığını söyler.
Lagrange fonksiyonu (veya kısaca Lagrangian), bu iki enerjinin farkıdır. Yani: L = kinetik enerji – potansiyel enerji. Bu L fonksiyonu, parçacığın yolunun her noktasında bir değer alır. Bir yolun toplam eylemi, L’nin zaman boyunca toplanmasıdır. Doğanın seçtiği gerçek yol, işte bu toplam eylemi en az yapan yoldur. Eylemi s olarak düşünürseniz de aşağıdaki formül karşımıza çıkar.
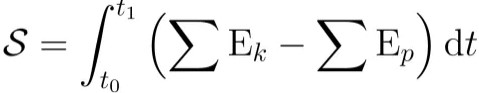
Lagrange fonksiyonu yolun her noktasında —yani her anda— belirli bir sayısal değer alır. Buna karşılık eylem, yolun tek tek noktalarına değil, bütün yolun tamamına bağlıdır. Bir parçacığın başlangıç ve bitiş konumları ile zamanları verildiğinde, parçacığın gerçekten izleyeceği yol, bu iki nokta arasında hayal edebileceğimiz tüm olası yollar içinde eylemi en küçük olan yoldur.
Sonuç olarak
Klasik mekaniği bu şekilde ifade etme biçimine Lagrange mekaniği denir; çünkü burada temel büyüklük Lagrange fonksiyonudur. Eylem, Lagrange fonksiyonunun zaman boyunca toplanmasıyla elde edilir ve doğada gerçekleşen gerçek hareketler, bu toplamı en aza indiren hareketlerdir.
Kaynaklar ve ileri okumalar
- Michopoulos, Dimosthenis. (2024). The Principle of Least Action as the Fundamental Physical Law. 10.13140/RG.2.2.34316.94088.
- Wen, Yong-Li & Wang, Yunfei & Tian, Li-Man & Zhang, Shanchao & Li, Jianfeng & Du. Jing-Song & Yan, Hui & Zhu, Shi-Liang. (2023). Demonstration of the quantum principle of least action with single photons. Nature Photonics. 17. 1-6. 10.1038/s41566-023-01212-1.
- Explaining the Principle of Least Action: Physics Mini Lesson; Bağlantı: https://www.youtube.com/
Matematiksel