1978 yılında Fransa’nın Marsilya kentinde düzenlenen bir matematik konferansında, organizatörler programa son dakika bir ekleme yapılacağını duyurdu. Matematikçi Roger Apéry, matematik dünyasının en ünlü sayılarından birinin — Apéry sabiti olarak da bilinen ζ(3)’ün — iki tam sayının oranı şeklinde yazılamayacağını kanıtlayacaktı. Apéry’nin bu kanıtı, matematik camiasında büyük bir heyecan ve şaşkınlık yarattı.

Konferans katılımcıları şüpheliydi. Matematikçiler yüzyıllardır ζ(3)’ün irrasyonelliğini kanıtlamaya çalışmış, hatta dönemin en parlak isimlerinden biri olan İsviçreli matematikçi Leonhard Euler bile bu problemi çözmekte başarısız olmuştu. Şimdi ise, 60’lı yaşlarında, çok da tanınmayan bir Fransız matematikçi olan Roger Apéry, bu yüzyıllık bilmecenin çözümünü bulduğunu iddia ediyordu.
Sunum kısa sürede bir kaosa dönüştü. Apéry, neredeyse hiç açıklama yapmadan denklem üzerine denklem sıraladı. Konuşmasını Fransızca yapıyor, arada şakalarla konuyu yumuşatıyor, ancak ispatın temel noktalarına dair kritik açıklamaları atlıyordu

Örneğin, konuşmasının başında tahtaya, daha önce kimsenin görmediği ancak ispatının temelini oluşturan bir denklem yazdı. Salondakiler bu denklemin nereden geldiğini sorduğunda, Apéry yalnızca “Bahçemde yetişiyorlar” şeklinde cevap verdi. Bu yanıtsızlık ve alaycı üslup, birçok matematikçinin yerinden kalkıp salonu terk etmesine neden oldu.
Ancak en az bir kişi, konuşmadan Apéry’nin haklı olduğuna ikna olmuş şekilde ayrıldı. Henri Cohen, sunumda verilen argümanın temel fikrini kavradı ve hemen çalışmaya koyuldu. Birkaç ay içinde, bir grup matematikçiyle birlikte ispatın eksik kısımlarını tamamladı.
Apery Sabiti Nedir?
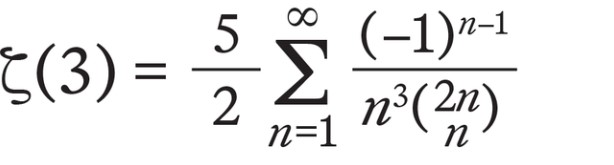
Yaklaşık iki ay sonra, Apéry’nin gerçekten de Euler’in 200 yıl önce başaramadığı şeyi başardığı anlaşıldı: ζ(3)’ün irrasyonel bir sayı olduğu kesin biçimde kanıtlanmıştı. Matematikçiler Apéry’nin ispatını kabul ettikten sonra, peş peşe gelecek yeni sonuçları sabırsızlıkla beklemeye başladı.
Ancak durum çok da beklendiği gibi olmadı. Matematikçiler, Apéry’nin yönteminin yeni ilerlemelerin yolunu açabileceğini umuyordu. Herkes, tüm zeta fonksiyonu değerlerinin irrasyonel olduğunu kanıtlamanın sadece bir-iki yıl meselesi olduğunu düşünüyordu.
Bugün hâlâ Apery Sabitinin tam olarak hangi matematiksel yapıyla bağlantılı olduğunu anlamaya çalışıyoruz ve bu sorunun cevabına ulaşmaktan oldukça uzağız.
Euler’in Kaçırdığı Bir İspat
Matematiksel keşfin en eski dönemlerinden beri insanlar, hangi sayıların rasyonel olduğunu sorgulamıştır. İki buçuk bin yıl önce Pisagorcular, her sayının iki tam sayının oranı olduğuna inanıyordu. Ancak bir okul üyesi, √2’nin böyle bir oranla ifade edilemeyeceğini kanıtlayınca büyük bir şok yaşadılar.
√2 yalnızca bir başlangıçtı. Matematiğin farklı alanlarından sayısız özel sayı ortaya çıkmaya başladı. Bazıları, π gibi, alan ve hacim hesaplarında karşımıza çıkar. Diğerleri ise belirli fonksiyonlarla bağlantılıdır — örneğin e, doğal logaritmanın tabanıdır.
Yine de yüzyıllar boyunca, belirli sayıların irrasyonelliğine dair kanıtlar oldukça seyrek olmuştur. 1700’lerde, büyük matematikçi Leonhard Euler e sayısının irrasyonelliğini kanıtladı; Johann Lambert ise aynı sonucu π için gösterdi. Euler ayrıca tüm çift zeta değerlerinin π’nin bir kuvvetiyle çarpılmış rasyonel sayılara eşit olduğunu gösterdi. Bu ispat, nihayet 1800’lerin sonlarında tamamlandı.
Matematikçilerin hâlâ bu kadar temel bir sayı sorusuyla uğraşıyor olması şaşırtıcı gelecektir. Ancak bir sayının irrasyonel olduğunu kanıtlamak için araştırmacıların elinde çok az araç vardır. Üstelik bu araçlar çoğu zaman yetersiz kalır.
Yöntemlerden biri tüm paydaları kademeli olarak eleyen sonsuz bir kesir dizisini incelemektir. Ancak bu da kolay değildir. Bazen doğru dizi şans eseri karşınıza çıkar. Örneğin, yaklaşık 2.71828 olan e sayısı, aşağıdaki sonsuz toplamla ifade edilmektedir.
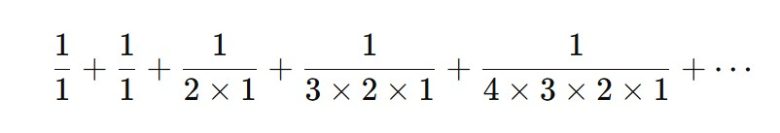
Bu toplamı herhangi bir noktada durdurup o ana kadar olan terimleri toplarsanız, bir kesir elde edersiniz. Ve yalnızca lise düzeyindeki matematikle, bu kesir dizisinin e’ye yeterince hızlı yaklaştığını ve bu sayede tüm olası paydaları saf dışı bırakabildiğini göstermek mümkündür. Apéry’nin irrasyonel sayısı olan ζ(3), şu şekilde tanımlanan bir sonsuz toplamdır.
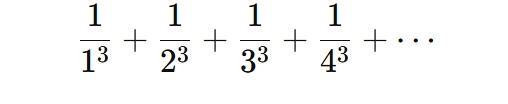
Bu toplamı herhangi bir adımda durdurup o noktaya kadar olan terimleri toplarsanız, bir kesir elde edersiniz. Fakat bu kesirler, ζ(3)‘e yeterince hızlı yaklaşmaz.
Apéry’nin dahiyane çözümü, ζ(3)’e çok daha hızlı yaklaşan farklı bir kesir dizisi oluşturmaktı. Bu diziyi oluştururken, yüzyıllar öncesine dayanan matematiksel araçları kullandı. Hatta bir makalede bu ispat, “Euler’in gözden kaçırdığı ispat” olarak tanımlanmıştı.
Zeta Fonksiyonu Nedir ve Neden Önemlidir?
Apéry’nin ispatı son derece akıllıca düşünülmüştü. Ancak matematikçileri asıl heyecanlandıran ispatın kendisi değildi. Onların asıl istediği, önemli sayıların irrasyonelliğini kanıtlamaktı. Önemli sayı deyince de akla ilk gelen Riemann zeta fonksiyonu ve onunla ilişkili olan L-fonksiyonlarının değerleridir.
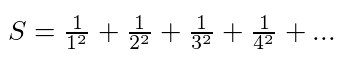
1644’te İtalyan matematikçi Pietro Mengoli, kare sayıların terslerinin toplamını merak etti ancak sonucu bulamadı. Dönemin pek çok matematikçisi soruyu çözemedi.
Bu problemin çözümü 90 yıl sonra, yine Basel’de doğan 27 yaşındaki Leonhard Euler’den geldi. Euler, bu sorunun çözümünü vererek sonsuz toplamın sonucunu gösterdi. Euler, bu problemi çözmek için bugün ζ(s) olarak bilinen zeta fonksiyonunu tanımladı. Basel problemi, bu fonksiyonun özel bir durumu olan ζ(2) değerine karşılık geliyordu.
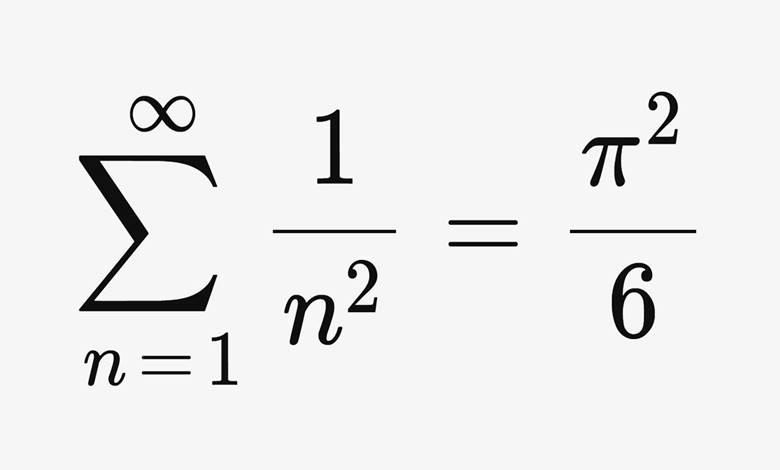
Euler, zeta fonksiyonunun tüm çift tam sayı değerleri için (s = 2k) kesin sonuçlar elde etti; ζ(2), ζ(4), ζ(6) gibi değerleri π’nin kuvvetleriyle ifade etmeyi başardı.
Ancak s tek sayı olduğunda, Euler sonucun ne olacağını belirleyemedi. Özellikle ζ(3), ζ(5), ζ(7) gibi değerlerin irrasyonel olup olmadığını açıklığa kavuşturamadı. Bu sorular, 20. yüzyılda Roger Apéry’nin çığır açan ispatına kadar yanıtsız kaldı.
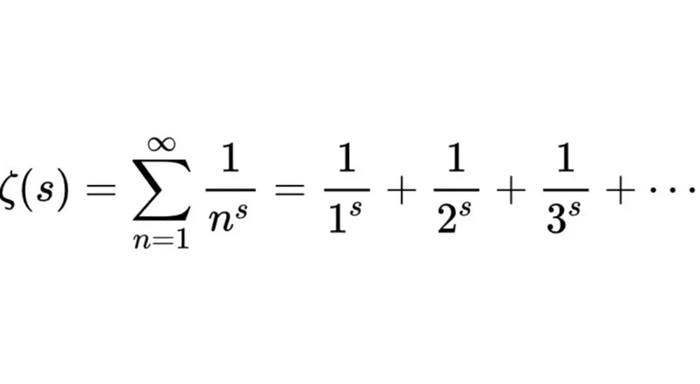
Zeta fonksiyonu, zamanla matematiğin en büyük gizemlerinden biriyle ilişkilendirildi. Bu ilginin kaynağı, 19. yüzyılda Bernhard Riemann’ın fonksiyonu karmaşık sayılar için de tanımlamasıydı. 1859’da Riemann, bu fonksiyonu kullanarak daha sonra “Riemann Hipotezi” olarak bilinecek iddiasını ortaya attı.
Zeta fonksiyonu, uzun zamandır asal sayıların dağılımıyla yakından ilişkili bir yapı olarak bilinmektedir.. Benzer şekilde, L-fonksiyonları da zeta fonksiyonuna benzer, ancak payları farklıdır. Bu fonksiyonlar, daha karmaşık sayı sistemlerinde asal sayıların nasıl dağıldığını anlamamıza yardımcı olur.
Apery Sabiti Sadece Gizemli Bir Sabit Değildir
20. yüzyılda bu sayı fiziğe de sıçradı: Kuantum mekaniği ve elektrodinamik gibi alanlarda beklenmedik biçimde ortaya çıkmaya başladı. Böylece ζ(3), sadece sayı teorisinde değil, modern fiziğin temelinde de önemli bir yere sahip oldu.
1940’larda, araştırmacılar elektromanyetizmanın kuantum teorisini geliştirdi. Bu teoriye göre vakum tamamen boş değil; kısa ömürlü parçacık-karşıt parçacık çiftleriyle doludur. Bu çiftler yoktan var olur ve hemen yok olarak bir tür kuantum parıltısı oluşturur.
Örneğin, iki elektronun saçılmasını hesaplarken bu geçici parçacıkları da dikkate almak gerekir çünkü elektronların hareketini etkilerler. İşte bu kuantum etkisini açıklamak için ζ(3) değeri kullanılır.
Fiziksel hesaplamalar için, ζ(3) değerinin birkaç ondalık basamağını bilmek yeterlidir. Ancak matematikçiler, için bu asla yeterli olmayacaktır.
Kaynaklar ve İleri Okumalar:
- Mysterious Constant that Makes Mathematicians Despair. Yayınlanma tarihi: 19 Aralık 2024. Kaynak site: Scientific American. Bağlantı: Mysterious Constant that Makes Mathematicians Despair
- Rational or Not? This Basic Math Question Took Decades to Answer.. Yayınlanma tarihi: 5 Ocak 2025. Kaynak site: Quanta Magazine. Bağlantı: Rational or Not? This Basic Math Question Took Decades to Answer.
Matematiksel





