Altın oran, yüzyıllardır sanat ve bilimle ilgilenen birçok kişiyi etkileyen bir matematiksel kavramdır. Ancak bu ilgi, zaman zaman yanlış yorumlar ve abartılı iddialarla gölgelenir.

Popüler kültürde sıkça karşımıza çıkan bu oran, Da Vinci Şifresi gibi eserlerde anılır. Matematiğin gerçek hayattaki rolünü göstermek amacıyla kitaplarda, makalelerde ve okul projelerinde sıkça kullanılır.
Bazıları doğadaki estetik desenlerin temelinde altın oranın bulunduğunu savunur; bu nedenle ona zaman zaman “ilahi oran” da denir. Sanat ve mimarlıkta da birçok eserin bu oranla ilişkili olduğu ileri sürülür.

Matematikle ilgilenmeyenler bile Mısır piramitlerinin, Yunan tapınaklarının, Mona Lisa’nın ya da insan vücudunun altın orana göre şekillendiği görüşünü duymuştur. Oysa bu oranın bazı önemi olsa da, ona atfedilen gizemlerin çoğu bilimsel dayanaktan yoksundur.
Altın Oran Nedir?
İki nicelikten büyük olanı a, küçük olanı b olsun. Eğer bu iki nicelik, yani a/b oranı, toplamlarının büyük olana oranına — yani (a + b)/a — eşitse, bu oran altın orandır. Yunan alfabesindeki phi (φ) harfiyle gösterilen altın oranın değeri (1 + √5)/2 olup, yaklaşık olarak 1,6180339887… şeklinde sürer.
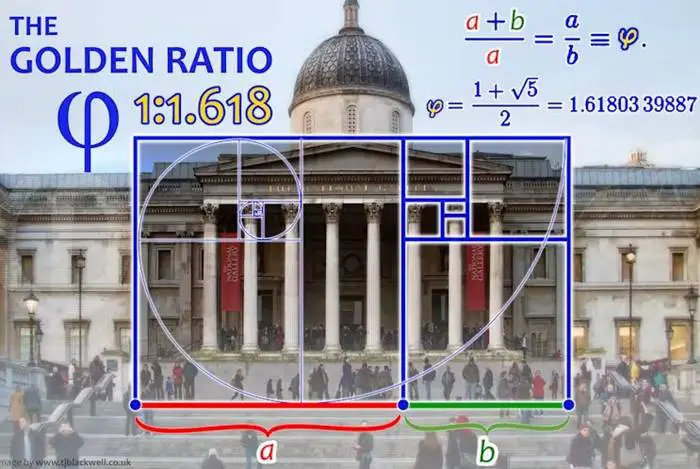
Altın oran, tıpkı pi gibi irrasyoneldir; yani iki tam sayının oranı olarak yazılamaz ve ondalık açılımı sonsuzdur, tekrar etmez. Ancak pi’den farklı olarak, tam sayı katsayılı bir cebirsel denklemin kökü olarak ifade edilebilir. Bu yüzden transandantal değildir.
“φ” sembolü, oranı kompozisyonlarında kullandığı düşünülen ünlü Yunan heykeltıraş Phidias’a (MÖ 490–430) bir gönderme olarak seçilmiştir. Phidias’ın ismi Yunanca’da φ harfiyle başladığı için bu sembolle
Sanat Ve Mimaride Altın Oran Miti Nedir?
Bir dikdörtgenin kenarları altın oranı sağlıyorsa, bu biçime altın dikdörtgen denir. Bazı sanatçılar, kompozisyonlarını bilinçli olarak bu oranı taşıyan tuvaller üzerine inşa etmiştir. Salvador Dalí’nin The Sacrament of the Last Supper adlı yapıtı buna iyi bir örnektir. Tablo 166,7 × 267 cm ölçülerindedir ve bu oran altın dikdörtgene karşılık gelir.

Dalí, altın oranı yalnızca tuvalin boyutlarında kullanmakla kalmaz; sahneyi de bu orana göre düzenler. Masanın üst kenarını, resmin yüksekliği boyunca altın oran noktasına yerleştirir. İsa’nın sağında ve solunda duran iki havariyi ise yatayda aynı oransal konumlara oturtur. Tüm sahne, on iki yüzlü bir geometrik cisim olan büyük bir dodekahedronun içine yerleştirilmiştir. Beşgen pencerelerden, Dalí’nin doğduğu Katalonya manzarası görünür.
Düzenli bir dodekahedronun her beşgen yüzünün merkezinde, üç altın dikdörtgenin kesişimi yer alır. Ayrıca (φ + 1):1 ve φ:1 oranına sahip dikdörtgenler de bu katı cisim içinde tam olarak yer bulur. Dalí, resimdeki geometrik düzeni bu matematiksel yapıyla açıkça ilişkilendirir.
Dalí’nin bu İncil sahnesinde altın oranı kullanma fikrini, büyük ihtimalle Leonardo da Vinci’den esinle gelişmişti. Leonardo’nun Son Akşam Yemeği tablosunda mekânın, masanın ve bazı ögelerin altın oranla örtüştüğü sıkça dile getirilir. Ancak bunun bilinçli bir tercih mi yoksa rastlantı mı olduğu kesin değildir.
Benzer iddialar Mona Lisa için de vardır. Yüz çevresine bir altın dikdörtgen çizilebildiği söylenir. Fakat bunun kasıtlı olup olmadığı tartışmalıdır; ayrıca bu çerçevenin tam olarak nereden geçirilmesi gerektiği konusunda da fikir birliği yoktur.

Buna karşılık kesin olan bir nokta vardır. Leonardo, matematikçi ve Fransisken rahip Luca Pacioli’nin yakın dostuydu. Pacioli, 1509’da altın oran üzerine De Divina Proportione adlı üç ciltlik bir eser yayımladı. Bu kitabın çizimlerini Leonardo yaptı.
Altın Oran İle Fibonacci Sayıları Neden İlişkilidir?
Phi, matematikte pi kadar dikkat çekici bir sayıdır ve beklenmedik birçok yerde karşımıza çıkar. En güçlü ilişkilerinden biri, yaklaşık 1200 yılında Leonardo Fibonacci’nin tanımladığı Fibonacci dizisidir. Bu dizi 0 ve 1 ile başlar; her yeni terim, kendisinden önce gelen iki terimin toplamıdır.
Ardışık Fibonacci sayılarının oranı, sayı büyüdükçe phi değerine yaklaşır. Bu yakınlık yalnızca sayısal bir özellik değildir. Fibonacci ölçülerine sahip bitişik dikdörtgenler içine çizilen eğri, spiral bir şekil oluşturur. Bu spiral; deniz kabuklarında, dalgalarda, ayçiçeği tohumlarında ve gül yapraklarının dizilişinde sıkça karşımıza çıkar.

Phi’nin matematikteki yaygınlığı ve doğada beklenmedik biçimde ortaya çıkması, Rönesans düşünürlerinin ona “ilahi” bir statü vermesinin de nedenidir.
On dördüncü ile on yedinci yüzyıllar arasında, düşünürler hızla genişleyen bilgi evrenini kapsayıcı bir felsefe içinde birleştirmeye çalışıyordu. Bu çerçeve hem yeryüzünü hem gökyüzünü kapsıyor ve doğaüstü öğelere de yer veriyordu.
Bu arayışın merkezindeki önemli isimlerden biri, Alman astronom ve matematikçi Johannes Kepler’di. Kepler, evrenin uyum, denge ve matematiksel simetriye dayalı katı yasalarla düzenlendiğine inanıyordu.
Kepler, De nive sexangula adlı denemesinde altın oranı ve Fibonacci dizisini; düzgün çokgenler, kar taneleri ve çiçek yapraklarının yapısal düzeniyle birlikte ele aldı. Ona göre geometri, insanlık tarihindeki en değerli iki matematiksel keşfi içeriyordu: Biri Pisagor teoremi, diğeri ise bir doğru parçasının altın orana bölünmesiydi. Kepler, bu iki kuramı doğanın simetrisi ve evrensel düzeniyle doğrudan ilişkilendiriyordu.
Altın Oran Ve Güzellik İlişkisi
Daha yakın dönemde bazı araştırmacılar, altın oranın insan zihni için özel bir estetik çekiciliğe sahip olduğunu öne sürmüştür. Bu yaklaşımın erken örneklerinden biri, Alman fizikçi ve psikolog Gustav Fechner’in 1860’larda yaptığı deneylerdir.
Fechner, katılımcılara farklı en-boy oranlarına sahip dikdörtgenler göstererek en hoş bulduklarını seçmelerini istemiştir. Tercihler, oranları 1,50, 1,62 ve 1,75 olan üç dikdörtgende yoğunlaşmış; en çok beğenilen ise 1,62 oranına sahip, yani altın orana yakın olan dikdörtgen olmuştur.

Fechner bu çalışmayla yetinmemiş; pencere çerçeveleri, müze tabloları ve kitap sayfalarının oranlarını da ölçerek incelemiştir. Vorschule der Aesthetik adlı eserinde, bu ölçümlerin ortalamasının altın orana oldukça yakın olduğunu ileri sürmüştür. Ancak bu sonuçların ne ölçüde seçici örnekleme ve yorum etkisi taşıdığı, günümüzde hâlâ tartışma konusudur.
Tartışmayı araştırmacılar insan yüzü algısına taşıdı. Bazı araştırmacılar, yüzün belirli oranları altın orana yaklaştıkça daha çekici algılandığını iddia etti. Ortodontist Mark Lowey, 1994’te yayımladığı çalışmada manken yüzlerinin bu eğilimi gösterdiğini öne sürdü.
Ancak araştırmacılar bu iddiayı kısa sürede geçersiz kıldı. Aynı hastanenin çene cerrahisi biriminde Alfred Linney ve ekibi, lazerle manken yüzlerini son derece hassas biçimde ölçtü. Elde ettikleri veriler nettir. Manken yüzlerinin oranları, genel nüfusa kıyasla ne daha düzenlidir ne de daha “altın oranlıdır.”
Sonuç Olarak
Bir sonraki proje konunuz “Altın Oran Nedir, Doğada Nerede Görülür?” olacaksa, konuyu mutlaka bilimsel gerçeklerle popüler mitleri ayırarak ele alın. Ancak bu ayrımı yaparak matematiğin hem gücünü hem de sınırlarını doğru biçimde gösterebilirsiniz.
Kaynak ve ileri okumalar:
- Naini, F.B. The golden ratio—dispelling the myth. Maxillofac Plast Reconstr Surg 46, 2 (2024). https://doi.org/10.1186/s40902-024-00411-2
- Mark Chu-Carroll; A Geek’s Guide to the Beauty of Numbers. Logic, and Computation; 2013 The Pragmatic Programmers, LLC.
- Myths of maths: The golden ratio; yayınlanma tarihi: 23 Şubat 2020; Bağlantı: https://plus.maths.org/
- Martines, G. The Relationship Between Architecture and Mathematics in the. Pantheon. Nexus Netw J 2, 57–62 (2000). https://doi.org/10.1007/s00004-999-0008-6
- The Golden Mean: a great discovery or natural phenomenon? Yayınlanma tarihi: 3 Kasım 2013. Kaynak site: Conversation. Bağlantı: he Golden Mean: a great discovery or natural phenomenon?
Matematiksel





