Sayı teorisinin en dikkat çekici varsayımlarından biri olan ABC varsayımı, son derece basit görünen bir denklemle başlar: a + b = c.
2012 yılı, sayı teorisyenleri için adeta bir dönüm noktasıydı. Japonya’daki Kyoto Üniversitesi’nden ünlü matematikçi Shinichi Mochizuki, alanın en önemli çözülmemiş problemlerinden biri olan abc varsayımı için bir ispat yayımladı.
Ancak bu heyecan kısa sürede yerini hayal kırıklığına bıraktı. Mochizuki, 20 yıl boyunca tamamen kendi geliştirdiği, son derece özgün bir matematiksel sistem kurmuştu. Bu sistem, diğer uzmanlar tarafından anlaşılması son derece güç bir yapıdaydı.
Geçen on yıl boyunca birçok matematikçi bu ispat üzerinde çalıştı. Ancak düzenlenen pek çok konferansa rağmen abc varsayımının durumu netlik kazanmadı. Bu belirsizliği ortadan kaldırmak amacıyla, Japon medya ve telekomünikasyon şirketi DWANGO’nun kurucusu Nobuo Kawakami, Mochizuki’nin ispatında temel bir hata ortaya koyan bir makale yazan kişiye 1 milyon dolara kadar ödül vaat etti.

ABC Varsayımı Nedir?
İlk bakışta, abc varsayımı oldukça zararsız gibi görünecektir. Bu hipotez, iki doğal sayı olan a ve b’nin toplamının c’ye eşit olduğu a + b = c ilişkisine dayanır. Sayı teorisinde sıkça karşılaşılan durumlarda olduğu gibi, burada da asal çarpanlar—yani sayıları bölen asal sayılar—ön plandadır.
Her doğal sayı, asal çarpanlarının çarpımı şeklinde, örneğin, 15 sayısı 3 × 5 olarak, 324 sayısı ise 2² × 3⁴ biçiminde yazılır. Özellikle 324 gibi bazı asal çarpanları birden fazla kez içeren sayılar “zengin” olarak adlandırılır.
Bu tür zengin sayılar nadiren görülürken, iki zengin sayının toplamının yine zengin bir sayı olması çok daha istisnai bir durumdur. 1985 yılında Joseph Oesterlé ve David Masser tarafından ortaya atılan abc varsayımı, tam olarak bu alışılmadık durumu inceler.
Bu varsayım, iki sayının toplamının ne kadar “zengin” olabileceğine dair bir üst sınır koyar. Ancak onu bu kadar önemli kılan ise, doğal sayıların toplama ve çarpma özelliklerini aynı denklemde birleştirmesidir.
ABC Varsayımı Neden Önemlidir?

Basit görünümlü a + b = c denklemi pek çok matematiksel problemle yakından ilişkilidir. Bunun en bilinen örneklerinden biri, aⁿ + bⁿ = cⁿ biçimindeki denklemleri ele alan Fermat’nın Son Teoremi’dir. Bu teorem, 350 yılı aşkın bir süre boyunca matematikçilerin çözmekte zorlandığı bir bilmece olmuştur.
Nihayetinde, 1990’ların ortalarında Andrew Wiles, n > 2 olduğunda bu denklemin a, b, c için hiçbir tam sayı çözümü bulunmadığını kanıtlamayı başarmıştır.
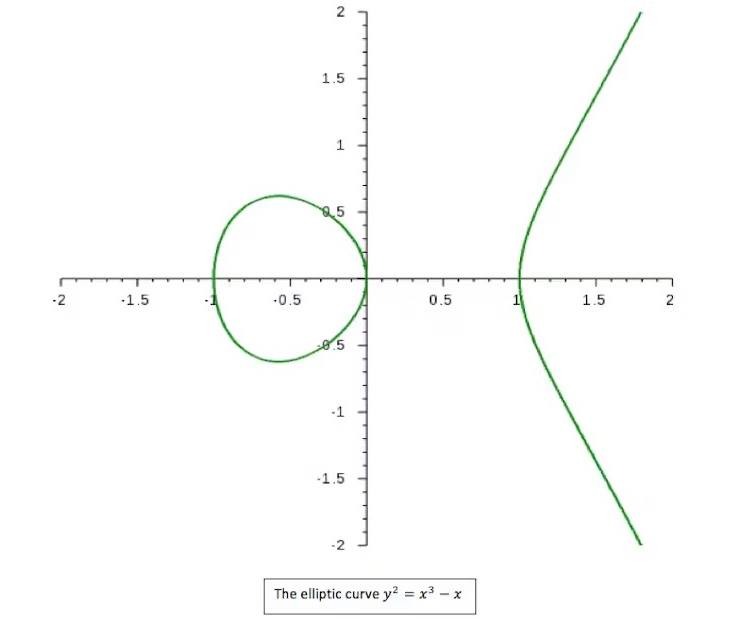
Bu varsayım doğru kabul edilirse, Fermat’nın teoremi çok daha basit bir şekilde açıklanacaktır. Özellikle eliptik eğrilerle bir arada değerlendirildiğinde ise, matematik alanında son derece güçlü bir araç haline gelme potansiyeline sahiptir.
ABC Varsayımı İçin Milyon Dolarlık Motivasyon
Bu nedenle, Shinichi Mochizuki’nin çalışmasının yayımlanması, sayı teorisiyle ilgilenen birçok araştırmacının ilgisini üzerine topladı. Zaten önemli başarılarla tanınan Japon matematikçi, abc varsayımını kanıtlamayı hedefleyen “Evrensel-ötesi Teichmüller Kuramı”nı (IUT) geliştirmişti.
Ancak bu teori, yüzlerce sayfa boyunca süren karmaşık tanımlar ve teoremlerden oluşuyordu. Dahası, bazı ispatlarda yalnızca “İspat tanımdan çıkmaktadır” ifadesi yer alıyordu.

2018’de Peter Scholze ve Jakob Stix, “Why ABC Is Still a Conjecture” başlıklı makalelerinde Mochizuki’nin ispatında ciddi bir sorun bulduklarını öne sürdü. İkili, konuyu tartışmak için Japonya’ya gitse de ortak bir sonuca varılamadı.
2021’de Mochizuki’nin ispatı, gözden geçirilmiş bir biçimde, başeditörü olduğu Publications of the Research Institute for Mathematical Sciences dergisinde yayımlandı.
Ancak Mochizuki’nin son yayınına rağmen çoğu sayı kuramcısı ispatı takip edemiyor. Üstelik alandaki genel kanı, argümanlarının abc varsayımını kanıtlamadığı yönünde. Yani a + b = c bilmecesi hâlâ çözülmüş değil.

Bu alandaki belirsizliği gidermek amacıyla DWANGO’nun kurucusu Nobuo Kawakami dikkat çekici bir adım attı. Önümüzdeki on yıl boyunca her yıl 20.000 ila 100.000 dolar arasında değişen bir ödül verileceğini belirtti. Bu ödül, IUT kuramında anlamlı bir ilerleme sunan çalışmalara, uzmanlardan oluşan bir kurulun değerlendirmesiyle takdim edilecek
Bunun yanı sıra, kuramda ciddi bir hata tespit eden kişiye 1 milyon dolar ödül verilecek. Bu ikinci ödülün hangi hakemli çalışmaya verileceğine ise doğrudan Kawakami karar verecek. Amacının, bu alanda daha fazla bilimsel araştırmayı teşvik etmek olduğunu bir basın toplantısında dile getirdi.
Sonuç Olarak
Matematikçi Fumiharu Kato bir demeçte, dünyada IUT kuramını anlayan kişi sayısının ondan az olduğunu ifade etmişti. Bu nedenle, Kawakami’nin girişiminin somut sonuçlar doğurup doğurmayacağı ve abc varsayımının açıklığa kavuşup kavuşmayacağı henüz netlik kazanmış değil.
Mochizuki, blog yazısında şu ifadeye yer verdi. “Çalışmamı anlamak için öncelikle yıllardır benimsediğiniz ve zihinlerinize yerleşmiş şablonları kırmanız şart.” Belki de onun çalışmalarının hâlâ tam olarak anlaşılamamış olmasının nedeni budur.
Kaynaklar ve ileri okumalar
- Castelvecchi D. Mathematical proof that rocked number theory will be published. Nature. 2020 Apr;580(7802):177. doi: 10.1038/d41586-020-00998-2. PMID: 32246118.
- Decade-long struggle over maths proof could be decided by $1m prize. Yayınlanma tarihi: 11 Temmuz 2023. Kaynak site: New Scientist. Bağlantı: Decade-long struggle over maths proof could be decided by $1m prize
- $1 Million Will Go to the Mathematician Who Busts the ‘ABC Conjecture’ Theory. Yayınlanma tarihi: 28 Temmuz 2023. Kaynak site: Scientificamerican. Bağlantı: $1 Million Will Go to the Mathematician Who Busts the ‘ABC Conjecture’ Theory
- Mochizuki, Shinichi. (2021). Inter-universal Teichmüller Theory IV: Log-Volume Computations and Set-Theoretic Foundations. Publications of the Research Institute for Mathematical Sciences. 57. 627-723. 10.4171/PRIMS/57-1-4.
- Joshi, Kirti. (2025). Final Report on the Mochizuki-Scholze-Stix Controversy. 10.48550/arXiv.2505.10568.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





