Matematikte zaman zaman beklenmedik durumlarla karşılaşırız. Bunlardan biri, 1951 yılında Alfred Moessner tarafından keşfedildi. Aynı yıl, bu keşfin geçerliliği Oskar Perron tarafından matematiksel olarak kanıtlandı. Bugün bu sonuç “Moessner Teoremi” olarak bilinse de, çoğu kişi tarafından “Moessner Mucizesi” adıyla anılır.

Birçok kişi, ardışık pozitif tek sayıların toplamıyla ilgili şu formüle aşinadır: 1 + 3 + 5 + … + (2n – 1) = n². Bu toplamı geometrik olarak da göstermek mümkündür. Böylece herhangi bir ispat yapmadan, sadece şekle bakarak formülün neden doğru olduğunu fark edebilirsiniz.
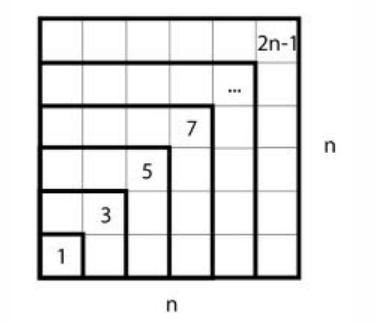
Yukarıda gördüğünüz ispat, aslında Pisagor’a aittir. Bu ispat o kadar beğenilmiştir ki, uzun süre boyunca kimse yeni bir yöntem arayışına girmemiştir. Ancak yaklaşık yetmiş yıl önce Alfred Moessner konuya farklı bir bakış açısıyla yaklaşınca durum değişti. Moessner, bulgularını 1951 yılında yayımladı. Fakat çalışmanın Almanca olarak yayımlanması nedeniyle, başlangıçta fazla dikkat çekmedi.

Alfred Moessner Tam Olarak Ne Yapmıştı?
Alfred Moessner, bazı tanıdık sayı dizilerinin şaşırtıcı ve alışılmadık yöntemlerle elde edilebileceğini keşfetti. Şimdi onun bakış açısıyla düşünmeye çalışalım.

Önce sayma sayılarını yan yana yazın. Ardından her ikinci sayıyı daire içine alın. Daire içine alınmayan sayıların kümülatif toplamlarını bulun. Dikkat ederseniz, elde ettiğiniz sonuçlar tam kare sayılardır.
Bu sonuç, daha önce gördüğümüz formülle aynıdır. Bu size fazla şaşırtıcı gelmemiş olabilir. Ancak Moessner burada durmadı.
Sayma sayılarını yeniden yazın. Bu kez her üç sayıda bir sayı daire içine alınsın. Sonra da daire içine alınmayan sayıların, bulunduğu pozisyona kadar olan kümülatif toplamlarını bulun ve alt satıra yazın. İkinci satırda, aynı şekilde, her ikinci sayıyı daire içine alın. Kalan sayıların toplamlarını bir alt satıra yazın. Sonuçta bir şey fark ettiniz mi?
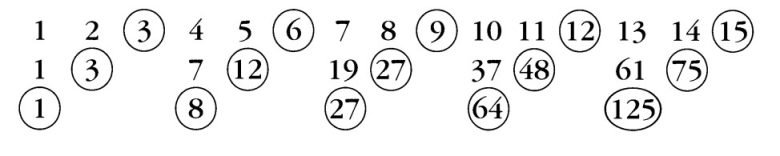
Evet, sizin de fark ettiğiniz gibi, elde ettiğimiz sayılar—yani 1, 8, 27, 64 ve 125—sırasıyla 1, 2, 3, 4 ve 5 sayılarının küpleridir. Muhtemelen bugüne kadar hiç kimse pozitif tam sayıların küplerini elde etmek için bu yöntemi düşünmemiştir.
Moessner Mucize Teoremi Ortaya Çıkıyor
Aslında bu noktada durmak zorunda değiliz. Aynı işlemi bu kez her dört sayıda bir sayıyı daire içine alarak uygulayalım. Ardından daire içine alınmayan sayıların kümülatif toplamlarını bulalım.
İlk satırda her dört sayıda bir, ikinci satırda her üç sayıda bir, üçüncü satırda ise her iki sayıda bir sayıyı daire içine aldık. Sonra, her seferinde daire içine alınmayan sayıların o noktaya kadar olan toplamlarını alt satıra yazdık. Elde ettiğimiz sayılar—1, 16, 81 ve 256—sırasıyla 1, 2, 3 ve 4 sayılarının dördüncü kuvvetleridir.
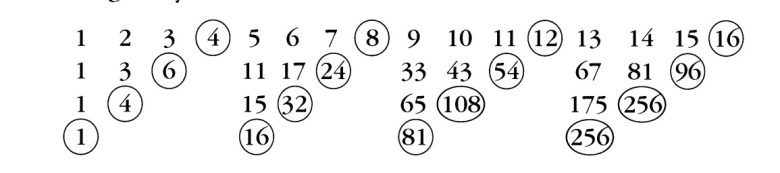
Bu noktada artık bir genelleme yapabiliriz. Ancak öncesinde son bir örnek daha inceleyelim. Bu kez 1 + 2 + 3 + … + n toplamını elde etmeye çalışalım.
Aşağıda göreceğiniz gibi, önce her 1 sayıda bir, sonra her 2 sayıda bir, ardından her 3 sayıda bir sayıyı daire içine alalım. Her satırda, daire içine alınmayan sayıların toplamını alt satıra yazalım. Peki bu sefer ne fark ettiniz? Evet: 2 = 2!, 6 = 3!, 24 = 4!, 120 = 5! Sonuçlarımız giderek daha ilginç bir hâl alıyor.
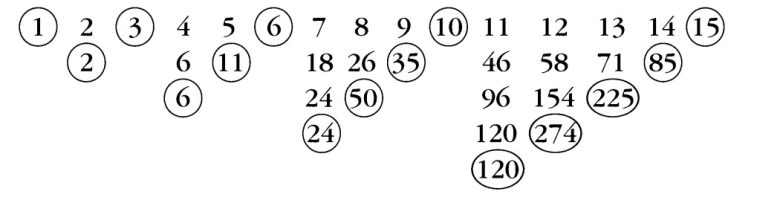
Bu Teoremin Bir İspatı Var mı?
Sonuç olarak Moessner Teoremi bize şunu söyler: Pozitif tam sayıları sırayla yazın. Ardından, her n. terimi diziden çıkarın (başka bir deyişle, daire içine alın) ve geriye kalan sayıların kısmi toplamlar dizisini oluşturun. Daha sonra, bu yeni dizideki her (n–1). terimi çıkarın ve yeniden kısmi toplamları hesaplayın. Bu işlemi aynı şekilde devam ettirdiğinizde, elde ettiğiniz son dizi, pozitif tam sayıların n. kuvvetlerini verir.
Eğer bu yazıyı buraya kadar okuduysanız, büyük olasılıkla bu işlemlerin nasıl işe yaradığını merak etmişsinizdir. Aslında, Moessner’in kendisinin bile bunu tam olarak anlayıp anlamadığını bilmiyoruz. Çünkü yalnızca bir sayfalık çalışmasında herhangi bir ispat yer almıyordu.
Yıllar içinde, matematikçiler bu sıra dışı teoremle ilgilenmeye başladı. Sonunda matematikçi Oskar Perron bir ispat geliştirmeyi başardı. Ancak bu ispat, bir web sayfasında açıkça aktarılabilecek kadar basit değildir. (Kaynaklar bölümünde erişebileceğiniz bir videoda bu teoremin görsel bir ispatı sunulmaktadır.)
Matematikçiler farklı ispatlar aramayı sürdürürken, siz de Moessner Mucizesi’ni kendiniz deneyebilirsiniz. Üstelik bu sayı dizisinin yalnızca kuvvetler veya faktöriyellerle sınırlı olmadığı, başka ilginç özellikler de barındırabileceği düşünülüyor. Denemenin hem öğretici hem de eğlenceli olacağını düşünüyoruz.
Yazıdan sonra okumaya devam etmek isterseniz: Hesap Makinesinden Hızlı Toplama Yaparak Arkadaşlarınızı Şaşırtın!
Kaynaklar ve ileri okumalar
- J. H. Conway and R. K. Guy, 1996: Moessner’s magic. In The Book of Numbers, pages 63–65. Springer-Verlag.
- Moessner’s Magical Method; yayınlanma tarihi: 14 Temmuz 2019; Bağlantı: https://thatsmaths.com/
- Moessner’s theorem; bağlantı: https://en.wikipedia.org/wiki/Moessner%27s_theorem
- The Moessner Miracle. Why wasn’t this discovered for over 2000 years?; Yayınlanma tarihi: 17 Temmuz 2021; Bağlantı: https://www.youtube.com
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





