Öklid, Zor Ölüm 3 ve Bir Bidon Problemi

Biraz eskilerde kalsa da, Zor Ölüm 3 filminden hatırlayacağınız bir matematik problemi vardır: “Elimde biri 3 litrelik, diğeri 5 litrelik iki bidon su var. Bunları kullanarak tam olarak 4 litreyi nasıl elde edebiliriz?” Filmde bomba uzmanları bombayı imha edebilmek için bu soruyu çözmek zorundadır. Neyse ki tam zamanında soru çözülür, bomba etkisiz hale getirilir ve film mutlu sona bağlanır.

Bu problem son derece basit gözükse de aslında aralarında asal sayıları bulmaya yarayan çok eski bir probleme dayanmaktadır. Öklid, Zor Ölüm bilmecesine benzer, aralarında asal sayı problemlerini çözmenin bir yolunu 2300 sene önce bulmuştu. Probleme geçmeden kısa bir iki bilgi verelim…

Aralarında asal sayılar nedir?

Aralarında asal sayılar 1 hariç ortak böleni olmayan tamsayılardır. İki sayının aralarında asal sayı olması için kendilerinin asal olması gerekmez. Örneğin 15 ve 16 sayıları asal olmamalarına rağmen ortak bölenleri olmadığı için aralarında asaldır.

Şimdi problemi aritmetiğe dökelim. Tek bir farkla elimizde bir de boş 3. bidonumuz olsun. Aşağıdaki eşitlikte göreceğiniz “p” birinci ölçümüz ve “q” ikinci ölçümüzü sembolize ediyor. Burada p<q ve p ile q sayıları aralarında asal olmalı. k<q şartını sağlayan k ise elde etmek istediğimiz sonuç. Bu durumda eşitlik mp+nq=k olur. Sayılar teorisine fazla girmeden biz bunun pratikte nasıl kullanılacağına değinelim.

m sayısı p’nin kaç defa doldurulacağını veya boşaltılacağını, n sayısı q’nin kaç defa doldurulacağını veya boşaltılacağını belirlesin. Denklemde m veya n yanında artı olursa anlamı doldurmak ve eksi olursa anlamını boşaltmak olarak düşünelim. Filmdeki sorumuzu bu denkleme uygularsak p=3, q=5 ve k=4 olur yani 3m+5k=4

Şimdi bu şartı sağlayan tamsayıları aramamız gerekiyor. Görebileceğiniz gibi m=3 ve q=-1 olduğunda bu şart sağlanır. (3×3)+ (-1×5)=4. Yani üç litrelik sürahiyi üç kez doldurup beş litrelik sürahiyi bir kez boşaltarak dört litre elde ederek bu bidon problemini çözebiliriz. Aynı biçimde m=-2 ve n=2 olduğunda da sağlanır. (-2×3)+(2×5)=4

Gördüğünüz gibi sayılar teorisi ile ilgili bir kavram rahatlıkla uygulamaya dökülebiliyor. Burada eğer p ve q sayıları aralarında asal olmazsa birbirlerinin katı olacakları yada ortak bölenleri olacağı için bir çözüm bulunması mümkün olmuyor. İşte size matematik ne işe yarar ki sorusunun cevabı…

Bidon Problemi Nasıl Çözülür?

Filmdeki sorunun çözümüne gelelim. Anlaşılmasını kolaylaştırmak adına 5 litrelik bidona A, 3 litrelik bidona B diyelim. Ayrıca elimizde sınırsız suyumuz var ve 3. bir bidonumuz da yok.

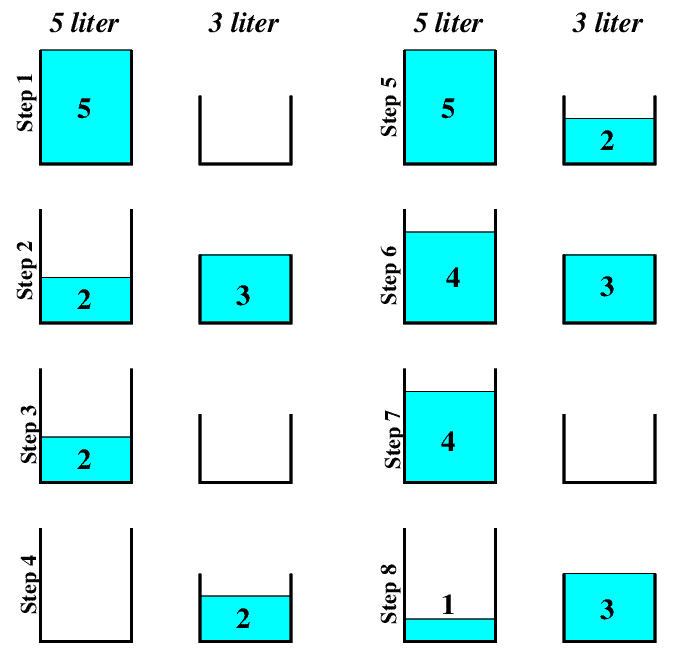
Önce A doldurulmalıdır. Ardından A’dan 3 litre B’ye aktarılır. Bu durumda A’da 2 litre suyumuz kaldı. Sonrasında B boşaltılır ve A’da kalan su ile tekrar doldurulur. Yani A’da su yokken B’de 2 litre su toplanmıştır. A bir kere daha ağzına kadar doldurulur ve B’yi tamamlar. Zaten B’nin 1 litreye ihtiyacı vardı. Bu durumda A’da 4 litre su kalır ve soru tamamlanır.

Bu arada bir dip not. Bu soru Oxford üniversitesi matematik bölümüne giriş mülakatlarında sorulan sorulardan bir tanesidir. Elbette amaçlanan adayın sadece problemi çözmesi değil, özgün düşünce biçiminin gözlemlenebilmesidir. Teorem hakkında daha detaylı bilgi için buraya göz atabilirsiniz.

Kaynaklar ve ileri okumalar:

• The Die Hard 3 Problem; http://www.math.tamu.edu
• John Fardon – Do You Think You Are Clever?
• Solve the famous water puzzle from Die Hard 3. Yayınlanma tarihi: 25 Mayıs 2020; Bağlantı: https://www.popsci.com/

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel