Sürekli Kesirler: Sayıları Göstermenin Farklı Bir Yolu

22/7, irrasyonel bir sayı olan π (pi)’ye öylesine yakın bir yaklaşık değer sunar ki, bu benzerlik her yıl 22 Temmuz’da “Pi Yaklaşım Günü” olarak kutlanır. Peki, bu kadar isabetli rasyonel tahminler nasıl elde ediliyor? Cevap, sayıların yapısına derinlemesine ulaşmamızı sağlayan sürekli kesirler yönteminde gizlidir.

Sayıları temsil etmenin pek çok yolu vardır: ondalık sistem, kesirli ifadeler, logaritmalar, üstel gösterimler… Her biri farklı matematiksel ihtiyaçlara çözüm sunar. Ancak, genellikle göz ardı edilen ve matematiksel anlatımlarda nadiren yer verilen bir yöntem daha vardır: sürekli kesirler. Bu yöntem sayesinde, irrasyonel sayılara en yakın rasyonel değerler de yüksek doğrulukla elde edilir. Bu özelliği de onu oldukça güçlü bir araç haline getirir.

Sürekli Kesirler Nedir?

Sürekli kesirleri, ilk kez 6. yüzyılda Aryabhata kullandı. Avrupa’da bu yöntem 15. ve 16. yüzyıllarda yeniden gündeme geldi. “Continued fraction” terimi 1653’te John Wallis’in Arithmetica Infinitorum adlı eserinde ortaya çıktı. 18. ve 19. yüzyıllarda Euler ve Gauss, bu yapının matematiksel temellerini ayrıntılı biçimde ortaya koydu.

Sürekli kesirler, aslında kesirlerin içinde yer alan başka kesirlerden oluşur. Her sayıyı—ister rasyonel ister irrasyonel olsun—bir sürekli kesir olarak ifade etmek olasıdır. Bu yapıları sistemli bir şekilde yazmak için, şimdilik yalnızca pay kısmı 1 olan ve paydalarında pozitif tam sayıların yer aldığı biçimlere odaklanacağız. Genel anlamda bir sürekli kesir aşağıdaki gibi ifade edilecektir.

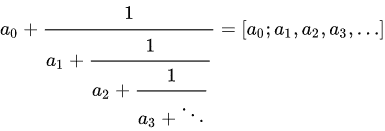
Diyelim ki 72 / 19 kesrinin sürekli kesir karşılığını bulmak istiyoruz. İlk adım, 72’nin içinde kaç tane 19 olduğunu ve geriye kalanı hesaplamak olacaktır. Basit bir bölmeyle 72’yi, 3 × 19 + 15 şeklinde yazabiliriz. Şimdi aynı işlemi 19 ve 15 için uyguluyoruz: 19 = 1 × 15 + 4. Devam ediyoruz, çünkü henüz kalanı sıfıra indiremedik. Bu durumda aşağıdaki adımları gerçekleştireceğiz.

• 15 = 3 × 4 + 3.
• 4 = 1 × 3 + 1.
• 3 = 3 × 1 + 0.

Yukarıdaki işlemlerde yer alan çarpanları sırasıyla yazdığınızda, aradığınız sürekli kesir ortaya çıkacaktır. Bu arada matematikle ilgilenen bir okur, aslında bu işlemlerin Öklid algoritmasının adımları olduğunu fark edecektir.

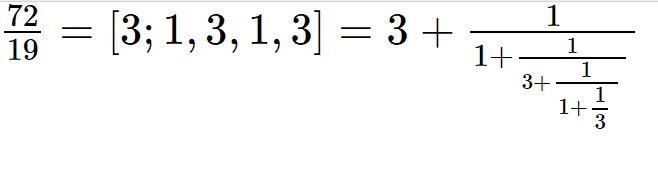
Sürekli kesirler, yukarıdaki örnekte olduğu gibi sonlu ya da sonsuz uzunlukta olur. Sonlu uzunlukta olan sürekli kesirler, en alttan başlayarak katman katman hesaplanır ve her zaman bir rasyonel sayı verir. Öte yandan, bazıları sonsuz uzunluktadır ve irrasyonel sayıların temsili için kullanılır. Bir örneğini aşağıda görebilirsiniz.

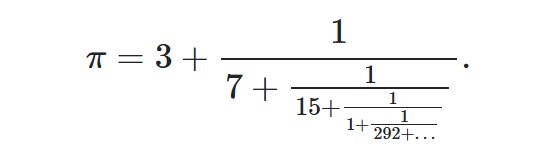
Sürekli Kesirler İle Nasıl İşlem Yapılır?

Bazı durumlarda, bu kesirlerle işlem yapmak şaşırtıcı derecede kolaydır. Örneğin, bir kesrin çarpmaya göre tersini almak istediğinizde yapmanız gereken tek şey, kesri ters çevirmektir. Eğer elimizde çok uzun bir sürekli kesir varsa, bununla ters alma işlemi yapılamayacağını düşünmek yanlıştır.

Mesela 2.3456 ondalık sayısı sürekli kesir biçiminde [2; 2, 3, 1, 3, 4, 5, 6, 4] şeklinde olur. Bu sayının çarpmaya göre tersini almak istiyorsanız, yapmanız gereken tek şey başına bir sıfır eklemektir. Yani ters çevrilmiş hali [0; 2, 2, 3, 1, 3, 4, 5, 6, 4] biçimindedir. Eğer başlangıçta zaten bir sıfır varsa, bu kez o sıfırı kaldırmanız yeterlidir.

Sürekli kesirlerin bir diğer avantajı da, irrasyonel sayılarla yapılan işlemlerde ortaya çıkar. Örneğin √2’nin ondalık yaklaşık değeri 1.4142135623730951’dir. Ancak bu sayı sürekli kesir olarak [1; 2, 2, 2, 2, 2,…] biçiminde yazılır ve bu düzen sonsuza kadar devam eder. Bu periyodik yapı, sayının irrasyonelliğini göstermekle kalmaz, aynı zamanda hesaplamalarda düzenli bir örüntü sunduğu için pratik bir avantaj sağlar.

Bir sürekli kesiri belli bir noktadan sonra keserseniz, ortaya çıkan ifade “yakınsak” olarak adlandırılır. Bu yakınsaklar, ilgili sayıya ait en iyi rasyonel yaklaşık değerleri verir. Tabii burada “en iyi” ifadesi mutlak bir yakınlığı değil, bir dengeyi temsil eder. Çünkü irrasyonel bir sayıya ne kadar yaklaşmak isterseniz, her zaman daha hassas bir kesir bulabilirsiniz.

.Yakınlık tek başına yeterli değildir; paydanın büyüklüğü de önemlidir. Yaklaşım ne kadar isabetli olursa olsun, devasa bir payda bu değeri pratik olmaktan çıkarabilir. Sürekli kesirlerin avantajı tam da burada ortaya çıkar: Sayıya olabildiğince yaklaşırken, bunu mümkün olan en küçük paydalarla yaparlar. Bu nedenle, bulabileceğiniz en verimli yaklaşık değerler genellikle sürekli kesirlerden gelir.

Peki Bu Ne İşe Yarar?

İlginç matematiksel özelliklerinin ötesinde, bu kesirlerin gerçekten işe yarar bir yönü var mı? Özellikle bilgisayarlar açısından bu sorunun cevabı kesinlikle evet. Bu durumu 1972 yılında Bill Gosper ortaya koydu.

Gosper, sürekli kesirleri kullanarak bugün “lazy evaluation” olarak bilinen programlama yaklaşımının temelini attı. Bu çalışmayla birlikte, sürekli kesirler bilgisayar programlarında doğrudan kullanılabilecek bir yapıya kavuştu.

---

Kaynaklar ve ileri okumalar:

• Mark C. Chu-Carroll; A Geek’s Guide to the Beauty of Numbers, Logic, and Computation; 2013 The Pragmatic Programmers
• Different ways of looking at numbers; Yayınlanma tarihi: 6 Ocak 2000; Bağlantı: https://plus.maths.org/
• What’s So Great about Continued Fractions? Yayınlanma tarihi: 17 Mart 2015; Bağlantı: https://blogs.scientificamerican.com/

---

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel