Sicherman zarları, yüzlerinde standart zarlar gibi 1’den 6’ya kadar sayılar bulunmayan, buna rağmen iki zar birlikte atıldığında ortaya çıkan toplamların olasılık dağılımını sıradan zarlarla birebir koruyan özel bir zar çiftidir. Dışarıdan bakıldığında alışılmadık görünen bu zarlar, olasılık açısından tamamen adil bir oyun sunar.

Tavla oynayan pek çok kişinin bildiği gibi, iki zar atıldığında toplamın yedi gelme olasılığı diğer tüm toplamların olasılıklarından daha yüksektir. Yediden daha küçük ve daha büyük toplamların olasılıkları ise, aşağıda görüldüğü gibi, simetrik biçimde azalır.
- 2 = 1+1
- 3 = 1+2, 2+1
- 4 = 1+3, 2+2, 3+1
- 5 = 1+4, 2+3, 3+2, 4+1
- 6 = 1+5, 2+4, 3+3, 4+2, 5+1
- 7 = 1+6, 2+5, 3+4, 4+3, 5+2, 6+1
- 8 = 2+6, 3+5, 4+4, 5+3, 6+2
- 9 = 3+6, 4+5, 5+4, 6+3
- 10 = 4+6, 5+5, 6+4
- 11 = 5+6, 6+5
- 12 = 6+6
Peki zarların yüzlerini farklı sayılarla etiketlesek, yine de atıldıklarında aynı toplam olasılıklarını elde edebilir miyiz? Bu soruyu 1970’lerde matematikçi George Sicherman ele aldı. Verdiği yanıt şaşırtıcıydı: Evet, bu mümkündür.
Gerçekten de böyle bir zar çifti vardır. Birinci zarın yüzleri 1, 2, 2, 3, 3 ve 4’tür. İkinci zarın yüzlerinde ise 1, 3, 4, 5, 6 ve 8 sayıları yer alır. Yüzleri standart zarlar gibi görünmese de, bu iki zar birlikte atıldığında elde edilen toplamların olasılık dağılımı sıradan zarlarla birebir aynıdır. Günümüzde bu özel zar çiftine Sicherman zarları adı verilir.
Sicherman zarları nedir?
Yanıt, bir zarı bir polinom olarak ifade etmekte yatar. Polinomdaki her terimde, x’in üssü yüz değerini, katsayı ise o değere sahip yüzlerin sayısını temsil eder. Bu durumda sıradan bir altı yüzlü zar şu polinomla gösterilir: x + x² + x³ + x⁴ + x⁵ + x⁶
İki zarı birlikte düşündüğümüzde, bu polinomları çarparız. Bir zar xᵃ, diğeri xᵇ getirirse, toplam a + b olur ve bu da xᵃ⁺ᵇ terimine karşılık gelir. Dolayısıyla iki standart zarın toplamlarını veren ifade şudur:
(x + x² + x³ + x⁴ + x⁵ + x⁶)²= x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹²
Bu ifade, iki zar atıldığında ortaya çıkan olasılık dağılımını bire bir temsil eder. Polinomda xᶜ teriminin katsayısı, toplamı c olan kaç farklı atış kombinasyonu bulunduğunu gösterir. Örneğin x⁷’nin katsayısı 6’dır; çünkü iki zarla 7 elde etmenin altı farklı yolu vardır.
Sicherman zarları problemi tam olarak burada ortaya çıkar. Amaç, bu aynı polinomu, yani aynı olasılık dağılımını, farklı iki polinomun çarpımı olarak yazmaktır. Bu da standart olmayan yüzlere sahip, ama yine de tamamen adil olan bir zar çiftinin var olabileceğini gösterir.
Bunu yaparken bazı zorunlu koşulları göz önünde tutarız. Öncelikle zarların üzerinde boş yüz olamaz. Bu nedenle polinomlarda terimi yer alamaz. Ayrıca her zar altı yüzlüdür; yani her bir polinomdaki katsayıların toplamı 6 olmalıdır.
Son olarak, elde ettiğimiz yeni çarpanlar, orijinal polinomun tüm çarpanlarını içermek zorundadır. Aksi hâlde olasılık dağılımı değişir ve zarlar “adil” olmaktan çıkar. Bu yüzden işe tek zarın polinomunu çarpanlarına ayırarak başlarız. Süreç aşağıda gördüğünüz gibi olacaktır.
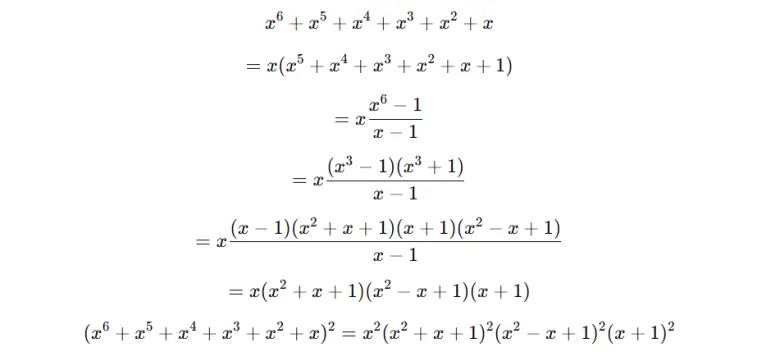
Bu çarpanları uygun biçimde iki gruba ayırdığınızda, her biri altı terimli iki farklı polinom elde edersiniz. Bu iki polinom, yüzleri standart olmayan ama toplam dağılımı tam olarak aynı olan iki zarı temsil eder. Sicherman zarlarının varlığı, tamamen bu cebirsel ayrışım sayesinde mümkündür.
Sicherman zarları nasıl yapılır?
Öncelikle boş yüz olmamalıdır. Bu yüzden her iki polinom da mutlaka birer çarpanı içermelidir. Aksi hâlde terimi ortaya çıkar. İkinci olarak her zar altı yüzlüdür. Bu da her polinomun için değerinin 6 olması gerektiği anlamına gelir.
Buradan x=1 için x2+x+1=3 ve x+1=2 olur. Dolayısıyla her polinomun bir tane ve bir tane çarpanı içermesi gerekir. Bu koşulları sağladıktan sonra geriye yalnızca çarpanlarını nasıl paylaştıracağımız kalır. Bu da bize iki olasılık bırakır.
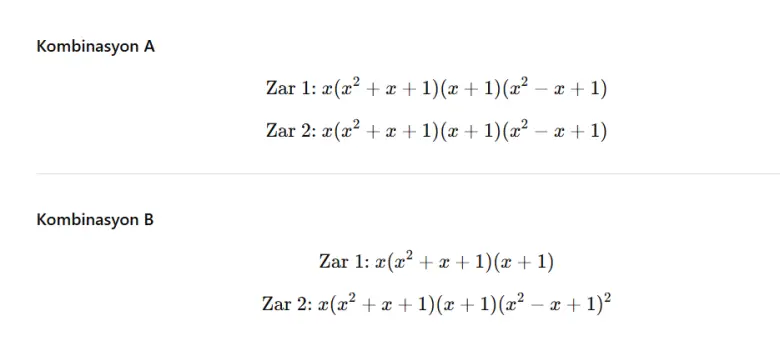
A kombinasyonu bizim standart zar çiftimizi verecektir. Ancak B kombinasyonunu açtığımızda Sicherman zarlarını elde ederiz. Zar 1 polinomu x4+2x3+2x2+x ve Zar 2 polinomu x8+x6+x5+x4+x3+x biçiminde olur ve bu polinomlar doğrudan zar yüzlerini verir.
Sonuçta polinomun üssü bize yüz değerini, katsayısı da o yüzün kaç defa bulunduğunu verecektir. Buna göre birinci zarın yüzleri { 1, 2, 2, 3, 3, 4} ve ikinci zarın yüzleri { 1, 3, 4, 5, 6, 8} biçiminde olur.
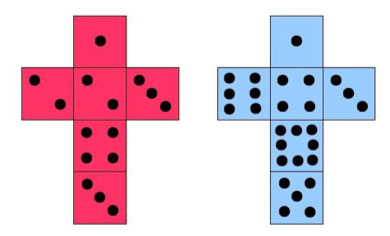
Bu zarların karşılıklı yüzlerinin toplamları sırasıyla 5 ve 9’dur. Bu iki değerin ortalaması 7 eder ve bu sayı, standart bir zarda karşılıklı yüzlerin toplamına eşittir. Ayrıca amaçlandığı gibi, bu zar çiftiyle elde edilen toplamların olasılık dağılımı, iki sıradan zarla elde edilen dağılımla tamamen aynıdır.
Sonuç Olarak
Bu yaklaşım yalnızca Sicherman zarlarıyla sınırlı değildir. Kısıtlar değiştirildiğinde, aynı yöntemle başka zar çiftleri de üretilebilir. Örneğin boş yüzlere izin verilirse, çarpanı üzerinde yapılan düzenlemelerle yeni çözümler ortaya çıkar.
Zarların altı yüzlü olması da şart değildir. Platonik cisimler kullanılabilir ve genel olarak yüz sayısı arttıkça geçerli zar çiftlerinin sayısı da artar.
Problem daha da genişletilebilir. Aynı yöntem üç zar için uygulanabilir mi? Ya da daha genel bir ifadeyle, herhangi bir olasılık dağılımı için onu üreten zarlar her zaman bulunabilir mi? Bu sorular, konuyu doğrudan cebir ve olasılığın temel sınırlarına taşır. Bu nedenle, pratikte çok bir işe yaramasa da, Sicherman zarları matematikçilerin sevdiği oyun araçlarından biridir.
Kaynaklar ve ileri okumalar
- Nishiyama, Yutaka. (2012). Sicherman Dice: Equivalent Sums with a Pair of Dice. International Journal of Pure and Applied Mathematics. 81.
- Let ’em roll. Kaynak site: Plus Math: Yayınlanma tarihi: 10 Temmuz 2006. Bağlantı: Let ’em roll
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel