Schrödinger denklemi bir kuantum durumunun zaman içinde nasıl değiştiğini açıklar. Bu güçlü denklemdeki terimlerin fiziksel anlamını kavramak, kuantum dalga fonksiyonlarının davranışını anlamaya hazırlık sağlar.
İnsanlar maddenin en küçük ölçeklerini düşünmeye başladığında, örneğin bir atom çekirdeğinin çevresinde dönen elektronlara baktıklarında, işlerin garipleştiğini ve Newton yasalarının artık geçerli olmadığını fark ettiler.
Bu küçük ölçeği tanımlamak için yirminci yüzyılın başında geliştirilen kuantum mekaniğine ihtiyaç duyarız. Bu kuramın temel denklemi, Newton’un ikinci yasasının kuantumdaki karşılığı olan Schrödinger denklemidir.
Klasik mekaniğe göre bir fiziksel sistemi konum ve momentumla tanımlarız. Bilardo toplarıyla dolu bir masa düşünün. Bir anda her topun konumunu ve momentumunu yani kütle ile hızın çarpımını biliyorsanız, sistem hakkında bilinmesi gereken her şeyi o an için bilirsiniz.
Ancak kuantum mekaniğinin tanımlamaya çalıştığı nesneler küçük bilardo topları gibi davranmaz. Bazen onları parçacık olarak değil dalga olarak düşünmek daha uygundur. Örneğin ışığı ele alalım. Newton ışığı parçacıklarla açıklamaya çalıştı. Daha sonra, ışığın aslında dalgalarla tanımlandığını gördük.

Işığın bu ikili davranışından ilham alan genç Fransız fizikçi Louis de Broglie önemli bir adım attı: Sadece ışığın değil, maddenin de dalga-parçacık ikiliği gösterdiğini ileri sürdü.
De Broglie’nin 1920’lerde ortaya attığı fikir deneysel kanıtlara değil, Einstein’ın görelilik kuramından esinlenen kuramsal bir sezgiye dayanıyordu. Ancak deneysel doğrulama çok gecikmedi. Dalga-parçacık ikiliğinin en ünlü gösterimi çift yarık deneyidir.
Schrödinger Denklemi Neyi Tanımlar?
Schrödinger, de Broglie’nin bıraktığı yerden devam etti: Her parçacık dalga benzeri bir davranış sergiler. Bu, başlamak için son derece güçlü bir ilkedir fakat şu soru ortada kalır: Bu dalga nasıl matematiksel bir dille ifade edilir ve zaman içinde nasıl evrilir? Daha yalın biçimde: Dalga denklemi nedir?
Klasik mekanikte dalgalar matrisler ve diferansiyel denklemlerle tanımlanır. Schrödinger cesur bir adım atarak bu denklemleri tek bir kuantum parçacığının özelliklerini tanımlamakta kullandı. Bu sayede, Yunanca psi (ψ) harfiyle gösterilen bir dalga fonksiyonu tanımladı.
Bu dalga fonksiyonu, titreşen bir telin dalga fonksiyonuna benziyordu. Telin belirli bir anda ve belirli bir noktadaki sapmasını tanımladığı gibi, kuantum parçacığının durumunu da tanımlıyordu.
Ancak mevcut kuramlarla uyum sağlamak için Schrödinger’ın klasik dalga denklemlerinde bazı temel değişiklikler yapması gerekti. İlk önemli değişiklik, kuantum dalga fonksiyonu için gerçek sayılar yerine karmaşık sayılar kullanmasıydı. Sonuçta ortaya çıkan denklem yalnızca devrim niteliğinde değildi. Aynı zamanda şaşırtıcı bir biçimde matematiksel bir estetik de taşıyordu.
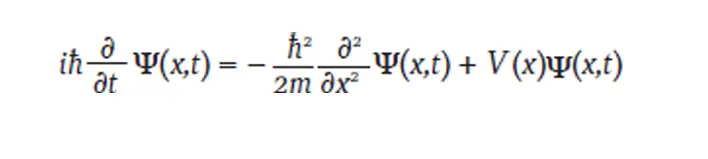
- i: −1’in karekökü, yani sanal birim.
- ħ: Planck sabitinin 2π’ye bölünmesiyle elde edilen azaltılmış Planck sabiti.
- Ψ(x,t): Dalga fonksiyonu. Uzayın her noktasına ve her ana karmaşık bir değer atar.
- ∂/∂t: Dalga fonksiyonunun zamana göre türevi, yani zamanla nasıl değiştiği.
- m: Parçacığın kütlesi.
- ∂²/∂x²: Dalga fonksiyonunun konuma göre ikinci türevi.
- V(x): Dış potansiyel. Bir sistemin x konumundaki potansiyel enerjisini temsil eder.
Schrödinger Denklemi Bir Çok Tuhaflığın Ortaya Çıktığı Yerdir
Schrödinger denklemiyle birlikte her şey değişti. Bu denklem, elektron orbitallerini ve bu orbitallere karşılık gelen enerjileri hesaplamamızı sağlar. Fakat Schrödinger denkleminin yetenekleri bununla sınırlı değildir. Zamanla değişen yani durağan olmayan durumların nasıl evrildiğini de tanımlar.
Farklı orbitallerin süperpozisyonunda bulunan bir elektronun zaman içindeki davranışını bu denklemle açıklayabiliriz. Işığın elektronlarla nasıl etkileştiğini ve elektronların birbirleriyle nasıl etkileştiğini de yine Schrödinger denklemiyle hesaplarız. Kısacası bu denklem bambaşka bir çağın başlangıcı oldu.

Bu olasılıksal bakış açısı, sarsıcı bir sonuçla birleşir. Werner Heisenberg 1927’de hareket eden bir parçacığın konumunu ve momentumunu aynı anda istediğimiz kesinlikle ölçemeyeceğimizi keşfetti. Birini ne kadar hassas bilmek isterseniz, diğeri hakkında o kadar az şey söyleyebilirsiniz. Bu durum ölçüm aracının kusurundan kaynaklanmaz; doğanın temel bir belirsizliğidir.
Bu sonuç bugün Heisenberg’in belirsizlik ilkesi olarak bilinir ve kuantum mekaniğinin tuhaflığını anlatmak için sık sık anılır. İlkenin anlamı şudur: Kuantum mekaniğinde bir parçacığın tam konumundan ya da izlediği kesin bir yolun varlığından söz edemeyiz.
Schrödinger denklemine giriş yapan birçok popüler kuantum fiziği kitabı, denklemi “türetmek” için çeşitli yollar sunar. Ancak bu kitapların yazarları her zaman aynı noktayı vurgular: Bu yöntemlerin hiçbiri denklemi gerçekten birinci ilkelerden çıkarmaz. Richard Feynman’ın dediği gibi, “Onu bildiğiniz herhangi bir şeyden elde etmek mümkün değildir; denklem Schrödinger’in zihninden doğmuştur.”
Sonuç Olarak
Denklemin ilk büyük başarısı, kuantum mekaniğinin doğuşunda kilit rol oynayan hidrojen atomunun ayrık enerji düzeylerini açıklamasıydı. 1913’te Niels Bohr elektronların ancak belirli enerji düzeylerinde bulunabileceği fikrini ortaya attı. Schrödinger denklemini hidrojen atomuna uyguladığında çözümler tam olarak Bohr’un öngördüğü enerji düzeylerini verdi.
Bu başarılar ve çok sayıda deneysel doğrulama sayesinde Schrödinger denklemi, kuantum mekaniği için Newton’un ikinci yasasının yerine geçen temel denklem haline geldi.
Kaynaklar ve ileri okumalar:
- Bird, Jordan & Ekárt, A. & Faria, Diego. (2020). On the effects of pseudorandom and quantum-random number generators in soft computing. Soft Computing. 24. 10.1007/s00500-019-04450-0.
- Schrödinger’s Cat Experiment and the Conundrum That Rules Modern Physics. Yayınlanma tarihi: 5 Mayıs 2021. Kaynak site: Discover Magazine. Bağlantı: Schrödinger’s Cat Experiment and the Conundrum That Rules Modern Physics./
- Schrödinger’s equation — what does it mean?. yayınlanma tarihi: ‘ Ağustos 2012; Kaynak site: Plus Math. Bağlantı: Schrödinger’s equation — what does it mean/
Matematiksel






Schrödinger’in kedisi deneyi sadece bir düşünce deneyidir. Gerçekten yapılmış bir deney değildir. Sanki gerçekten yapılmış bir deney gibi anlatmışsınız.
Yazı “tüm zamanların en etkili düşünce deneylerinden birisini tasarlamışlardı. Bu düşünce deneyi günümüzde Schrödinger’in Kedisi olarak isimlendiriliyor. ” biçiminde başlıyor. Galiba gözünüzden kaçmış.