Okullarda öğrendiğimiz temel geometri kavramları, genellikle düz bir kâğıt yüzeyinde geçerlidir. Ancak şimdi, düz bir kâğıt yerine bir silindir ya da küre gibi eğri bir yüzeye sahip bir kâğıdınız olduğunu hayal edin. Eğri yüzeyler üzerinde çalışmak, düz yüzeylere kıyasla daha karmaşıktır. Bu tür yüzeyleri inceleyen geometri dalına Riemann geometrisi denir.
Einstein, Uzay-Zaman ve Riemann Geometrisi
1915 yılında Albert Einstein, genel görelilik teorisini ortaya koyarak uzayın yalnızca fiziksel olayların gerçekleştiği bir arka plan olmadığını, bu olayların doğrudan bir parçası olduğunu gösterdi. Üç boyutlu uzaya zamanı da ekleyerek dört boyutlu bir uzay-zaman kavramı geliştirdi.
Einstein’a göre kütleçekimi, uzayda yayılan görünmez bir kuvvet değil; kütleli cisimlerin uzay-zaman dokusunu eğip bükmesiyle ortaya çıkan bir etkidir. Bu etkiyi açıklamak için genellikle bir trambolin üzerindeki bowling topu benzetmesi kullanılır. Top, yüzeyde bir çukur oluşturur; yakından geçen küçük cisimler bu eğriliğe kapılarak yön değiştirir. Uzay-zaman da benzer şekilde bükülür ve çevresindeki cisimleri etkiler.

Einstein’ın uzay, zaman, madde ve kütleçekimini birleştiren bu yaklaşımı çığır açıcıydı. Ancak bu teorinin matematiksel temelini kendisi değil, ondan önce gelen matematikçiler atmıştı.
Gauss ve öğrencisi Bernhard Riemann, 19. yüzyılda bir yüzeyin eğriliğini, onu başka bir uzaya yerleştirmeye gerek kalmadan, doğrudan kendi içinde ölçmenin yollarını geliştirmişti. Bu yaklaşım, Einstein’ın uzay-zamanın yapısını tanımlamak için tam da ihtiyaç duyduğu şeydi.
Riemann Geometrisi Nedir?
Yüzeylerden bahsettiğimizde, aslında yerel olarak düz görünen yapılardan söz ederiz. Okulda öğrendiğimiz düzlem geometrisi de bu tür yapılar üzerine kuruludur. Bir küre bile bu tanıma uyar; her ne kadar küresel bir yüzeyde yaşıyor olsak da, bu yüzey bize yerel olarak düz görünür.
Bir yüzeyin küçük bir parçasını düzleme aktarmak, matematiksel olarak bir fonksiyon aracılığıyla yapılır. Bu tür eşlemelere harita adı verilir. Haritalar, yüzeyin sınırlı bölgelerini alıp onları düz bir zemin üzerinde temsil eder. Burada önemli olan, eşlemenin sürekliliği ve tersinin de tanımlı olmasıdır. Yani yüzeyin bir parçası ile düzlemin bir bölgesi arasında kesintisiz ve çift yönlü bir ilişki kurulmalıdır.
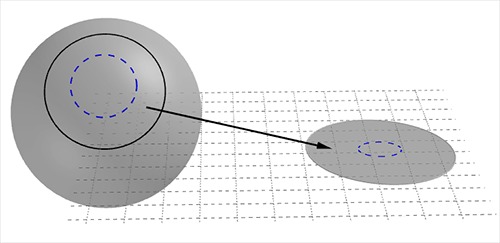
Yüzeyin tamamını tanımlamak için tek bir harita yeterli olmaz. Bunun yerine, yüzeyi parça parça örten birden fazla harita gerekir. Bu haritaların birbirini kısmen örtmesi ve birlikte tüm yüzeyi kapsaması şarttır. Bunu eski harita kitapları gibi düşünebiliriz: Tüm sayfalar bir araya geldiğinde dünya haritası tamamlanır.
Ancak burada önemli bir nokta vardır: Bir yüzeyi tanımlamak için onu çevreleyen üç boyutlu bir uzaya ihtiyaç duymayız. Haritalar, yüzeyin yalnızca kendi iç yapısına dayanır. Oysa biz, yüzeyleri düşünürken genellikle onları uzayda konumlandırır ve zihnimizde bir şekil olarak canlandırırız. Ancak matematiksel olarak, bu dış uzaya gerek kalmadan da yüzeyi tam anlamıyla tanımlamak mümkündür.
Yine de bu yaklaşımda hâlâ eksik bir şey vardır: Yüzey üzerinde açıları ve uzaklıkları nasıl ölçeceğimizi bilmiyoruz. Çünkü bu kavramları dış uzaydan alamayız; onları yüzeyin kendi yapısı içerisinde tanımlamamız gerekir.
İşte bu noktada Riemann yüzeyleri devreye girer. Bu yüzeyler, yalnızca topolojik yapı değil, aynı zamanda açı ve mesafe ölçmeyi mümkün kılan ek bir yapıyla birlikte tanımlanır. Riemann’ın geliştirdiği Riemann metrikleri, herhangi bir dış mekâna ihtiyaç duymadan bir yüzeyin üzerine mesafe ve açı ölçüsü yerleştirmemizi sağlar.
İki Riemann yüzeyi ne zaman “aynı” olur?
Bazı türdeki yüzeyleri sınıflandırmanın şaşırtıcı derecede düzenli bir yolu vardır. Bunun için mesafe ya da açı gibi klasik geometrik kavramları bir kenara bırakıp, yüzeyleri kesip yapıştırmadan; yalnızca esnetip bükerek şekil değiştirmeye izin vermek gerekir. Bu yaklaşım, topolojik bakış açısını temsil eder.

Eğer bir yüzey, bu tür dönüşümlerle başka bir yüzeye dönüştürülebiliyorsa, bu iki yüzey topolojik olarak eşdeğer kabul edilir. Bu perspektifle bakıldığında, çoğu yüzey aslında birkaç temel örneğe indirgenir. Bunlardan biri küredir. Diğerleri ise deliği olan simit benzeri yüzeylerdir: bir delikli simit, iki delikli simit, üç delikli simit… Bu şekilde artarak devam eder.
Benzer şekilde, iki Riemann yüzeyinin “aynı” sayılabilmesi için yalnızca şekil olarak benzemeleri yeterli değildir; açıların da korunması gerekir. Bu durumda, yüzeylere izomorfik denir. Ancak her topolojik eşdeğerlik, izomorfluk anlamına gelmez. Yani iki yüzey şekil olarak birbirine benzese de, biri diğerine dönüştürülürken açılar değişiyorsa, artık Riemann yüzeyi olarak aynı sayılmazlar.
Riemann yüzeyleriyle ilgili bir diğer önemli nokta ise düzlemin kendisidir. Karmaşık sayılar, gerçek sayıların bir uzantısıdır ve doğaları gereği iki boyutludur. Gerçek sayılar bir doğru oluştururken, karmaşık sayılar bir düzlem meydana getirir.
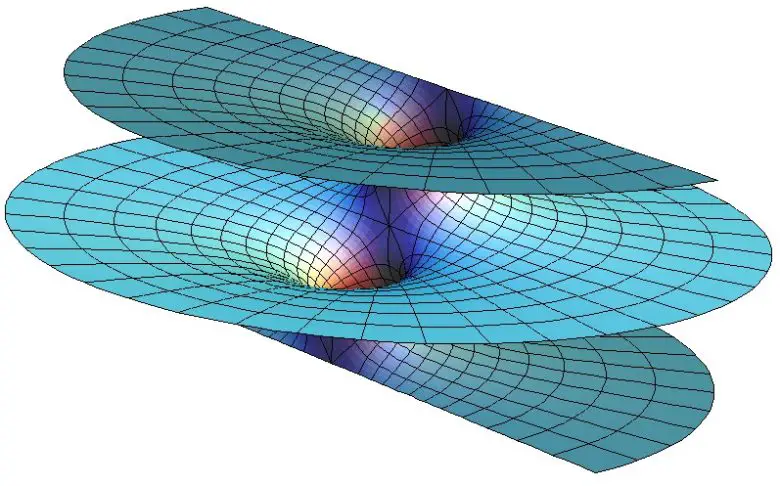
Topolojik açıdan bakıldığında, bu sıradan bir düzlemdir. Ancak karmaşık sayılar, bu düzleme fazladan bir matematiksel yapı kazandırır. Bu yapı sayesinde, düzlem üzerinde tanımlanan fonksiyonların özellikleri kısıtlanır. Yani her fonksiyon bu düzlemde “uygun” şekilde çalışmaz. İşte bu kısıtlama, Riemann yüzeylerini özel kılan şeylerden biridir; yalnızca geometrik değil, aynı zamanda analitik bir yapıya da sahiptirler.
Kaç farklı Riemann yüzeyi vardır?
Burada “farklı”dan kastımız, birbirine izomorfik olmayan, yani açısal yapıları korunarak birbirine dönüştürülemeyen yüzeylerdir. Deliklerin, yüzeylerin topolojik sınıflandırılmasında önemli bir rol oynadığını biliyoruz. Bu nedenle, önce hiç deliği olmayan Riemann yüzeylerine bakalım. Ayrıca, bu yüzeylerin sonsuza uzanmamasını ve kenarlarının bulunmamasını şart koşalım. Yani matematiksel olarak yalnızca kapalı Riemann yüzeylerini ele alacağız.
Bu tanıma göre, bir küre bu yüzey türüne örnek olur. Topolojide, kapalı, yönlendirilebilir ve tek parça olan, deliği olmayan her yüzey, topolojik olarak bir küreye denktir. Riemann yüzeyleri için de benzer bir durum geçerlidir.

Tüm kompakt (yani kapalı ve sınırlı) Riemann yüzeyleri, eğer delikleri yoksa, Riemann küresi adı verilen özel bir yüzeye izomorfiktir. Bu durumda, deliksiz tüm kompakt Riemann yüzeyleri aslında aynı analitik yapıyı paylaşır.
Peki ya delikli yüzeyler? Örneğin, tek delikli bir yüzey, yani bir simit. Topolojik açıdan bakıldığında, kalın bir simitle ince bir simit arasında fark yoktur; ikisi de aynı yapıdadır. Ancak Riemann yüzeylerinde durum farklıdır. Burada yalnızca şekil değil, açılar da önem taşır. Kalın bir simidi esnetip incelttiğinizde, açıları da değiştirmiş olursunuz. Bu da yüzeyin Riemann yapısını bozar.
Yani bazı yüzeyler, topolojik olarak tamamen aynı görünse de, Riemann yüzeyi olarak farklıdır. Bu durumda artık izomorfik sayılmazlar. Peki, bu farkı nasıl anlarız?
Bu sorunun cevabı, Riemann yüzeylerinin en etkileyici yönlerinden birine açılır. Yüzeyin geometrik yapısını anlamak için onu düzleştirip açarız. Böylece her Riemann yüzeyini yalnızca topolojik değil, aynı zamanda geometrik ve analitik açıdan da sınıflandırmak mümkün olur.
Sonuç olarak
Riemann geometrisi, düz olmayan yüzeylerin ve çok daha genel yapıların derinlemesine anlaşılmasını sağlayan güçlü bir matematiksel çerçevedir. Bugün, Riemann yüzeyleri ve moduli uzayları gibi kavramlar sayesinde hem matematikçiler hem de fizikçiler, çok boyutlu evrenlerin, kuantum alanlarının ve sayıların derin yapıları üzerine daha kapsamlı bir anlayış geliştirebiliyorlar. Bu nedenle, Riemann geometrisi, yalnızca soyut bir teori değil, aynı zamanda evrenin nasıl işlediğine dair elimizdeki en güçlü araçlardan biridir.
Kaynaklar ve İleri Okumalar:
- A.L. Audichya; Mathematics: Marvels and Milestones; ISBN: 8189473409
- Moduli spaces: Introducing Riemann surfaces. Yayınlanma tarihi: 3 Temmuz 2024. Kaynak site: Plus Math. Bağlantı: Moduli spaces: Introducing Riemann surfaces
Matematiksel