Ramanujan Kökleri İle Şaşırtıcı Sonuçlar Elde Edebilirsiniz

Ünlü matematikçiler hakkında pek çok kitap yazılmıştır. Ancak çok azı, yaşam öyküleriyle tam uzunlukta bir filme konu olacak kadar övgü toplamıştır. Srinivasa Ramanujan’ın hayatını anlatan film ise bu nadir istisnalardan biridir. Günümüzde kendisi, pek çok şeyin yanı sıra “Ramanujan Kökleri” ile de anımsanmaktadır.

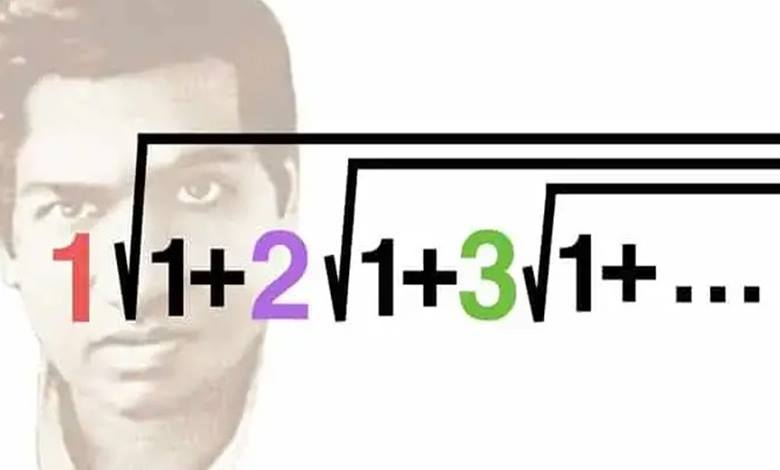
Srinivasa Ramanujan, 22 Aralık 1887’de, Hindistan’da fakir bir ailede doğdu. Üç kardeşi doğumlarından sonraki bir yıl içinde öldüğü için tek çocuk olarak büyüdü. On bir yaşında üniversite düzeyinde matematik bilgisine ulaşmıştı.

On üç yaşında kendi matematiksel fikirlerini geliştirmeye başlamıştı. Kısa süre içinde matematik alanındaki başarılarıyla ödüller aldı ve özellikle geometri ile sonsuz serilere ilgi duydu.

1903 yılında, henüz on altı yaşındayken Ramanujan, G. S. Carr’ın saf ve uygulamalı matematikte beş bin teoremi derlediği kitabını kütüphaneden edindi. Bu kitabın, onun matematiksel dehasının ortaya çıkışında belirleyici bir rol oynadığı kabul edilir. Kuramsal matematiği ilk kez bu kaynaktan öğrenen Ramanujan, belki de bu nedenle yaşamı boyunca ispat yapma ihtiyacı duymadı.

1904’te Kumbakonam’daki Government Arts College’a girdi ve matematikte olağanüstü bir başarı gösterdi; ancak diğer derslere karşı hiçbir ilgi göstermedi. Bu ilgisizlik, 1905 yılında okulu bırakmasına ve evden ayrılmasına yol açtı. Daha sonra Madras’taki Pachaiyappa’s College’a kaydoldu, fakat burada da durum değişmedi.

Sonunda, diplomasını almadan okuldan ayrıldı ve tüm enerjisini matematik araştırmalarına yöneltti. Yeteneği ancak 1910’da fark edildi. Hindistan Matematik Cemiyeti’nin kurucusu Profesör Ramaswami, Ramanujan’ı Madras Üniversitesi’ne araştırmacı olarak kazandırdı.

Ramanujan Sonsuzlukla Nasıl Oynadı?

1911 yılında, Hintli matematik dehası Srinivasa Ramanujan, aşağıdaki problemi Journal of the Indian Mathematical Society dergisinde yayımladı. Aylarca bir çözüm bekledi; ancak kimse yanıt vermeyince, çözümü kendisi sundu. Sorduğu soru şuydu: Aşağıdaki denklemin değeri nedir? Dikkat çekici bir şekilde, yanıt tam olarak 3’tü.

Ramanujan’ın sorusunun cevabına geçmeden önce, kendisinin sonsuzlukla nasıl oynadığına dair bir fikir edinelim. Öncelikle aşağıdaki temel eşitliği ele alalım.

x = \sqrt{x\sqrt{x^{2}}}

Çoğumuz bu eşitliği kabul etmekte zorlanmayız. Ancak bu ifade, uygun bir yineleme fikriyle ele alındığında, çok daha dikkat çekici yapılar ortaya çıkar. Örneğin $x^{2}$ yerine her adımda $x\sqrt{x^{2}}$ yazıldığında, ifade iç içe geçen kökler hâlini alır ve şu biçimde devam eder:

x = \sqrt{x\sqrt{x\sqrt{x\sqrt{x\sqrt{x\cdots}}}}}

Bu yaklaşım belirli sayılar için somut örnekler de üretir. Örneğin:

2 = \sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{2\cdots}}}}}

Daha da ileri gidildiğinde, benzer bir yineleme fikri küpkökler için de uygulanabilir ve şu tür ifadeler elde edilir:

x = \sqrt[3]{x^{2}\sqrt[3]{x^{2}\sqrt[3]{x^{2}\cdots}}}

Böylece son derece sıradan görünen bir eşitlikten, sezgisel ama alışılmadık köklü özdeşlikler türetmek olasıdır. Mesela aşağıdaki sonucu elde edebiliriz.

2 = \sqrt[3]{4\sqrt[3]{4\sqrt[3]{4\sqrt[3]{4\cdots}}}}

Ramanujan Kökleri Nedir?

Bu tür özdeşlikler ilk bakışta şaşırtıcı görünse de, arkasında oldukça basit cebirsel ilişkiler yer alır. Şu ifadeyle başlayalım: $(x + 1)^2 = x^2 + 2x + 1 = x(x + 2) + 1$

Terimleri yeniden düzenlediğimizde şu biçimi elde ederiz:

$(x + 1)^2 = 1 + x(x + 2)$

Şimdi bu eşitlikte $x$ yerine sırasıyla 2, 3 ve 4 yazalım:

$3^2 = 1 + 2(4), \quad 4^2 = 1 + 3(5), \quad 5^2 = 1 + 4(6), \ \ldots$

Bu denklemlerin her iki tarafının karekökünü aldığımızda şu sonuçlara ulaşırız:

$3 = \sqrt{1 + 2(4)}$ $4 = \sqrt{1 + 3(5)}$ $5 = \sqrt{1 + 4(6)}$ $6 = \sqrt{1 + 5(7)}$

Birinci denklemdeki $4$ ifadesini, ikinci denklemin sağ tarafıyla değiştirirsek şu sonucu elde ederiz:

$3 = \sqrt{1 + 2\sqrt{1 + 3(5)}}$

Şimdi aynı işlemi bir adım daha ileri götürelim. Yukarıdaki ifadede yer alan 5 sayısını, üçüncü denklemin sağ tarafıyla değiştirelim.

$3 = \sqrt{1 + 2\sqrt{1 + 3\sqrt{1 + 4(6)}}}$

Bu durumda ifadesine ulaşırız. Aynı yöntemi bir sonraki denklem için de uyguladığımızda yapı daha da belirginleşir:

$3 = \sqrt{1 + 2\sqrt{1 + 3\sqrt{1 + 4\sqrt{1 + 5(7)}}}}$

Bu noktada örüntü açığa çıkar. Parantez içindeki son tam sayı, her adımda bir sonraki denklemin sağ tarafı ile değiştirilebilir. Bu işlem, aynı mantıkla sonsuza kadar devam eder ve bize aşağıdaki sonucu verir.

$3 = \sqrt{1 + 2\sqrt{1 + 3\sqrt{1 + 4\sqrt{1 + 5\sqrt{\cdots}}}}}$

Sonuç Olarak

Ramanujan, üç değişken kullanan genel bir ifade elde ederek bu tür eşitliklerin sonsuz sayıda örneğini üretmiştir. Ancak bu ifadenin matematiksel olarak tam anlamıyla kanıtlanabilmesi, yakınsak olduğunu göstermeyi gerektirir ki bu, çok daha karmaşık bir meseledir. Bu resmî kanıt, Ramanujan’s Route to Roots of Roots başlıklı belgede yer almaktadır.

Kaynaklar ve ileri okumalar:

Solution: ‘Puzzles Inspired by Ramanujan’; yayınlanma tarihi: 8 Ağustos 2016; Kaynak site: Quanta Magazine. Bağlantı: Solution: ‘Puzzles Inspired by Ramanujan’
Kusniec, Charles. (2025). On Generalized Ramanujan-Style Nested Radicals for All Integers. 10.5281/zenodo.16293629.
Rao, K. & Berghe, G.. (2005). On an entry of Ramanujan in his Notebooks: A nested roots expansion. Journal of Computational and Applied Mathematics – J COMPUT APPL MATH. 173. 371-378. 10.1016/j.cam.2004.04.009.

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel

Etiketler