Günümüzde sayılardan söz edildiğinde çoğu kişinin aklına, günlük hayatta kullanmaya alışık olduğumuz doğal sayılar ya da tam sayılar gelir. Oysa sayı teorisi gibi alanlarda çalışıldığında, bu alışıldık sayıların ötesine geçen, çok daha farklı biçimde işleyen sayı sistemlerine ihtiyaç duyulur. P-adik sayılar da bu türden, sezgilerimizi zorlayan ama matematiksel açıdan son derece güçlü bir sayı sisteminin örneğidir.

Matematik çoğu zaman örüntüleri ortaya çıkarmakla ilgilidir. Örneğin topolojinin bazı alanları düğümlerin ya da geometrik şekillerin sınıflandırılmasıyla uğraşırken, sayı teorisi asal sayıların dağılımı gibi özellikleri inceler.
İlişkileri biraz daha basit bir düzeyde ele aldığımızda ise, Babillilerin binlerce yıl önce fark ettiği 5 ve 6 sayılarıyla ilgili ilginç bir örüntüyle karşılaşırız. 5’in karesi 25’tir ve 5 ile biter; 25’in karesi 625’tir ve 25 ile biter; 625’in karesi ise 390.625’tir ve 625 ile biter.
6 sayısıyla oynadığınızda ortaya çıkan sonuçlar 5 kadar çarpıcı olmasa da burada da bir örüntü görülür. 6’nın karesi 36’dır; 36’nın karesi ise 1.296 eder. Bu kez 36 sayı dizisinin içinde aynen görünmez, ancak sonuç her zaman 6 ile biter. Bu durum, matematiğin en önemli ve aynı zamanda en tuhaf sayı sistemlerinden birine açılan kapıdır.
Otomorfik Sayılar Nedir?
Genel olarak, karesi kendisiyle aynı rakam ya da rakamlarla biten sayılara otomorfik sayılar denir. İlginçtir ki 0 ve 1 dışındaki tüm otomorfik sayılar ya 5 ya da 6 ile biter.
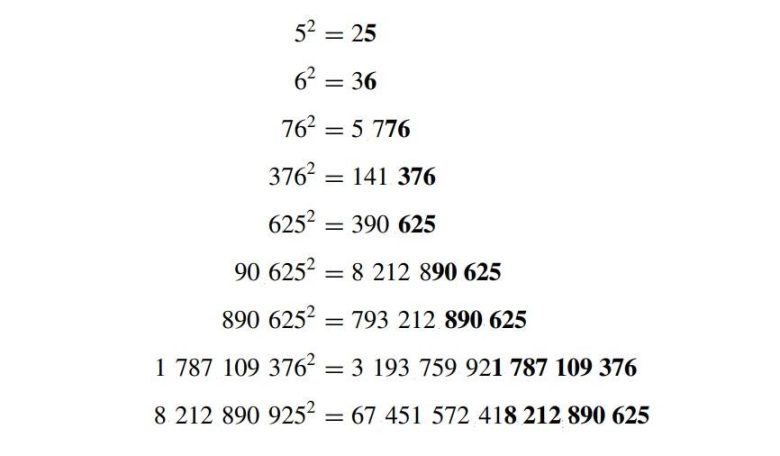
Bununla birlikte 5 sayısı özellikle dikkat çekicidir. 5 yalnızca otomorfik olmakla kalmaz; karesi de otomorfiktir, karesinin karesi de.
Aslında örüntü, üçüncü kareden sonra bozuluyor gibi görünür: 390.625’in karesi 152.587.890.625 eder. Bu nedenle 390.625 otomorfik değildir, çünkü sayı, karesinin sonunda bütünüyle yer almaz. Ancak son beş basamak karesinin sonunda yer alır. 90.625 sayının karesi alındığında 8.212.890.625 sonucu elde edilir. Demek ki 90.625 de otomorfik bir sayıdır.
Aslında bu işlem sonsuza kadar sürer. Sonunda ortaya çıkan şey, bütünüyle otomorfik olan, yani karesi yine kendisine karşılık gelen sonsuz büyüklükte bir sayıdır (başka bir deyişle koşulunu sağlayan sonsuz bir sayı). Bu sonsuz sayının tamamını yazmak mümkün olmasa da, son basamakları bilinmektedir: …918.212.890.625.
Böyle bir “sabit nokta”nın sonsuzda var olması başlı başına şaşırtıcıdır. Bu sayının en azından son basamaklarının tam olarak belirlenebilmesi ise daha da şaşırtıcıdır. Bu noktada da işin içinde P-adik sayılar girer.
P-adik sayılar nedir ve otomorfik sayılarla ne ilgisi vardır?
Alışık olduğumuz ondalık sayılarda sonsuzluk, ondalık noktasının sağında yer alır. Örneğin π = 3,14159… gibi sayılar bu yüzden sağa doğru uzar. Ancak p-adik sayılarda ise durum tersinedir. Yani sayı, sola doğru sonsuza kadar devam eder. Bu ilk bakışta garip görünse de, p-adik sayılar da düzenli bir matematiksel yapı oluşturur. Bu sayede de üzerinde aritmetik işlemler yapılabilir.
Bu sayı sistemi, otomorfik sayılarla karşılaşınca anlam kazanmaya başlar. Ondalık sistemde otomorfik sayılar, karesi alındığında kendi son basamaklarıyla biten sayılardır. Ancak bu örüntü, sıradan gerçek sayılar içinde bir noktada bozulur. Az öncede gördüğümüz gibi, sayı bütünüyle karesinin içinde yer almaz.

P-adik sayılar, tam olarak bu “son basamakları koruma” fikrini ciddiye alır. Bu yüzden 390.625 bütünüyle otomorfik olmasa bile, son basamakları korunarak daha uzun otomorfik yapılar üretilebilir. Böylece …90.625, …8.212.890.625 gibi giderek büyüyen otomorfik sayılar ortaya çıkar. Bu süreç, p-adik dünyada bir sınıra, yani n² = n eşitliğini sağlayan bir “sabit noktaya” yaklaşır.
Bu noktada alışık olduğumuz kurallar kırılır. Gerçek sayılarda n² = n denklemi yalnızca n = 0 veya n = 1 için geçerlidir. p-adik sayılarda ise …890.625 gibi ne 0 ne de 1 olan sayılar da bu denklemi sağlayabilir. Bunun nedeni, p-adik sistemlerde sıfır olmayan sayıların çarpımının sıfır olabilmesidir. Bu tür sayılara “sıfır bölen” denir ve bunlar bazı hesaplamaları sorunlu hâle getirir.
Bu sorunların kaynağı, kullanılan tabandır. Burada anlatılan örnekler aslında 10-adik sayılardır. Ancak 10 asal bir sayı değildir ve bu yüzden sıfır bölenler ortaya çıkar. Bu nedenle p-adik sayıların asıl tanımı, p’nin asal bir sayı olması koşuluna dayanır. Örneğin 3-adik sayılar, 3 tabanında tanımlanır ve bu sistemde sıfır bölenler yoktur.
Sonuç olarak
Özetle, otomorfik sayılar p-adik sayıların tuhaflığını ortaya çıkaran bir kapıdır. p-adik sayılar ise, otomorfik sayıların ondalık sistemde yarım kalan davranışını matematiksel olarak tamamlayan daha geniş bir sayı evreni sunar. İlk bakışta anlaşılmaz görünmelerine rağmen, p-adik sayılar sayı teorisinin merkezinde yer alır ve modern matematikte yoğun biçimde kullanılır.
Kaynakla ve ileri okumalar
- Simple Math Creates Infinite and Bizarre Automorphic Numbers. Yayınlanma tarihi: 11 Ocak 2024. Kaynak site: Scientific American. Bağlantı: Simple Math Creates Infinite and Bizarre Automorphic Numbers
- An Infinite Universe of Number Systems. Yayınlanma tarihi: 19 Ekim 2020. Bağlantı: An Infinite Universe of Number Systems
- Fried, Michael. (1980). A Note on Automorphism Groups of Algebraic Number Fields. Proceedings of The American Mathematical Society – PROC AMER MATH SOC. 80. 386-386. 10.1090/S0002-9939-1980-0580989-8.
Matematiksel





