Matematikte hepimizin aşina olduğu kesirler, MÖ 1800’den beri Mısır’da bir bütünün parçalarını ifade etmek için kullanılmıştır. Ancak o dönemde kullanılan kesirler, paydası bir olarak ifade edilen birim kesirler ile sınırlıydı. Yani Eski Mısırlılar 2⁄3 ve 3⁄4 gibi kesirler ile işlem yapmak istediklerinde bunları, örneğin 1⁄3 + 1⁄13 + 1⁄17 biçiminde, birim kesirler cinsinden ifade etmek zorunda kalırdı.
Pratik hesaplamalar için bu yöntem oldukça uzun bir süre işe yaradı. Ancak bu hesaplamalar hem zaman alıcı hem de hata yapmaya müsait idi. Günümüzde kullandığımız ondalık sayılar ( ondalık kesirler de denir) ile bu soruna bir çözüm üretmek isteyen Simon Stevin sayesinde 1585 yılında tanıştık.
Ondalık Sayılar İle Nasıl Tanıştık?
Ancak paydası 10’un katı olan “ondalık kesirler” fikri, Stevin’den önce de biliniyordu. Ondalık işaretinin kullanımı, esasında Sümerler tarafından kullanılmış olan kademeli sayı sistemine dayanır. Bu sisteme dayanarak, bir sayının tam sayı kısmının kesirli kısmından ayrı olarak gösterilmesi geliştirilmiştir.
Ondalık kesirli yazılışında zamanla ondalık paydası yazılmamaya başlanmış ve kesirli kısım değişik yazılışlarla tam sayı kısmından ayrılarak gösterilmiştir. Örneğin M.S. 1400 civarında, Fars matematikçi Gıyaseddin Cemşid bir sayının tam sayı kısmını siyah katranla yazarken, kesirli kısmını kırmızı olarak yazardı.
Ondalık noktasının ilk kullanıldığı kaynak olarak 1492 yılında İtalyan Matematikçi Francesco Pellos’un yazdığı Compendio del Abaco isimli eseri bilinmektedir.
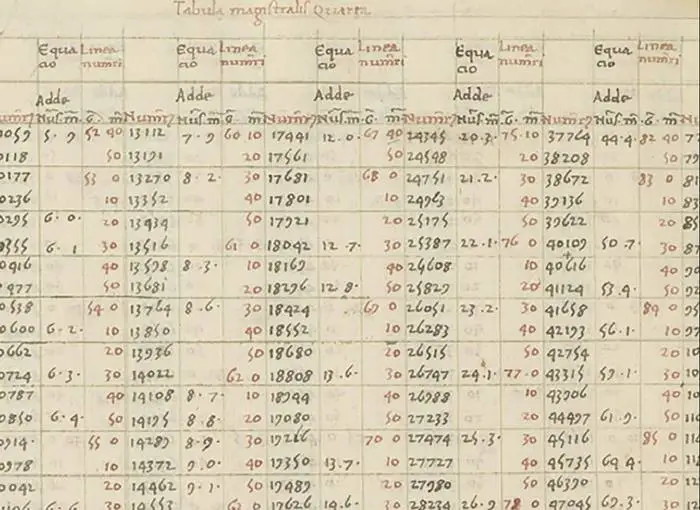
Aslında Simon Stevin’in çalışmaları fikrin Avrupa’da yaygınlaşmasını sağladı. Bu da 1585’te ondalık kesirlerin ve günlük kullanımlarının temel bir açıklamasını sunduğu De Thiende adlı bir kitapçık sayesinde olacaktı.
Ancak o dönemlerde Stevin’ın ortaya attığı gösterim biçimi günümüzdekinden oldukça farklıydı. Aşağıdaki görselde kendisinin 32,567 ondalık sayısını nasıl yazdığını görebilirsiniz.
Yukarıdaki rakama dikkatle bakarsanız aslında sezgisel olarak, kendisinin 32,567 sayısını nasıl gösterdiğini algılayabilirsiniz. Öncelikle elbette bu sayının ondalık açılımını düşünmeniz gerekiyor.
Sayımız 32 + 5/10+ 6/100+7/1000 biçimindedir. 32’nin tamamından sonra 0 gelir, çünkü 32 sayımızın tam kısmıdır. 5 sayısından sonra gelen 1 paydada bir tane sıfır var anlamı taşır. Aynı biçimde 6 sayısından sonra gelen 2 paydadaki iki sıfır, 7 sayısından sonra gelen 3 ise paydadaki üç sıfırı ifade eder. Tüm bunlar onun önerisi ile bir daire içine yazılmıştır.
Ondalık Sayıları Nasıl Göstermeliyiz?
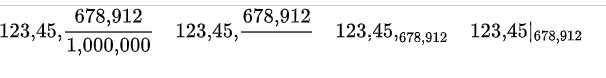
Aslında bu noktadan sonra da işler biraz karışmaya başlar. Sonucunda tarih boyunca matematikçiler tamsayıları ondalık basamaklardan ayırmak için nokta, virgül, ters virgül, dikey çubuk, yatay çizgi, iki nokta üst üste, noktalı virgül ve hatta sıfır dahil her türlü sembolü kullandılar. Yukarıda bunun bazı örneklerini görebilirsiniz. Neyse ki sonunda bir karara vardılar.
Günümüzde bir sayının tam sayı kısmı ile ondalık kısmı arasına yerleştirilen sembole ondalık ayırıcı denir. Stevin’in bir daire içine yazdığı sıfır sayısı daha sonraları ufalarak bir noktaya dönüştü. Devamında bu nokta sayıların arasında orta yükseklikte olacak biçimde kullanılmaya başlandı.
Ancak bir sorun daha vardı. Bu sefer nokta çarpma için kullanılan gösterim biçimi ile karışmaya başlamıştı. Bu sorunu da ortadan kaldırmak için noktanın konumunu biraz aşağı indirmek zorunda kaldık. Ve günümüzde bulunduğu konuma yerleştirdik.
Ancak sorunlar bitmedi. Çünkü ondalık sayılar için kullanılan bu nokta işareti evrensel olarak kabul görmedi. 18. yüzyıl Avrupa kıtasında Fransa’nın etkisiyle günlük kullanımda ve derslerde ondalık işareti olarak virgül yaygınlaşmaya başladı.
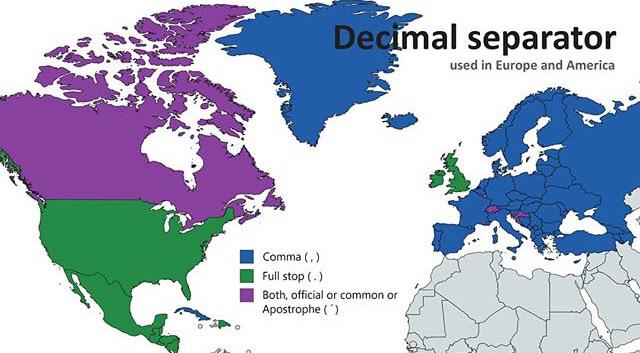
Sonunda dünya ondalık sayıları nokta ile ayıran ülkeler ve virgül ile ayıran ülkeler olarak ikiye bölünecekti. Bu ayrımın nasıl gerçekleştiğini aşağıdaki görselde de görebilirsiniz. Sonucunda günümüzde arasında Türkiye’nin de bulunduğu mavi ile gösterilen ülkelerde ayıraç olarak virgül kullanılır. Yeşil ile gösterilen ülkelerde nokta kullanılır. Mor ile gösterilen ülkelerde de her iki gösterime de rastlanır.
3435246830578457804 biçimindeki bir sayıyı okumak zordur. Bu nedenle sayıyı sağdan sola doğru üçerli olarak gruplamamız gerekir. Sonrasında da her üçlü grubun arasına bir nokta koyarız. Yani aslında sayımızı 3.435.246.830.578.457.804 biçiminde yazarsak daha iyi anlarız.
Ancak bir çok ülke vatandaşı için bu yazış biçimimiz sadece kafa karıştırıcı olacaktır. Sonuçta bu sayıyı eğer İngiltere’de yazsaydınız 3,435,246,830,578,457,804 biçiminde bir anlama sahip olacaktı. Sonuçta bu da yanlıştır.
Nokta mı, Virgül mü Tartışmasına Son Nokta?
Sadece İngiltere değil aslında dünyanın bir çok yerinde ondalık sayıları göstermek için nokta ve sayıları gruplamak için virgül kullanılır. Bu nedenle de konu hakkında bilgisi olmayan birisinin iki farklı gösterim nedeniyle karışıklıklar yaşaması olasıdır.
Bu sorunu çözmek amacıyla 2003 yılında düzenlenen uluslararası bir konferansta bir karar alındı. Bu tarihten itibaren ister nokta ister virgül, ondalık sayıları nasıl gösterirsek gösterelim, sayıları gruplandırmak için herhangi bir işaret kullanılmaması, sadece boşluk bırakılması kabul edildi.
Ayrıca ISO 31-0’a göre çarpım işareti olarak nokta kullanıldığında ondalık işareti olarak da noktanın kullanılmaması gerekmektedir. Son olarak Türkiye’de parasal değerler ifade eden sayılarda üst para birimi ile alt para birimi (örn. Lira ve Kuruş) arasında nokta kullanılmaktadır.
Sonuç Olarak;
Stevin aslında ondalık sayıların kabulünün zaman alacağını öngörmüştü. Gerçekten de onun fikrini ortaya koymasından yaklaşık 200 yıl sonra, Fransız Devrimi sırasında Avrupa’da uzunluk ve ağırlık için ondalık ölçüler kullanılmaya başlandı.
Hatta Fransa bir adım daha ileri gitti ve zamanı ölçmek için de ondalık sayıları kullanmayı önerdi. Yani eğer bu fikir kabul edilseydi günümüzde günde 10 saat, her saatte 100 dakika ve her dakika 100 saniye olacaktı. Neyse ki bir sene sonra vazgeçtiler.
Sonuçta artık hesap makinenize baktığınız zaman neden virgül işareti yerine nokta gördüğünüzün cevabını biliyorsunuz. Ayrıca göz atmak isterseniz: Ispanak, Temel Reis ve Demir Efsanesi Bir Ondalık Sayı Hatası mıydı?
Kaynaklar ve ileri okumalar:
- Resolution 10 of the 22nd CGPM (2003); Symbol for the decimal marker; Bağlantı: https://www.bipm.org/
- History of Decimals and the Metric System; Bağlantı: https://extranet.education.unimelb.edu.au/
- The Maths Book: Big Ideas Simply Explained; Publisher: DK; ISBN: 1465480242
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
