Matematiğin doğasıyla ilgili en temel sorulardan biri şudur: Matematik, insan zihninin bir icadı mı, yoksa evrende başlı başına var olan bir düzenin keşfi mi? Diğer bir deyişle, “Matematik keşif mi, icat mı?”

Bu soru sadece felsefi bir merak değildir. Aynı zamanda bilginin doğasına, öğrenme biçimimize ve bilimin neye dayandığına dair temel meseleleri gündeme getirir. Matematiğin kökenini anlamaya çalışmak, aslında düşünmenin, anlamanın ve anlamlandırmanın kendisini sorgulamaktır
Matematik En Olgun Bilimlerden Biridir
Matematik, bilim dalları arasında en köklü ve en başarılı olanlardan biridir. Bu disiplinin ilk büyük eseri sayılan Öklid’in Elementler adlı yapıtı yaklaşık 2400 yıl önce kaleme alınmış ve yirminci yüzyıla dek matematik eğitiminde temel kaynak olarak kullanılmıştır. Buna karşılık, fiziğin benzer ölçekteki ilk eseri olan Newton’un Principia’sı yalnızca 300 yıl, biyolojinin kurucu metni sayılan Darwin’in Türlerin Kökeni ise yaklaşık 150 yıl önce yazılmıştır.
Özellikle son üç yüzyılda matematik olağanüstü bir gelişim göstermiştir. Bilgiyi bu denli düzenli, sistemli ve kararlılıkla biriktirme konusunda, diğer bilim dalları ona ancak son yüzyılda yaklaşabilmiştir. Ayrıca, matematikte yöntemler konusunda neredeyse evrensel bir uzlaşma hâkimdir. Beklenen şey nettir: Kanıt. Üstelik bir şeyin kanıtlanıp kanıtlanmadığı hususunda genellikle ciddi görüş ayrılıkları yaşanmaz.
Buna karşılık, diğer bilimlerde deneysel sonuçların yorumu ya da bir teorinin diğerine tercih edilip edilmemesi gibi konular sıkça tartışma yaratır. Matematiğin bu açıklığı ve istikrarı, onu diğer bilimlerden ayıran temel özelliklerden biridir.
Ancak tüm başarısına ve kesinliğine rağmen, matematiğin temelleri gizemini korur. Sayılar, kümeler, fonksiyonlar gibi matematiksel varlıkların gerçekten var olup olmadıkları hâlâ tartışmalıdır. Bu varlıklar, fiziksel dünyanın nesnelerinden (sandalyeler, atomlar) ya da zihinsel dünyanın öğelerinden (inançlar, arzular) tamamen farklı bir düzlemde yer alıyor gibidir.
Dahası, bu kavramlar hakkında sadece düşünüp tartışmıyoruz; onları bildiğimizi de iddia ediyoruz. Her doğal sayının yalnızca bir ardılı olduğunu nasıl bilebiliyoruz? Temel bilgileri hangi temele dayanarak doğru kabul ediyoruz?
Tüm bu sorular, bizi şu temel meseleye götürüyor. Eğer matematiksel nesnelerden oluşan bir “üçüncü dünya” varsa, zihinsel ve fiziksel dünyaya sıkı sıkıya bağlı olan biz insanlar, bu başka dünyayla nasıl bağ kurabiliyoruz?
Matematik Keşif mi Ya da İcat mı Tartışması Neden Var?
Yukarıda ele aldığımız sorunlara yanıt olarak, matematik felsefecileri genellikle iki ana yönelimden birine eğilim gösterir. Bazıları matematiği “içimizde” konumlandırır. Bu görüşe göre, matematiksel nesneler bir anlamda bizim yarattığımız varlıklardır. Bu durumda matematik hakkında konuşmak ya da düşünmek, aslında kendimiz hakkında konuşmak ve düşünmektir.
Bu yaklaşıma göre üçüncü bir dünyadan söz etmek gerekmez. Çünkü matematiksel nesneler zaten bizim düşüncelerimizden türemiştir ya da doğrudan onlardan oluşur. Dolayısıyla matematiksel dünya ile bizim dünyamız arasında bir uçurum da yoktur. Arada bir boşluk olmadığında, onu aşmaya da gerek kalmaz.
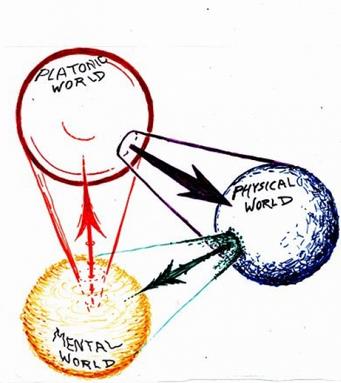
Bazı filozoflar ise matematiği “bizim dışımızda” konumlandırır. Onlara göre matematiksel nesneler, düşüncelerimizden ve duygularımızdan tamamen bağımsız biçimde var olur. Bu görüşe göre, fiziksel dünyayı algıyla kavradığımız gibi, matematiksel dünyayı da zihinsel bir tür “algı” yoluyla kavrayabiliriz. Doğal sayıların dizisi ya da bir doğru üzerindeki noktalar, bu içsel gözlemle anlaşılabilir.
Ancak her iki yaklaşım da ciddi zorluklarla karşı karşıyadır. İlk görüş olan inşacı (constructivist) yaklaşım, matematiksel uygulamaları sınırlayan bir bakış açısıdır. Örneğin, İkiz Asal Sayılar Varsayımı ya doğrudur ya da yanlıştır demek isteriz. Ama eğer bu doğruluk bizim zihinsel üretimimize bağlıysa ve biz bu soruyu çözemiyorsak, o zaman varsayımın doğru ya da yanlış olduğuna karar verecek hiçbir temel kalmaz.
İkinci görüş olan platoncu yaklaşım, bu sorunu yaşamaz. Çünkü sayı dizisinin bağımsız varlığı kabul edildiğinde, İkiz Asal Sayılar Varsayımı ya doğrudur ya da yanlıştır; bunun mutlaka bir cevabı vardır. Ne var ki platoncu yaklaşımın temel sorunu şudur: Bu zihinsel “algı” tam olarak nedir ve nasıl işler? Matematiksel nesneleri nasıl kavrarız ve onlar hakkında nasıl bilgi ediniriz? Bu sorulara hâlâ tatmin edici bir yanıt verilememiştir.
Matematik Hem Keşiftir Hem de İcat
Matematiğin doğasına dair tartışma günümüzde de tüm canlılığıyla sürüyor ve kesin bir yanıt vermek hâlâ mümkün görünmüyor. Ancak yalnızca “matematik keşif midir, icat mı?” sorusuyla yetinmek, meseleyi fazlasıyla sadeleştiriyor. Bu iki uç arasında daha karmaşık bir gerçeklik de olasıdır.
Matematiğin etkisi iki şekilde kendini gösterir: etkin ve edilgin. Bazen bilim insanları, gerçek dünyayı niceliksel olarak tanımlamak için özel matematiksel yöntemler geliştirir. Örneğin Newton, hareketi ve değişimi açıklamak için kalkülüsü formüle etti. Bu tür araçların işe yaraması beklenir; çünkü ihtiyaçtan doğarlar.
Daha da şaşırtıcı olan, matematiğin yalnızca ihtiyaçtan değil, bazen tamamen meraktan doğan alanlarının bile yıllar sonra bilimsel atılımlara temel oluşturmasıdır. Matematikçiler zaman zaman belirli bir uygulama amacı gütmeden, soyut düşüncenin izinden giderek tüm bir alanı geliştirir.
Ve onlarca, hatta yüzlerce yıl sonra, fizikçiler bu soyut yapıların doğa olaylarını açıklamada tam da ihtiyaç duydukları şey olduğunu keşfeder. Bu tür edilgin etkililik örnekleri saymakla bitmez.
Örneğin Fransız matematikçi Évariste Galois, 1800’lerin başında yalnızca polinom denklemlerinin çözülebilirliğini incelemek için grup kuramını geliştirdi. 1960’larda fizikçiler Murray Gell-Mann ve Yuval Ne’eman, SU(3) adı verilen özel bir grubun, hadron adı verilen atom altı parçacıkların davranışlarını yansıttığını gösterdi. Bu bağlantı, modern parçacık fiziğinin temelini oluşturdu.
1960’larda fizikçiler Murray Gell-Mann ve Yuval Ne’eman, SU(3) adı verilen özel bir grubun, hadron adı verilen atom altı parçacıkların davranışlarını yansıttığını gösterdi. Bu bağlantı, modern parçacık fiziğinin temelini oluşturdu.
İngiliz matematikçi G.H. Hardy bir zamanlar şöyle demişti: “Sayı kuramı henüz hiçbir savaş amacı için işe yaramadı.” Ancak sayı kuramı alanındaki keşifleri, yıllar sonra kriptografi gibi uygulamalarda kullanıldı.
Aynı şekilde, Bernhard Riemann’ın 1854’te geliştirdiği Öklid dışı geometriler—örneğin paralel çizgilerin yakınlaştığı veya uzaklaştığı uzaylar—bir asır sonra Einstein tarafından genel görelilik kuramının temelini oluşturdu.
Buradan bir desen çıkıyor. İnsanlar çevresindeki dünyadan şekiller, çizgiler, kümeler, gruplar gibi soyut unsurları alarak matematiksel kavramları icat eder. Ardından bu kavramlar arasındaki ilişkiler keşfedilir.
Sonuç olarak
“Matematik icat mı, keşif mi?” sorusuna verilebilecek en tutarlı yanıt ikisi birden olacaktır. Matematiksel yapıların var olabileceği alanlar keşfedilmeyi beklerken, bu alanların nasıl inşa edileceği bizim seçimlerimize bağlıdır.
Olasılıklar dış dünyada mevcuttur, fakat onları gerçeğe dönüştüren şey insan zihninin yaratıcılığıdır. Bu ikili etkileşim—keşif ve icat—matematiği hem evrensel hem de insana özgü kılan temel dinamiktir.
Kaynaklar ve ileri okumalar:
- How Numbers Work; Discover the strange and beautiful world of mathematics. New Scientist’s Instant Expert books
- Is Mathematics An Invention Or A Discovery? Yayınlanma tarihi: 10 Ocak 2022; Bağlantı:https://www.scienceabc.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel