Bir tarlanın ortasında dururken, yuvarlak bir gezegen üzerinde yaşadığımızı kolayca unutabiliriz. Dünya’ya kıyasla o kadar küçüğüz ki, kendi bakış açımızdan her şey düz görünür. Dünya bu tür biçimlerle doludur. Üzerinde yaşayan bir karınca için düz görünen, ama küresel ölçekte daha karmaşık bir yapıya sahip olan biçimler. Matematikçiler bu tür yapılara manifold adını verir.

Manifoldlar, 19. yüzyılın ortalarında Bernhard Riemann tarafından tanıtıldı ve matematikçilerin uzay kavramına bakışını kökten değiştirdi. Bu yeni perspektif, daha yüksek boyutlu uzayların katı biçimde incelenmesini mümkün kıldı.
Bu gelişme, manifoldları araştırmaya adanmış modern topolojinin doğmasına yol açtı. Zamanla manifoldlar; geometri, dinamik sistemler, veri analizi ve fizik gibi birçok alanda merkezi bir rol üstlenmeye başladı.
Günümüzde manifoldlar, matematikçilere çok çeşitli problemleri çözmede ortak bir dil sunmaktadır. Matematikteki önemleri, alfabenin dil için taşıdığı role benzetilir. Peki, manifoldlar tam olarak nedir ve matematikçilere nasıl bir dil kazandırırlar?
Manifold nedir?
Yüzyıllar boyunca geometri, Öklid uzayındaki nesnelerin incelenmesi anlamına geliyordu. Öklid uzayında her şey beklendiği gibidir: İki nokta arasındaki en kısa yol düz bir çizgidir ve bir üçgenin iç açılarının toplamı 180 derecedir.
Ancak 19. yüzyılın başlarında bazı matematikçiler, farklı türde geometrik uzayları araştırmaya başladı. Bu tür uzaylarda paralel doğrular sonunda kesişebilir, üçgenlerin iç açıları ise 180 dereceden büyük ya da küçük olabilir.
Matematik camiası, bu dönüşümü kabullenmekte zorlandı. Buna rağmen bazı matematikçiler bu fikirleri daha da ileriye taşımayı arzuladı. Bu isimlerden biri, gençliğinde aslında ilahiyat eğitimi almayı planlayan Bernhard Riemann’dı.

Riemann 1854’te de, Göttingen Üniversitesi’nde bir öğretim görevi almak için bir ders vermek zorunda kaldı. Kendisine verilen konu geometrinin temelleriydi. Topluluk önünde konuşma korkusuna rağmen, Gauss’un yüzey geometrisine dair fikirlerini keyfi sayıda boyuta genelleştiren yeni bir kuram anlattı. Anlatılanlar yalnızca matematiği değil, felsefe ve fiziği de kapsıyordu.
Çoğu matematikçi Riemann’ın fikirlerini fazla muğlak bulsa da, Riemann tüm olası geometrileri ve her sayıda boyutu kapsayan bir kavram ortaya koymuştu. Bu kavramın adı manifolddu.
“Manifold” terimi, Riemann’ın Almanca “çeşitlilik” veya “çokluk” anlamına gelen Mannigfaltigkeit sözcüğünden gelir. Bir manifold, her bir noktasına yeterince yakından bakıldığında, tanıdık düz uzay gibi davranan bir yapıdır. Yani küçük ölçekte karmaşık görünmez.
Örneğin, bir çember tek boyutlu bir manifolddur. Çember üzerindeki herhangi bir noktaya yeterince yaklaştığınızda, o bölge düz bir doğru gibi görünür. Çemberin üzerinde yaşayan bir karınca, onun aslında kapalı ve yuvarlak bir şekil olduğunu fark edemez.
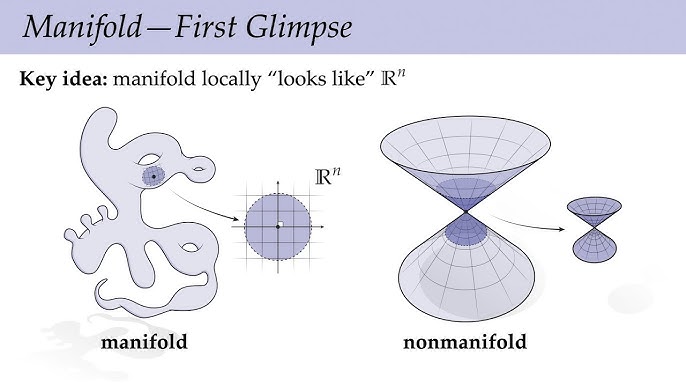
Buna karşılık, sekiz biçimindeki bir eğri bu özelliği taşımaz. Özellikle kendi üzerine kapandığı noktada, ne kadar yaklaşırsanız yaklaşın, yapı düz bir doğruya benzemez. O noktada yaşayan bir karınca, bulunduğu yerin “düz” bir ortam olmadığını hemen fark eder. Bu nedenle sekiz biçimi bir manifold olmaz.
Aynı fikir iki boyut için de geçerlidir. Dünya’nın yüzeyi bir manifolddur; çünkü yeterince yakından bakıldığında, her yerde düz bir zemin gibi görünür. Buna karşılık, çift koni yüzeyi bir manifold değildir.
Manifoldlar Ne İşe Yarar?
Manifoldlar, matematikçilerin temel bir sorununu çözer. Bir ipi masanın üzerine koyup uçlarını kaldırmadan birleştirirseniz basit bir halka elde edersiniz. Aynı ipi havaya kaldırıp uçlarını birleştirirseniz, bu kez ipi kendi üzerinden geçirerek çok sayıda farklı düğüm oluşturabilirsiniz. Oysa her iki durumda da söz konusu nesne aynıdır. Farklı olan, ipin iki boyutlu bir yüzeyde mi yoksa üç boyutlu bir ortamda mı ele alındığıdır.
Matematikçiler bu tür belirsizliklerden kaçınmak için şeklin bulunduğu ortamı değil, yapının kendi iç özelliklerini merkeze alır. Manifold kavramı tam burada devreye girer. Bir manifoldun temel özelliği şudur: Herhangi bir noktasına çok yakından bakıldığında, ortam basit ve düz görünür. Bu sayede karmaşık bir yapıyı, küçük parçalar hâlinde ve tanıdık bir çerçevede incelemek mümkün olur.
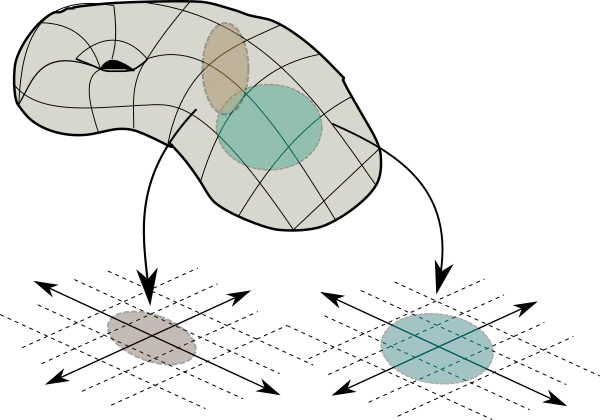
Bunu sistemli biçimde yapmak için matematikçiler, bir manifoldu kısmen üst üste binen küçük parçalara ayırır. Bu parçalardan her biri, üzerinde bulunduğunuz yeri tanımlayan bir koordinat sistemiyle ifade edilir. Bu temsillere “harita” denir. Önemli olan, bu haritaların örtüştüğü bölgelerde koordinatların birbirine nasıl dönüştüğünü de açıkça tanımlamaktır. Tüm bu haritaların oluşturduğu bütün ise “atlas” olarak adlandırılır.
Bu atlas sayesinde, karmaşık bir yapıyı tek seferde anlamaya çalışmak yerine, küçük parçalar üzerinden ilerlemek mümkün olur.
Manifoldlar, evreni anlamamız açısından da kritik bir role sahiptir. Einstein, genel görelilik kuramında uzay-zamanı dört boyutlu bir manifold olarak tanımladı ve yerçekimini bu yapının eğriliğiyle açıkladı. Etrafımızda gördüğümüz üç boyutlu uzay da bir manifolddur.
Manifoldlar ilk bakışta ortada yokmuş gibi göründüğünde bile, matematikçiler ve fizikçiler problemlerini bu dilde yeniden yazmaya çalışır. Bunun nedeni, manifoldların sunduğu kavramsal araçların son derece kullanışlı olmasıdır. Mesela matematikçiler, karmaşık cebirsel denklemlerin çözümlerini de çoğu zaman bir manifold olarak ele alır. Bu sayede çözümlerin yapısını daha iyi kavrarlar.
Sonuç Olarak
Bilim insanlarının manifoldları nasıl kullandığını sormak, sayıları nasıl kullandıklarını sormaya benzer. Çünkü manifoldlar tek bir alana ait değildir. Denklemlerin çözümlerinden veri kümelerinin yapısına kadar pek çok sorunun altında aynı düşünme biçimi yatar. Bu yüzden manifoldlar, modern bilimin sessiz ama kurucu araçlarından biridir.
Kaynaklar ve ileri okumalar
What Is a Manifold?. Kaynak site: Quanta Magazine. Yayınlanma tarihi: 4 Kasım 2025. Bağlantı: What Is a Manifold?
Matematiksel





