Üç Kutu paradoksu Fransız matematikçi Joseph Bertrand’ın (1822–1900) Olasılık Hesabı (Calcul des probabilités) adlı kitabında, olasılık kuramının incelikleriyle henüz tanışmamış kişilerin nasıl kolayca yanıltılabileceğini göstermek için sunduğu görünen paradokslardan biridir
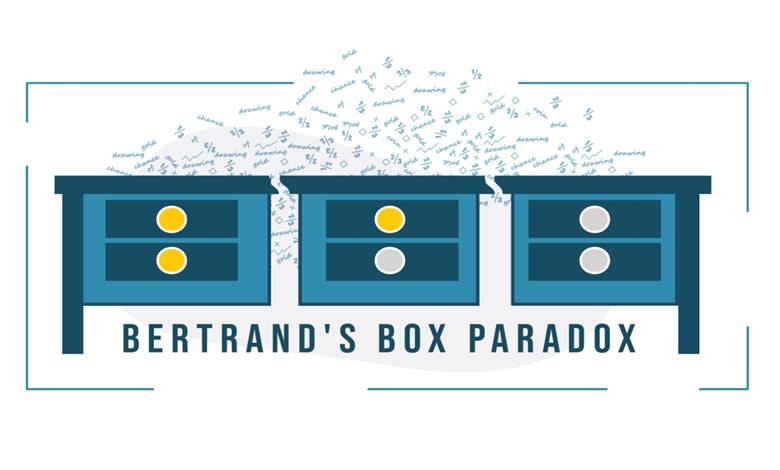
Önünüzde üç kutu var ve her birinin iki çekmecesi bulunuyor. Bir kutunun iki çekmecesinde de birer altın para var. İkinci kutunun iki çekmecesinde de birer gümüş para var. Üçüncü kutuda ise bir çekmecede gümüş, diğerinde altın para bulunuyor. Özetle: altın–altın kutusu, gümüş–gümüş kutusu ve altın–gümüş kutusu var.
Kutulardan birini rastgele seçiyorsunuz, sonra o kutudan bir çekmeceyi rastgele açıyorsunuz. Çekmeceden bir altın para çıkıyor. Aynı kutudaki diğer çekmecenin de altın para içerme olasılığı nedir? Yüzde elli mi?

“Evet” dediyseniz, oldukça kalabalık bir gruptasınız. Bu yanıtı verenler genellikle şöyle düşünür: Madem gümüş para çekmedik, seçtiğimiz kutu iki gümüş paranın bulunduğu kutu olamaz. O hâlde seçtiğimiz kutu ya altın–altın kutusudur ya da altın–gümüş kutusudur.
Bu iki kutudan birini seçmiş olma ihtimalimiz de yarı yarıya olduğuna göre, ikinci çekmecede altın ya da gümüş bulunma olasılığı da yarı yarıya olmalıdır. Kulağa makul geliyor… ama yanlıştır.
Üç Kutu Paradoksunun Çözümü Nedir?
Gümüş–gümüş kutusu elendiğinde, altın para çekilmiş olmasını açıklayan üç olasılık kalır: biri altın–gümüş kutusundaki tek altın para, diğer ikisi altın–altın kutusundaki iki altından biridir. Yani altın gördüğümüzde, bu üç eşit olasılıktan hangisinin gerçekleştiğini bilemeyiz. Ancak ikisi altın–altın kutusuna, biri altın–gümüş kutusuna ait olduğu için, kutunun altın–altın olma ihtimali üçte iki, altın–gümüş olma ihtimali üçte birdir.
1980’lerde psikologlar Maya Bar-Hillel ve Ruma Falk, benzer bir mantıkla bir deney yaptı. Öğrencilere üç kâğıt içeren bir şapka gösterildi: biri çift kırmızı, biri çift beyaz, biri de kırmızı–beyaz. Rastgele çekilen bir kâğıt, yalnızca bir yüzü görünecek şekilde masaya kondu. Soru şuydu: Görünen yüz kırmızıysa, diğer yüzün de kırmızı olma olasılığı nedir?
Yalnızca kırmızı yüz gösteren olasılıklar dikkate alındığında, çift kırmızı kâğıt bunu iki şekilde, kırmızı–beyaz kâğıt ise tek şekilde yapabilir. Yani üç eşit olasılıktan ikisi çift kırmızıdan, biri kırmızı–beyazdan gelir. Dolayısıyla doğru yanıt üçte ikidir. Aynı mantık beyaz yüz için de geçerlidir.
Buna rağmen elli üç öğrencinin otuz beşi soruyu yanlış yanıtladı; yalnızca üç öğrenci doğru cevap olan üçte ikiyi verdi. Araştırmacılar, insanların çoğunun bu tür sorularda yaptığı bu hatayı, elde kalan olasılıkları otomatik olarak eşit sanma eğilimi olarak tanımladı ve buna “sonradan eşit olasılık atfetme yanılgısı” adını verdi.
Bertrand Paradoksu İle İlgili Bir Başka Örnek
Bar-Hillel ile Falk, Bertrand’ın olasılık paradoksuna ait bir başka örneği de şöyle anlatır. Diyelim ki iki çocuk babası olduğu bilinen Bay Smith’i sokakta bir erkek çocukla yürürken görüyorsunuz ve Bay Smith bu çocuğu “oğlum” diye tanıtıyor. Bu durumda, diğer çocuğunun da erkek olma olasılığı nedir? Peki Bay Smith bu çocuğu özellikle “büyük oğlum” diye tanıtırsa, olasılık değişir mi?
İlk durumda, iki çocuk için dört olasılık vardır: erkek–erkek, erkek–kız, kız–erkek ve kız–kız. Yanındaki çocuğun erkek olduğunu bildiğimiz için kız–kız olasılığı elenir. Geriye üç olasılık kalır ve bunlardan yalnızca biri erkek–erkektir. Dolayısıyla, diğer çocuğun da erkek olma olasılığı üçte birdir.
İkinci durumda ise olasılık değişir. Çünkü Bay Smith, yanındaki çocuğun özellikle büyük çocuk olduğunu söylediğinde, artık olasılıkları büyük çocuğu önce yazarak düşünürüz. Bu kez olası durumlar erkek–erkek, erkek–kız, kız–erkek ve kız–kızdır. Büyük çocuğun erkek olduğu söylendiği için kız–kız ve kız–erkek elenir. Geriye yalnızca erkek–erkek ve erkek–kız kalır. Bu durumda küçük çocuğun da erkek olma olasılığı bire iki, yani yüzde ellidir.
Detaylar için: Erkek mi Kız mı? İki Çocuk Paradoksu Nedir?
Sonuç Olarak
Bu örnek, eklenen küçük bir bilginin —örneğin çocuğun yaş sırasının belirtilmesinin— olasılıkları nasıl kökten değiştirebildiğini gösterir. Üç kurt paradoksunda da aslında iki gümüş paranın bulunduğu kutu yanıltıcı bir ayrıntıdır. Bertrand bu kutuyu yalnızca altın ve gümüş paraların toplam sayısını eşitlemek için eklemiştir.
Kaynaklar ve ileri okumalar
- Britannica, The Editors of Encyclopaedia. “Joseph Bertrand”. Encyclopedia Britannica, 17 Apr. 2024, https://www.britannica.com/biography/Joseph-Bertrand. Accessed 5 May 2024..
- The Easiest Problem Everyone Gets Wrong. Kaynak site: Youtube. – Vsauce. Bağlantı: https://www.youtube.com/watch?v=ytfCdqWhmdg
- Saenen L, Heyvaert M, Van Dooren W, Schaeken W, Onghena P. Why Humans Fail in Solving the Monty Hall Dilemma: A Systematic Review. Psychol Belg. 2018 Jun 1;58(1):128-158. doi: 10.5334/pb.274. PMID: 30479812; PMCID: PMC6194549.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel