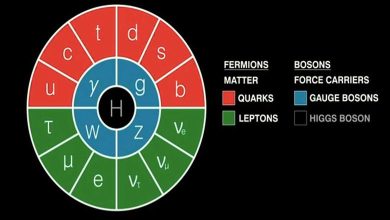
Emmy Noether, temel fizik yasalarının basit simetrilerin bir sonucu olduğunu gösterdi. Bir asır sonra, Noether teoremi fiziği şekillendirmeye devam ediyor.

Doğanın yasalarının evrenselliği, büyüleyici matematiksel kökenlere sahiptir ve bilimin en güçlü fikirlerinden biriyle, yani simetriyle yakından ilişkilidir.
Simetri kavramını herkes bir ölçüde tanır. Bir kareyi ortasından geçen bir dikey çizgiyle ikiye böldüğünüzde ve iki yarıyı yer değiştirirseniz şekil aynı kalır. Aynı durum, kareyi yatay ya da çapraz biçimde bölüp döndürdüğünüzde de geçerlidir. Dairede ise simetri daha da belirgindir; hangi açıyla döndürürseniz döndürün görünümü değişmez.

Fizikte simetri, yalnızca şekillerin dönme ya da yansımada aynı kalması anlamına gelmez; evrenin yapısı hakkında çok daha derin bir şeyi anlatır. Fizikçiler bir sistemin simetrisinden söz ettiğinde, sistemin bazı özelliklerinin belirli değişimlere rağmen sabit kaldığını kastederler. Bu, son derece güçlü bir kavramdır. “Küresel simetri” doğa yasalarının, her yerde aynı biçimde uygulanan bir dönüşümle değişmeden kalmasını ifade eder.
1915’te Emmy Noether, doğada böyle bir simetri gördüğümüz her durumda, buna karşılık gelen bir korunum yasasının bulunacağını keşfetti. Örneğin, fizik yasaları bir yerden diğerine değişmiyorsa momentum korunur; bir andan diğerine değişmiyorsa enerji korunur. Noether teoremi, simetri ve korunum yasalarını birbirine bağlar.

Noether Teoremi Nedir?
Albert Einstein herkese “yaratıcı matematik dehası” demez. Ama Emmy Noether için demişti. Emmy Noether, simetri kavramını enerji ve momentum gibi nicelikleri koruyan temel yasalara bağlayarak evren anlayışımızda devrim yarattı.
1918’de Noether araştırmalarının sonuçlarını iki önemli teoremde yayımladı. Bunlardan biri, küçük uzay bölgelerindeki korunma yasalarını açıklığa kavuşturdu. Bu, daha sonra kuantum alan teorisindeki simetrileri anlamada büyük önem taşıyacaktı. Diğeri ise bugün “Noether teoremi” olarak bilinir ve her korunma yasasının ardında daha derin bir simetri bulunduğunu söyler.
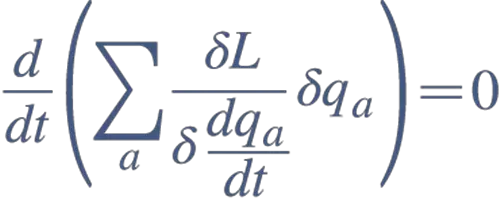
Bir deney yaptığınızı düşünün. Sonra on metre sola gidip aynı deneyi tekrarlıyorsunuz. Sonuçlar değişmez, çünkü fizik yasaları bir yerden başka bir yere gidince değişmez. Buna yer değiştirme simetrisi (translation symmetry) denir.
Şimdi birkaç gün bekleyip deneyi yeniden yapın. Sonuçlar yine aynı çıkar, çünkü fizik yasaları zaman geçse de değişmez. Bu da zaman-yer değiştirme simetrisi (time-translation symmetry) olarak adlandırılır.
Noether bu tür simetrilerden yola çıkarak bunların matematiksel sonuçlarını araştırdı. Çalışmalarında fiziksel sistemleri tanımlamak için kullanılan ortak bir matematiksel araçtan, yani Lagrange fonksiyonundan yararlandı.
İlk bakışta simetriler sistemin fiziğini etkilemiyor gibi görünüyordu, çünkü Lagrange denklemleri bu değişimlerden etkilenmiyordu. Fakat Noether, simetrilerin mutlaka önemli bir matematiksel anlamı olması gerektiğini fark etti; çünkü bu simetriler, sistemin nasıl davranabileceğini sınırlandırıyordu.
Bu sınırlamanın ne anlama geldiğini adım adım çözerek, Lagrange matematiği içinden değişmeyen bir nicelik buldu. İşte bu nicelik, sistemde korunan fiziksel büyüklüğe karşılık geliyordu.
Fizikçi ve matematikçi Feza Gürsey 1983’te şöyle yazmıştı. “Noether teoreminden önce enerji korunumu ilkesi gizemle örtülmüştü… Noether’in yalın ama derin matematiksel formülasyonu fiziğin gizemini büyük ölçüde ortadan kaldırdı.”
Noether Teoremi Fiziği Nasıl Değiştirdi?
Noether’in teoremi kuramsal fizikte son derece yararlı oldu ve derin felsefi sonuçlar doğurdu. Fizikçiler, doğanın dilinin matematik olduğunu doğrular biçimde, gizli ve daha temel simetrileri keşfetmeye çalıştılar. Bu da kuvvetlerin birleştirilmesi yönündeki araştırmaları besledi.
Fizikçiler, simetrilerin verdiği yasaları sınayarak, yani “simetri kırılması” adı verilen olguyu araştırarak da çok şey öğrendiler ve bu uğraş onlara birçok Nobel Ödülü kazandırdı.
Yuvarlak bir masada oturduğunuzu ve ekmek tabağınızın hangi yanda olduğunu unuttuğunuzu varsayın. Kimse sofraya dokunmadan önce düzen kusursuz biçimde simetriktir. Ama biri ekmeğini solundaki tabağa koyduğunda bu simetri bozulur ve diğerleri de aynı düzeni izler.
Simetri kırılması, maddenin en temel parçacıklarını ve aralarındaki kuvvetleri anlamamızda kilit rol oynadı. En çarpıcı örnek, atom çekirdeği içinde etkili olan zayıf nükleer kuvvettir. 1950’lere kadar fizikçiler, evrenin ayna yansımasında da yasaların değişmeden kaldığını düşünüyordu.
Buna “parite korunumu” denir ve doğadaki diğer üç kuvvet—yerçekimi, elektromanyetizma ve güçlü nükleer kuvvet—bu kurala uyar. Ancak zayıf nükleer kuvvet bu simetriyi bozar. Sol ve sağ yer değiştirdiğinde, fizik artık aynı kalmaz. Bu simetri ihlali, bugün parçacık fiziğinin Standart Modeli’nin temel taşlarından biridir.
Sonuç Olarak
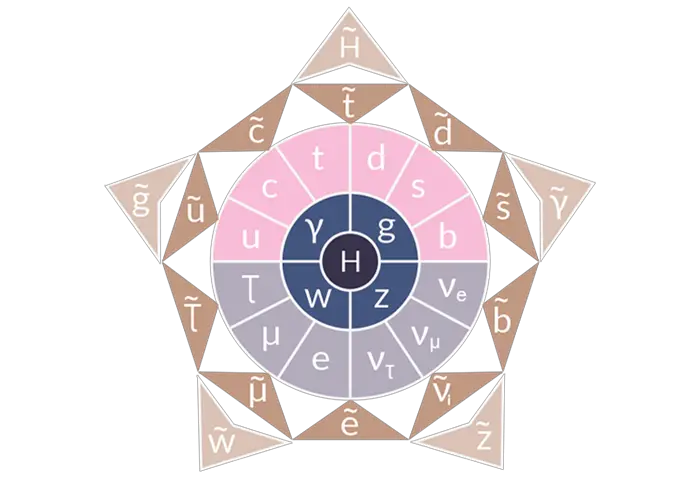
Noether teoreminin gücü, fizikçileri yeni fizik yasalarını keşfetmek için simetrilere yönelmeye teşvik etti. Bu arayışta ortaya çıkan önemli simetrilerden biri “süpersimetri”dir. Anlaması güç bir kavram olsa da, doğruysa karanlık maddenin doğasını ve sicim kuramının kuantum kütleçekimini açıklayıp açıklayamayacağını anlamamıza katkı sağlayabilir.
Ancak süpersimetri, henüz gözlemlenmemiş yeni parçacıklar öngörür. Bu parçacıklar deneysel olarak doğrulanana kadar süpersimetri, yalnızca zarif bir matematiksel kuram olarak kalmaya devam eder. Aradan bir yüzyıldan fazla zaman geçmiş olmasına rağmen, Noether’in sezgileri hâlâ fizikçilerin evreni anlama biçimini derinden etkiliyor.
Kaynaklar ve ileri okumalar:
- In her short life, mathematician Emmy Noether changed the face of physics. Yayınlanma tarihi: 12 Haziran 2018; Bağlantı: https://www.sciencenews.org/
- How Noether’s Theorem Revolutionized Physics Yayınlanma tarihi: 2 Şubat 2025. Kaynak site: Quanta magazine. Bağlantı: How Noether’s Theorem Revolutionized Physics
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel