Kuyrukların nasıl işlediğini anlamak, özellikle tatil dönemlerindeki yoğun alışverişlerde sabırlı kalmayı kolaylaştırır. Temel kuyruk teorisi ilkeleri, hem bireylerin hem işletmelerin bekleme süresini daha verimli yönetmesine yardımcı olur.

Alışverişe çıkmak başta heyecan verse de para ödemek için kasaya ilerlediğinizde süreç genelde bir kabusa dönüşür. Kendinize göre en kısa kuyruğu seçip beklemeye başladığınızda, az evvel hızla ilerleyen kuyruk sanki yavaşlamış gibidir. Bu sırada da yan taraftaki kuyruk daha hızlı ilerlemeye başlar. Peki, zamandan tasarruf etmek adına doğru kuyruğu nasıl seçeceğiz?
Aslında matematikçiler buna bir çözüm üretmek için yıllardır çalışıyor. Sadece bu konuyla ilgilenen bir matematik dalı bile var. Buna kuyruk teorisi denir. Kuyruk teorisi, bir sıranın neden uzun olduğunu açıklayan matematiksel bir bilim alanıdır. Kuyruk, sırasını bekleyen her türlü düzeni tanımlamak için kullanılır.
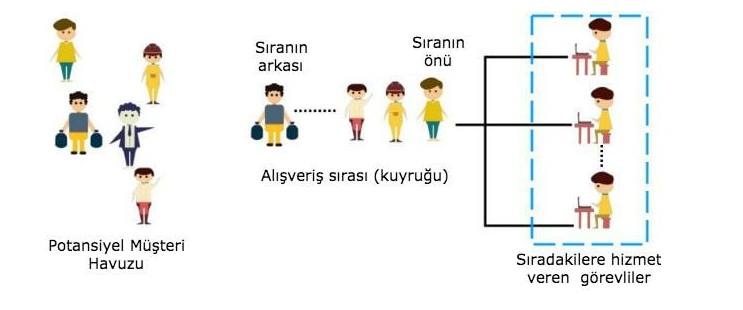
Bir bankada veya bir mağazada sıra beklemek, arama beklemeye alındıktan sonra bir müşteri hizmetleri temsilcisinin aramayı yanıtlamasını beklemek, bir trenin gelmesini beklemek, bir bilgisayarın bir görevi gerçekleştirmesini veya yanıt vermesini beklemek kısacası beklemek ile ilgili her şeyde kuyruk teorisi arka planda bir yerlerde kendine bir yer bulacaktır.
Bir Kuyruk Neden Oluşur?
Bir mağaza yöneticisinin bilerek uzun kuyruklar oluşturması elbette mümkün olsa da, bu kötü bir iş stratejisidir ve pek gerçekçi bir neden sayılmaz.
Daha gerçekçi bir açıklama, yöneticinin maliyeti müşteri memnuniyetinden daha önemli görmesidir. Yani, kasada yeterli personel çalıştırmak yerine tasarrufu tercih eder. Bu yaklaşım kısa vadede masrafı azaltır ama uzun vadede müşteri kaybına yol açar.

Bazı durumlarda uzun kuyruk, hizmete olan yoğun ilgiyi gösterir. İnsanlar yeni bir ürün, konser bileti ya da özel bir fırsat için sıraya giriyorsa, bu kuyruk beklenen değerin bir göstergesidir. Ancak bu, günlük alışverişte nadiren geçerlidir.
En olası neden, sıranın tasarımının yanlış anlaşılmasıdır. Mağaza içinde birkaç kez kıvrılarak ilerleyen bir sıra, gerçekte olduğundan çok daha uzun görünür. Oysa hizmet hızı yüksekse, sıra hızlı ilerler. Görünüşte uzun bir kuyruk, iyi planlanmış bir sistem sayesinde kısa sürede tamamlanabilir.
Kuyruk Teorisinin Arka Planındaki Matematik
Bu sistem tasarımı anlayışı, Little Yasası olarak bilinen bir matematiksel teoreme dayanır. Bu yasa, operasyon araştırmaları alanında uzman MIT profesörü John Dutton Conant Little tarafından geliştirilmiştir.
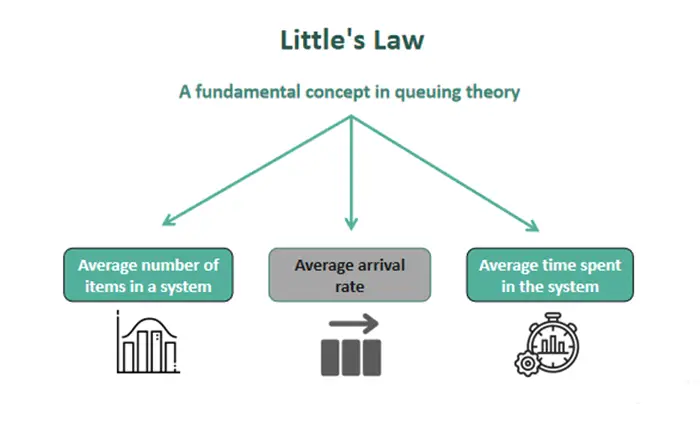
Little Yasası, farklı kuyruk sistemlerinin nasıl çalıştığını incelemek için araştırmacılara matematiksel bir temel sunar. Yasa, belirli bir zaman diliminde sistemdeki ortalama müşteri sayısının, müşterilerin sisteme geliş oranı ile sistemde geçirdikleri ortalama sürenin çarpımına eşit olduğunu söyler.
Bazı sistemlerde hizmet süresi değişkendir; örneğin bir postanede her işlemin süresi farklı olabilir. Bazılarında ise hizmet süresi sabittir; örneğin otomatik bir araç yıkama hattında. Her iki durumda da uygun matematiksel modeller kullanılarak işletmelerin en verimli sistem tasarımı belirlenir.
Little Yasası’nın formülü ve bir kronometre yardımıyla yapılan ölçümler, uzun bir kuyruğun aslında daha verimli olabileceğini gösterir. Bunu bir örnekle açıklayabiliriz.
Birden fazla kısa kuyruğun bulunduğu bir market düşünelim. Her kasiyer yalnızca kendi sırasındaki müşterilere hizmet verir. Bu model, “tek sunuculu sistem” olarak adlandırılır. Burada hızlı çıkış yapabilmek tamamen doğru sırayı seçmeye bağlıdır. Fakat çoğu kişi bu tahminde yanılır.
Buna karşılık, tek ama uzun bir kuyruğun bulunduğu ve birden fazla kasiyerin sırayla müşterilere hizmet verdiği sistem, genellikle daha hızlıdır. Bankalar, havaalanı güvenlik noktaları veya nüfus müdürlükleri buna örnektir.
Bunun temel nedeni, bir kasiyerin işlemi yavaşlatan bir durumla karşılaşması halinde bu gecikmenin yalnızca kendi işlem süresini etkilemesidir. Diğer çalışanlar sıradaki müşterileri hizmete almaya devam eder. Böylece tek bir gecikme tüm sistemi durdurmaz; zaman kaybı sistemin geneline dengeli biçimde yayılır. Bu nedenle çok kasiyerli tek kuyruk sistemi, pratikte hem adil hem de daha etkilidir.
En Hızlı Kuyruğu Nasıl Seçeriz?
Kuyruklar söz konusu olduğunda sezgisel seçim çoğu zaman en hızlı seçenek değildir. Kuyruğa katıldığınız anda ilerlemenin yavaşladığını hissetmeniz boşuna değildir. Peki gerçekten hangi sıraya girmek daha akıllıcadır? Matematikçiler bu sorular üzerine yıllardır çalışıyor ve bulguları, bekleme süresini azaltmanın düşündüğümüzden daha karmaşık olduğunu gösteriyor.
Genellikle insanlar kısa kuyruğu seçmeyi mantıklı bulur. Kısa sıra, hızlı bir kasiyer ya da az zaman alan müşteriler anlamına geliyor gibi görünür. Ancak bu varsayım çoğu durumda yanlıştır.
Örneğin markette kısa sırada iki dolu alışveriş arabası, uzun sırada ise dört yarı dolu sepet varsa, uzun sırayı seçmek daha mantıklıdır. Kasiyerlerin hızları eşitse belirleyici olan müşteri sayısı değil, kuyruktaki toplam ürün miktarıdır. Fakat arabalar az dolu, sepetler tıka basa doluysa bu farkı gözle anlamak kolay değildir ve doğru tercih yapmak zorlaşır.
Bu örnek, “hizmet süresi dağılımı” kavramını açıklar. Bu dağılım, bir müşteriye hizmet verilmesinin ne kadar süreceğini belirleyen rastgele bir değişkendir. Ortalama hizmet süresini ve bu ortalamadan sapma miktarını içerir. Sapma değeri, müşterilerin farklı hızlarda hizmet alması nedeniyle sürenin nasıl değiştiğini gösterir.

Bir diğer önemli değişken ise “varış oranı”dır. Bu oran, iki müşteri arasında geçen ortalama zamanı ifade eder. Belirli bir anda hizmet almak isteyen kişi sayısı arttığında kuyruklar uzar. Dolayısıyla kuyruk uzunluğunu belirleyen sadece kasiyerin hızı değil, aynı zamanda müşterilerin geliş sıklığıdır.
Feller Paradoksu Nasıl Çalışır?
Bir kuyrukta beklerken çoğu kişi doğru seçimi yapıp yapmadığını merak eder. Örneğin, hizmet veren kişi diğerlerinden daha hızlı mı? Kuyruğun uzunluğunu gözlemlemek kolaydır ve ortalama değerle karşılaştırmak mümkündür.
Bu durum, hizmet süresinin ortalaması ve standart sapmasıyla doğrudan ilişkilidir ve 1930’da geliştirilen Pollaczek–Khinchine formülüyle açıklanır. Bu formül, müşterilerin kuyrukta geliş aralıklarının ortalamasını da dikkate alır.
Ne var ki, sıradaki ilk kişinin hizmet süresini ölçmeye çalışmak genellikle yanıltıcı olur. Çoğu zaman yanlış sırayı seçtiğinizi düşünmenize neden olur. Bu durum Feller paradoksu ya da “gözlem paradoksu” olarak bilinir.
Gerçekte bir mantık hatası değildir, ancak sezgilerimizle çelişir. Kuyruğa katıldığınız anda ölçüm yapmaya başlarsanız, ilk gözlemlediğiniz müşterinin hizmet süresi büyük olasılıkla ortalamadan uzun olur. Bu da sıranın normalden yavaş ilerlediği izlenimini yaratır.
Paradoksun işleyişini bir örnekle açıklamak mümkündür. Diyelim ki bir banka iki tür hizmet sunuyor. İlk hizmet ya sıfır ya da beş dakika sürüyor. İkinci hizmet ise ya on ya da yirmi dakika sürüyor. Her iki seçeneğin de olasılığı eşit. Buna göre bankadaki ortalama hizmet süresi 8,75 dakikadır.
Ancak siz kuyruğa, bir müşterinin hizmet aldığı sırada katılırsanız, o kişinin sıfır dakikalık hizmeti seçme olasılığı ortadan kalkar. Yani o kişi beş, on ya da yirmi dakikalık bir işlem yaptırıyor olmalıdır. Bu durumda ortalama hizmet süresi 11 dakikayı aşar. Üstelik her üç durumda ikisinde, o müşteri on ya da yirmi dakikalık işlemi seçmiştir. Bu yüzden kuyruk olduğundan daha yavaş görünür.
Araştırmalar, insanların çoğunun (sağ ellerini kullanmaları nedeniyle) sağdaki kuyruğu seçme eğilimi gösterdiklerini ortaya koymuştur. Yani çok sayıda paralel kuyruk varsa soldaki kuyruğu seçmek aynı zamanda en kısa kuyruğu seçmek anlamına gelir.
Sonuç olarak;
En hızlı kuyruğu bulmak için matematikten yararlanmak mümkündür, ancak doğru verilere sahip olunmadığında bu çaba pek işe yaramaz. Dahası, zihinsel rahatlık açısından da en iyi yöntem çoğu zaman bir sırayı seçip kararın arkasına bakmamaktır. Başka seçeneklere takılmadan beklemek, hem zamanı daha katlanılabilir kılar hem de yanlış sırada olduğunuz hissini azaltır.
Kaynaklar ve ileri okumalar:
- There’s a mathematical formula for choosing the fastest queue. Yayınlanma tarihi: 7 Mayıs 2017; Kaynak site: Conversation. Bağlantı: There’s a mathematical formula for choosing the fastest queue/
- Shunko, Masha & Niederhoff, Julie & Rosokha, Yaroslav. (2016). Humans Are Not Machines: The Behavioral Impact of Queueing Design on Service Time. SSRN Electronic Journal. 10.2139/ssrn.2479342.
- Lim, Grace & Lim, Annamarie & Quinn, Beth & Carvalho, Brendan & Zakowski, Mark & Lynde, Grant. (2023). Obstetric operating room staffing and operating efficiency using queueing theory. BMC health services research. 23. 1147. 10.1186/s12913-023-10143-0.
Matematiksel





