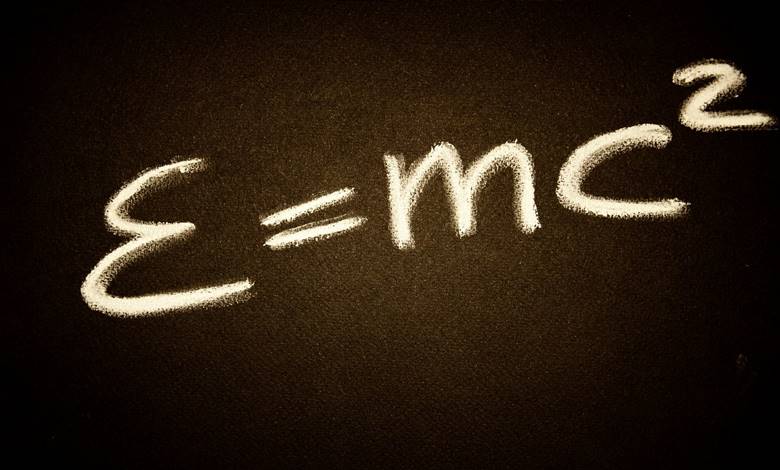
E=mc² denklemi, evrenin dokusuna işlemiş gizli bir birliği açıklayan, dünyanın en ünlü denklemidir. Bu formül bize enerji, ışık ve madde arasındaki bağı anlatır. Bu nedenle Kütle-Enerji eşitliği olarak da bilinmektedir.
Bu denklem 1946 Time dergisinin kapağında, bir mercan resifinin üzerinde yükselen mantar bulutunun üzerine yazılmıştır. Çünkü E=mc² denklemi aynı zamanda atom bombasının ardındaki denklemdir.

1905’te başlayan bir dizi makaleyle Einstein’ın özel görelilik kuramı, uzay ve zaman kavramlarını tek bir varlıkta, yani uzay-zamanda birleştirerek devrim yarattı. Ancak, özel göreliliğin en ünlü unsuru ilk makalede yoktu.
E=mc2 ile temsil edilen kütle-enerji denklemi 1905’te yayınlanan daha sonraki bir makalede tanıtılacaktı. Ve tıpkı Einstein’ın uzay ve zamanı zaten birleştirdiği gibi, bu makale de enerji ve kütleyi birleştirecekti.
Yüzlerce yıl itirazsız kabul edilen bir fizik yasası vardı. Bu yasa kütlenin korunması ile ilgiliydi. Ne eklerseniz ekleyin, hangi reaksiyona sokarsanız sokun fark etmez. Başlangıç ve bitiş kütlesi her durumda birbirine eşit olacaktır.
Ancak özel görelilik yasalarına göre kütle, korunan nihai nicelik olamaz. Einstein’ın bir cismin hızının ışık hızına yaklaştıkça kütlesinin artması ile ilgili fikri, modern fiziğin merkezine oturan bu basit ancak dahiyane formülün ortaya çıkmasını sağladı.
Kütle Enerji Denklemi Nedir?
Yazının devamını okumaya zamanı olmayacaklar ve sadece bu denklemin ne olduğunu öğrenmek isteyenler için öncelikle kısa bilgi verelim. Esasen bu denklem bize kütle ve enerjinin aynı şeyin farklı biçimleri olduğunu söyler. Yani kütle bir enerji biçimidir. Muhtemelen bilmeniz gereken ikinci en önemli bilgi, Evrenin bu iki yönünün birbirinin yerine geçebileceği ve hafifletici faktörün ışık hızının karesi olduğu gerçeğidir.
Kütle enerji denklemi ile ilgili belki de en şaşırtıcı şey, aldatıcı bir şekilde basit olmasıdır. Özellikle bunu, yıldızların nasıl enerji saldığını ve böylece tüm yaşamı mümkün kıldığını açıklayan denklem olarak düşünürsek matematiksel hesaplamaların basitliğinden etkilenebiliriz. E = mc2 denklemi fiziğin gücünün ve basitliğinin bir zaferidir.

Hala bizimleyseniz detaylara geçmeden önce bir örnek verelim. Örneğimiz Kaliforniya’daki SLAC Ulusal Laboratuvarı’ndaki doğrusal parçacık hızlandırıcı ile ilgili olacak. Burada güçlü elektromanyetik kuvvetler kullanarak elektronları alır ve onları ışık hızına yakın bir hıza sahip olacak biçimde hızlandırırız.
Elektronlar hızlandırıcının diğer ucunda ortaya çıktıklarında, göreli kütlelerinin şaşırtıcı bir şekilde 40.000 kat arttığını görürüz. Elektronlar yavaşladıkça da bu kütleyi tekrar kaybederler. Böylece, kütlesini artıran şeyin kinetik enerji olduğunu görebiliriz. Bu bize enerji ve kütlenin birbirine bağlı olduğuna dair iyi bir ipucu verir.
Ancak bu sonuç bizi ilginç bir soruya götürecektir. Hareket enerjisi, hareket halindeki bir nesnenin kütlesi ile ilişkiliyse, nesnenin durgun durumdaki kütlesi ile ilişkili bir enerji var mıdır? Varsa bu ne tür bir enerji olacaktır?
Ortada Gizli Bir Enerji mi Var?
Mekanik enerji, kimyasal enerji, elektrik enerjisi ve kinetik enerji dahil her tür enerjiyi öğrendiniz. Bunların tümü, hareket eden veya tepki veren nesnelerin doğasında bulunan enerjilerdir. Bu enerji biçimleri, bir motoru çalıştırmak, bir ampulü yakmak gibi işler için kullanılmaktadır.
Ancak hareketsiz kütlelerin de kendine özgü enerjisi vardır. Hem de bu muazzam miktarda bir enerjidir. Örneğin bir ceviz tanesi bile içinde bir şehri aydınlatacak kadar enerji taşır. Elbette ki ceviz tanesindeki enerjiyi değil de uranyum atomlarındaki bu enerjiyi serbest bırakırsak sonuçlar yıkıcı olur.
Bunun sonucunda da uranyum atomlarının gluon enerjisi şehirlere elektrik sağlamak ya da onları bombalamak için kullanılabilir. E = mc2 denklemi bize kütleyi dönüştürerek tam olarak ne kadar enerji elde ettiğinizi söyler. Enerjiye dönüştürdüğünüz her 1 kilogram kütle için, 21 Megaton TNT’ye eşdeğer olan 9 × 1016 joule enerji elde edersiniz.
Bu noktada tahmin etmiş olabileceğiniz gibi, enerji ve kütle yakından ilişkili olduğundan ve enerjinin birçok formu olduğundan, bir nesneye kütle artışı vermenin de birçok yolu vardır. Örneğin, bir metal çubuğu ısıtmak, çubuğun kütlesini arttırır. Ancak bu artış esasında o kadar küçük bir miktardır ki fark edemezsiniz.
E=mc² Denklemi Genel Görelilik Kapısını Aralamıştı
Özel göreliliğin ortaya çıkışına fiziği temelde iki yasa yönetiyordu: kütlenin korunumu ve enerjinin korunumu. Özel görelilik, bunun yerine korunan şeyin kütle veya enerji değil, sistemin toplam göreli enerjisi olduğunu öne sürerek buna meydan okudu. Kütle ve enerjinin denk olduğu gerçeği ise Einstein’ı zirveye taşıdı.
Şimdi bir madde ve bir antimadde parçacığına sahip olduğunuzu hayal edin. Onları yok edebilirsiniz. Ve E = mc2 ile uyumlu sayıda fotonlar elde edersiniz. Şimdi, bu parçacık / antiparçacık çiftinin sanki uzaydan düşmüşler gibi hızla hareket ettiğini düşünün. Sonra Dünya yüzeyine yakın bir yerde yok olsunlar. Bu fotonlar artık ekstra bir enerjiye daha sahip olacaklardır. Bu ek enerji de düşerek kazandıkları kinetik enerjiden gelecektir.
Kütle Enerji Denkleminde Neden Işık Hızının Karesi Alınıyor?
Bildiğiniz gibi denklemde c harfi evrensel bir sabit olan ışık hızını temsil eder. Dolayısıyla aslında denklem “Enerji, maddenin kütlesinin ışık hızının karesiyle çarpımına eşittir.” biçimindedir. Peki, enerji üretmek için neden maddeyi ışık hızıyla çarpmanız gerekiyor?
Bunun nedeni, ister ışık dalgaları ister radyasyon olsun, enerjinin ışık hızında hareket etmesidir. Bu, saniyede 300.000 kilometre’dir. Bir nükleer santralde veya atom bombasında bir atomu parçaladığımızda ortaya çıkan enerji ışık hızında açığa çıkar. Ama neden ışık hızının karesi alınır?
Bunun nedeni, kinetik enerjinin kütle ile orantılı olmasıdır. Kinetik enerji formülü aşağıda gördüğünüz gibidir. Bir nesneyi hızlandırdığınızda, kinetik enerji hızın karesi ile orantılı artar.
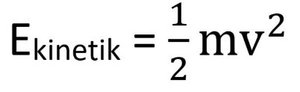
Işık hızının karesi muazzam bir sayıdır ve çok küçük miktarlardaki maddede bile ne kadar enerji olduğunu gösterir. Bunun yaygın bir örneği, 1 gram suyun — tüm kütlesi E=mc² yoluyla saf enerjiye dönüştürülürse — patlayan 20.000 ton (18.143 metrik ton) TNT kadar enerji içermesidir. Az miktarda uranyum veya plütonyumun büyük bir atomik patlama üretmesinin nedeni budur.
Einstein’ın denklemi, nükleer enerji ve nükleer tıptan güneşin iç işleyişine kadar çok sayıda teknolojik ilerlemeye kapı açtı. Madde ve enerjinin bir olduğunu bize gösterdi. İkinci Dünya Savaşı’nın sonunda Hiroşima ve Nagazaki’yi harap eden nükleer silahlar da enerji kütle denkleminin bir sonucudur.
Yaşamı boyunca bir pasifist olan Einstein’ın adının sonsuza dek insan doğasının en yıkıcı unsurlarının nihai düzenlemesiyle bağlantılı olması talihsiz bir durumdur. Göz atmak isterseniz: Bilim İnsanlarının Seçtiği En Güzel 10 Denklem
Kaynaklar ve ileri okumalar:
- The Three Meanings Of E=mc^2, Einstein’s Most Famous Equation. Yayınlanma tarihi: 23 Ocak 2018; Bağlantı: https://www.forbes.com/
- What does Einstein’s famous equation really mean? Yayınlanma tarihi: 7 Nisan 2021; Bağlantı: https://science.howstuffworks.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel