Matematik tarihindeki en dramatik ve dokunaklı hikâyelerden biri, kuşkusuz Évariste Galois’ya aittir. Bugün adı Galois Teorisi ile anımsanmaktadır.
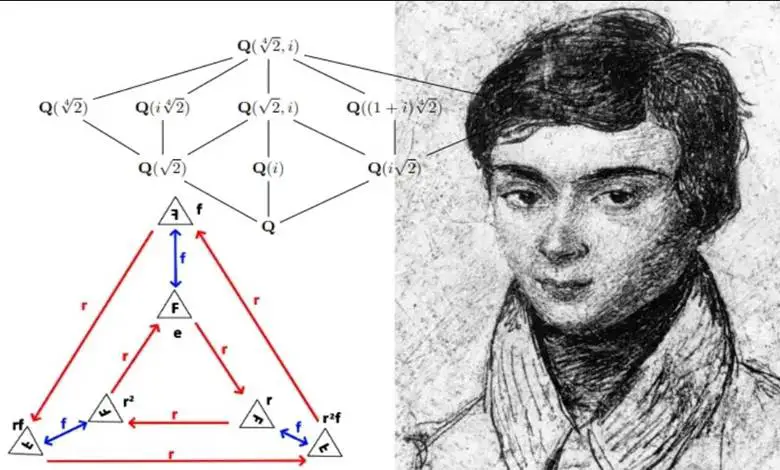
Évariste Galois, 20 yaşında bir düelloda ölümcül şekilde yaralanmadan önce, polinom denklemlerinin gizli yapısını keşfetti. Çözümlerin kendilerini değil, çözümler arasındaki ilişkileri inceleyerek, matematiğin pek çok dalında temel hâline gelen yeni kavramlar geliştirdi.
Kimse Galois’nın 30 Mayıs 1832 sabahının erken saatlerinde neden Paris’te bir düello alanında olduğunu kesin olarak bilmiyor. Ancak rivayete göre, o gecenin büyük bölümünü son el yazmalarını tamamlayarak geçirdi.
Galois’nın çalışmaları, matematikte yaşanan bir çıkmazdan doğdu. 1500’lü yıllarda matematikçiler, x² – 2 ya da x⁴ – 10x² + 22 gibi polinomları inceliyordu. Amaçları, bu denklemlerin köklerini, yani denklemi sıfıra eşitleyen x değerlerini, hesaplamaya yarayan basit formüller bulmaktı. Ancak bu formüller, yalnızca en yüksek derecesi 4’ten küçük ya da 4’e eşit olan polinomlar için bulunabiliyordu.
Galois, bunun ötesine geçerek böyle formüllerin aslında var olmadığını kanıtladı. Kökleri incelemenin yeni bir yolunu geliştirdi. Kökleri tek tek hesaplamak yerine, onların arasındaki cebirsel ilişkileri incelemenin daha anlamlı olduğunu fark etti. Böylece görünüşlerinden çok, aralarındaki karmaşık bağlara odaklandı.
Galois’nın bakış açısı, bir şeklin simetrilerini incelemeye benziyordu. Simetri, bir şekli farklı biçimlerde yeniden konumlandırıp yine aynı görünmesini sağlamaktır. Bir polinomun kökleri arasındaki simetriler de benzer bir fikre dayanır: Köklerin yerlerini değiştirirken aralarındaki cebirsel ilişki korunur.
Galois Teorisi Nedir?
Bazı şekillerin diğerlerinden daha fazla simetrisi vardır. Aynı biçimde bazı polinomların kökleri de diğerlerine göre daha serbest biçimde yer değiştirilebilir. Bu fikir, Galois’nın cebirsel yapıları anlamasında temel bir rol oynadı.
Köklerin birbirleriyle yer değiştirebilmesi ama bu sırada cebirsel yapının bozulmaması, polinomların görünüşte fark edilmeyen özelliklerini anlamada matematikçilere çok şey anlatır. Bunu örneklerle görmek en kolay yoldur. Üç kökü olan iki polinom ele alalım.
f(x) = x³ – 7x + 5
g(x) = x³ – 7x + 7
Kâğıt üzerinde bu iki denklem neredeyse aynı görünür. Ancak perde arkasında, birinin kökleri diğerine göre daha fazla şekilde yer değiştirilebilir. Şimdi f(x)’e bakalım.
Bu polinomun kökleri a, b, c ise, polinomu şu şekilde yazabiliriz: (x – a)(x – b)(x – c) = 0. Bu ifadeyi açarsak x³ – (a + b + c)x² + (ab + ac + bc)x – abc = 0 elde ederiz. Burada x’li terimin katsayısı –7 olduğuna göre, ab + ac + bc = –7 olur.
Köklerin yerlerini değiştirirsek, bu değişiklik, kökler arasındaki cebirsel ilişkiyi bozmaz. Çünkü toplama ve çarpma işlemleri değişme özelliğine sahiptir. Bu durumda, köklerin altı farklı sıralanışı da aynı sonucu verir.
- a, b, c: ab + ac + bc = –7
- b, a, c: ba + bc + ac = –7
- c, b, a: cb + ca + ba = –7
- a, c, b: ac + ab + cb = –7
- b, c, a: bc + ba + ca = –7
- c, a, b: ca + cb + ab = –7
Şimdi ikinci polinoma bakalım. Bu polinomun kökleri r, s ve t olsun. Aynı mantıkla rs + rt + st = –7 bulunur. Ancak g(x) için durum biraz farklıdır: Köklerin hepsi aynı simetriye sahip değildir. Bunun nedeni, kökler arasındaki cebirsel ilişkinin daha karmaşık olmasıdır.
Bu polinomda kökleri birbirine bağlayan ek bir özel ilişki vardır: (r – t)(r – s)(t – s) = 7 (r < s < t varsayımıyla). Bu nedenle, altı farklı sıralamanın sadece üçü, hem rs + rt + st = –7 hem de (r – t)(r – s)(t – s) = 7 denklemlerini aynı anda korur. Galois’nin fark ettiği işte bu tür simetri farklarıydı.
Galois Teorisi İle İlgili Bazı Örnekler
Galois, düşüncelerini “Galois grupları” adını verdiğimiz yeni bir kavramla somutlaştırdı. Bu gruplar, bir polinomun kökleri arasındaki cebirsel ilişkilerin karmaşıklığını tanımlar. Bu ilişkiler içinde kökler farklı biçimlerde yer değiştirebilir; hatta bu değişiklikler geri alınarak kökler başlangıçtaki konumlarına döndürülebilir.
Bu fikir, matematikteki “grup” kavramının özünü oluşturur. Grup, bir şeklin ya da bir polinomun köklerinin sahip olabileceği tüm simetrilerin bir araya geldiği yapıdır. Galois grupları, bu kavramın ilk örneklerindendi. Galois’nin fikirleri zamanla gelişerek bugün “grup teorisi” adını verdiğimiz güçlü ve yaygın bir araştırma alanının temelini oluşturdu.
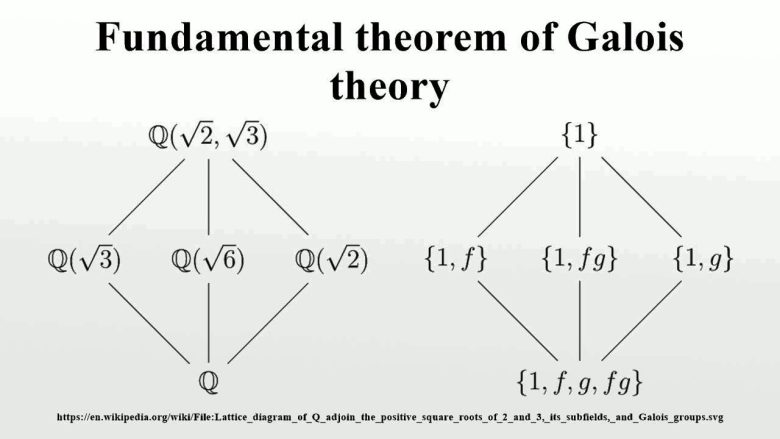
Galois grupları, polinom denklemlerini incelemek için güçlü bir bakış açısı sunar. Bir polinomun Galois grubunu biliyorsan, köklerinin davranışını grup teorisinin araçlarını kullanarak anlayabilirsiniz. Bu yaklaşım, polinom üzerinde doğrudan cebirsel işlemler yaparak elde edilebilecek bilgiden çok daha derin ve aydınlatıcı sonuçlar verir.
Galois grupları, cebir ve sayı teorisindeki pek çok matematiksel yapıyı incelemek için de kullanılır. Bu yöntem, başka yollarla ulaşılamayacak problemlere yeni çözümler sunar. Bu geniş kapsamlı yapı, Galois gruplarının son yüzyılın en önemli matematiksel çalışmalarında merkezi bir rol oynamasını sağladı. Galois grupları, 1994’te Andrew Wiles’ın Fermat’nın Son Teoremi kanıtında da yer aldı.
İkinci, üçüncü ve dördüncü dereceden denklemler için Galois grupları her zaman çözülebilir niteliktedir. Ancak Galois, beşinci dereceden (ya da daha üst dereceden) tipik bir denklemin simetri gruplarının çözümsüz olduğunu göstermiştir. Yani temelinde matematikçilerin onlarca yıllık çabası nafiledir.
Sonuç Olarak
Évariste Galois’nın yaşamı kısa sürdü, ancak en büyük başarısı matematiği yüzyıllar boyunca etkilemeye devam edecek. Bunun nasıl olacağını tam olarak öngörmek zor olsa da, etkisinin kalıcı olacağı kesin.
Kaynaklar ve ileri okumalar
- Galois Groups and the Symmetries of Polynomials. Kaynak site: Quanta Magazine. Yayınlanma tarihi: Bağlantı: Galois Groups and the Symmetries of Polynomials
Matematiksel