Babil matematiği özünde uygulamalı bir matematikti. Amaç matematiği günlük hayattaki problemlere bir çözüm için kullanmaktı.

Dicle ve Fırat nehirleri arasında, birçok büyük antik uygarlığa ev sahipliği yapmış verimli bir toprak uzanır. Bu nehirler günümüz Türkiye’sinden doğar, Irak, Suriye ve İran’dan geçerek Basra Körfezi’ne dökülür. Birlikte, bir zamanlar Mezopotamya olarak bilinen bölgenin doğal sınırlarını oluştururlar.
MÖ 3000’lere gelindiğinde Sümer uygarlığı burada gelişmişti. Sümerler, geniş sulama sistemlerine sahip karmaşık şehirler kurdular. En eski hukuk sistemlerinden birini oluşturdular. Kayıtlar için yazıya ihtiyaç duyduklarından, bilinen en eski yazı sistemi olan çivi yazısını geliştirdiler. Aynı zamanda bir sayı sistemi kurdular.
Sonraki bin yıl içinde Akkadlılar bölgenin hâkim gücü haline geldi. İmparatorlukları çöktüğünde geride iki ayrı Akkadca konuşan topluluk kaldı: kuzeyde Asurlular, güneyde Babilliler. Her biri kendi başına büyük uygarlıklar kurdu, fakat matematik asıl güneyde, Babil’de hız kazandı.

Babil kenti, günümüzdeki Bağdat’ın yaklaşık 100 kilometre güneyinde yer alıyordu ve Babil İmparatorluğu’nun başkentiydi. Yaklaşık MÖ 1792–1750 yılları arasında hüküm süren Kral Hammurabi döneminde Babil büyük bir güç haline geldi. Birçok şehir devletini kontrol altına aldı ve bölgeyi son derece zenginleştirdi. Bu zenginlik ve istikrar, matematikle ilgilenen bir topluluğun gelişmesi ve ilerlemesi için gerekli ortamı sağladı.
Babilliler matematiği birçok pratik amaç için kullandı. Arazi bölüşmek, vergileri hesaplamak, gelir ve bütçe kaydı tutmak gibi işler onların sayı sistemini öğrenmesini sağladı. Cebirle ilgilendiler, üçgenlerle ilgili ve sonradan Pisagor’un adıyla anılacak olan ünlü teoremi keşfettiler. Ayrıca iki sayısının karekökünü altı ondalık basamağa kadar doğru hesapladılar..

Babil Sayı Sistemi
Kullandıkları sayı sistemi Sümerlerden geliyordu ve altmış tabanlıydı. Yani matematiği 60 sayısı üzerine kurmuşlardı. Bugün daireleri 360 dereceye ayırmamızın ve saatleri 60 dakikaya bölmemizin kökeni bu sisteme dayanır.
İlk bakışta 60 tabanlı sistem, karmaşık görünecektir. Fakat 60, “üstün bileşik sayı” olarak adlandırılır; yani birçok böleni vardır. 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ve 60’a tam olarak bölünür. Bu nedenle onluk sistemde zor ya da tekrarlı çıkan birçok kesir, 60 tabanında çok daha düzgün bir şekilde ifade edilir.

Bu da Babillilerin kesirlerle çalışırken büyük kolaylık sağlamasına neden oldu. Yukarıda onların 1’den 59’a kadar olan sayıları göstermek için kullandıkları çivi yazısı semboller yer alır.
Aşağıdaki görsel, MÖ 1800–1600 yıllarına tarihlenen bir Babil kil tabletine aittir. Perspektif vermek gerekirse, bu tarih okulda öğrendiğimiz Yunan matematikçilerinden yaklaşık 1000 yıl öncesine denk gelir.

Arkeologlar, bu tabletin bir karenin köşegeninin hesabını gösterdiğini ortaya çıkardı. Bir kenarı 1 olan karenin köşegeni √2’ye eşittir. Tabletteki işaretlenmiş sayılar, √2’yi yaklaşık olarak hesaplamak için kullanılan katsayılara karşılık gelir.
Bu değerleri modern ondalık sisteme çevirdiğimizde ortaya çıkan sonuç şudur: √2 = 1 + 24/60 + 51/60² + 10/60³ = 1,41421…Babillilerin yaptığı bu hesaplama, bugün kullandığımız değere olağanüstü derecede yakındır. Peki tüm bunları nasıl başardılar?
Babil Matematiğinde Çarpma İşlemi
Cevap onların elindeki kil tabletlerde saklıydı. Şimdi kendinizi Babilli bir öğrenci olarak düşünün. Öğretmeniniz senden 23 × 57 işleminin sonucunu bulmanı istedi. Bunun için önce 23 sayısının katlarını içeren bir tablete bakmanız gerekiyordu. İşte o tablet muhtemelen şöyle görünüyordu. (Tablodaki ondalık sayıların nedeni, bu çarpım tablosunun 60 tabanlı olmasıdır.)
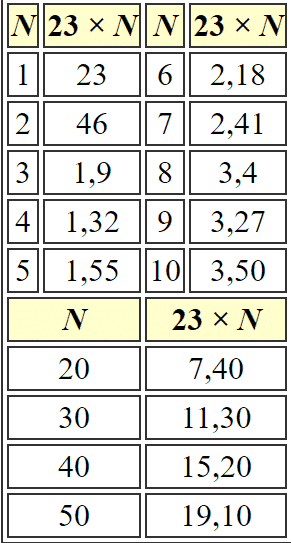
Şimdi 23 × 57 işlemini yapmak için önce 57 sayısını 50 + 7 biçiminde ayırıyoruz ve çarpmanın toplama üzerindeki dağılma özelliğini kullanıyoruz: 23 × 57 = 23 × (50 + 7) = 23 × 50 + 23 × 7
Burada katlar tablosuna baktığımızda 23 × 50 = (19,10)₆₀ ve 23 × 7 = (2,41)₆₀ sonucunu buluyoruz. Bu iki sonucu topladığımızda (21,51)₆₀ elde ederiz. Kısacası Babilliler çarpmayı, toplama yardımıyla yapıyordu. Fakat bunun için birçok farklı tableti kullanmak gerekiyordu. İşte bu yüzden onlar ikinci bir yöntem daha geliştirdiler.
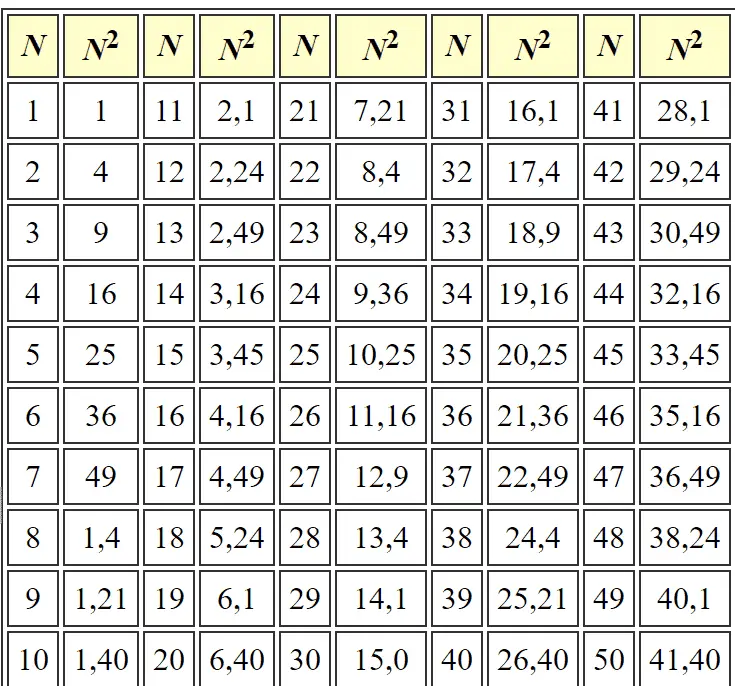
Yukarıdaki tablo 60 tabanında 1’den 50’ye kadar sayıların karelerini göstermektedir. Bu ikinci çarpma yönteminde sayıların karelerinden faydalanmamız gerekiyor. Bunun için de iki özdeşliği bilmeliyiz. Şimdi 26 × 14 işleminin sonucunu iki biçim de bulmaya çalışalım.
| x×y = [(x + y)2 − x2 − y2] ÷ 2 | x×y = [(x + y)2 − (x − y)2] ÷ 4 |
| 26×14 = [(26 + 14)2 – 262 – 142] ÷ 2 | 26 × 14 = [(26 + 14) 2 – (26 – 14) 2] ÷ 4 |
| = [402 – 262 – 142] ÷ 2 | = [402 – 122] ÷ 4 |
| = [(26,40)60 – (11,16)60 – (3,16)60] ÷ 2 | = [(26,40) 60 – (2,24) 60] ÷ 4 |
| = (12,8)60 ÷ 2 = (6,4)60 . | = (24,16) 60 ÷ 4 = (6,4) 60. |
Babil karekök algoritması
Buraya kadar anlattıklarımız tarihsel açıdan değerli olsa da günlük hayatta işimizi kolaylaştıracak pratik faydaları sınırlı. Fakat konu Babillilerin kullandığı karekök bulma yöntemine geldiğinde durum değişiyor. Bu yöntemden gerçekten bazı pratik ipuçları çıkarabilirsiniz.
Bugün Hero’s method (Heron yöntemi) olarak da bilinen bu algoritmada, size herhangi bir pozitif S sayısı verilir. S’nin karekökünü bulmak için:
- Önce bir başlangıç tahmini yapın. Pozitif bir S sayısının karekökünü bulmak için herhangi bir pozitif x₀ değeri seçin.
- Sonra tahmini geliştirin. Şu formülü uygulayın: x₁ = (x₀ + S / x₀) / 2. Bu işlemden çıkan x₁, S sayısının kareköküne x₀’a göre daha yakın bir değerdir.
- İşlemi yineleyin. Her adımda: xₙ₊₁ = (xₙ + S / xₙ) / 2 formülünü kullanın. Art arda çıkan sonuçların ondalık basamakları birbirine yaklaştığında işlemi bitirebilirsiniz
Şimdi yöntemi uygulayalım. 20 sayısının karekökünü bulalım:
- İlk tahmini yapalım: x₀ = 10 diyelim. Sonrasında formülü uygulayarak tahmini geliştirelim: x₁ = (10 + 20/10) / 2 = 6
- İkinci adım: x₂ = (6 + 20/6) / 2 = 4,66667
- Bu sonuç hâlâ karekökten uzak. Bu durumda tekrar formülü uygulayalım: x₃ = (4,66667 + 20/4,66667) / 2 = 4,47619
- Bir kez daha geliştirelim: x₄ = (4,47619 + 20/4,47619) / 2 = 4,47214
- Artık son iki sonucun virgülden sonraki iki basamağı aynı. Bu yüzden 20 sayısının karekökünü yaklaşık 4,47 olarak alabiliriz. Bu örnek, Babillilerin yönteminin birkaç adımda ne kadar doğru sonuç verdiğini net biçimde gösteriyor.
Yazının devamında başka karekök algoritmaları için göz atmak isterseniz: Hesap Makinesi Olmadan Karekök Almak İçin İki Basit Yöntem
Kaynaklar ve ileri okumalar için:
- Knuth, Donald Ervin. “Ancient Babylonian algorithms.” Commun. ACM 15 (1972): 671-677.
- Flores, Alfinio. (2014). The Babylonian Method for Approximating Square Roots: Why Is It So Efficient?. The Mathematics Teacher. 108. 10.5951/mathteacher.108.3.0230.
- Ancient Formula Calculate Any Square Root. Kaynak site: Mind your decision. Bağlantı: Ancient Formula Calculate Any Square Root
Matematiksel