İmkânsız gibi görünen basit bir fikirle başlarız: i sayısının karesi −1’dir. Bu küçük ama çarpıcı adım, karmaşık sayıların doğmasına yol açar. Karmaşık sayılar da zamanla matematiğin en güçlü ve en verimli alanlarından biri olan karmaşık analizin temelini oluşturur.
Rönesans İtalya’sı siyaset ve şiddetin yoğun biçimde iç içe geçtiği bir ortamdı. Ülkenin kuzeyi, aralarında birbiriyle savaşan çok sayıda şehir devletinin denetimi altındaydı. Güneyde ise Papalar ile Kutsal Roma İmparatorları üstünlük mücadelesi veriyordu.
Matematik bu ortamda serpilip gelişti. 1545’te kumar tutkunu bir bilgin olan Girolamo Cardano bir cebir kitabı yazarken, onu son derece şaşırtan yeni bir sayı türüyle karşılaştı. Ancak bu sayıları “ işe yaramaz” olarak niteledi ve kavramı bir kenara bıraktı.
Cardano’nun yolundan giden Rafael Bombelli ise 1572’ye gelindiğinde dikkat çekici bir durumu fark etmişti. Bu yeni sayılar anlamlı görünmese de, cebirsel hesaplamalarda kullanılabiliyor ve doğru sonuçlara ulaştırıyordu.
Yüzyıllar boyunca matematikçiler, bugün hâlâ “imajiner (sanal) sayılar” olarak adlandırılan bu kavramlarla çelişkili bir ilişki kurdu. Bunlar, aritmetikte karşılaşılan alışıldık gerçek sayılar değildi. Fakat çoğu bakımdan onlar gibi davranıyorlardı. Temel fark, bir sanal sayının karesinin negatif çıkmasıydı.
Sanal Sayılar Nedir?
Ancak on sekizinci yüzyılda matematikçiler sanal sayıların ne olduğunu açıklığa kavuşturdu. On dokuzuncu yüzyılda ise bu sayıları kullanma konusunda daha rahat davrandılar. Zaman içinde matematikçiler, negatif sayıların kareköklerini düşünmenin ve onlarla işlem yapmanın tutarlı yollarını geliştirmek zorunda kaldı.
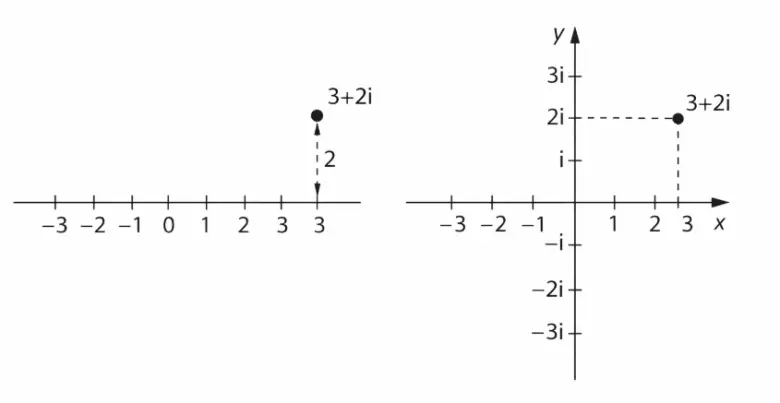
Sanal sayıları anlamlandırmaya çalışan isimlerden biri de İngiliz matematikçi John Wallis’ti. Wallis 1673’te, düzlemde bir doğru çizip bu doğru üzerindeki noktaları alışıldık biçimde gerçek sayılarla eşleştirmeyi, ardından x + iy sayısını bu doğrunun bir tarafında, x noktasından y kadar uzaklıkta bulunan bir nokta olarak görmeyi teklif etti.
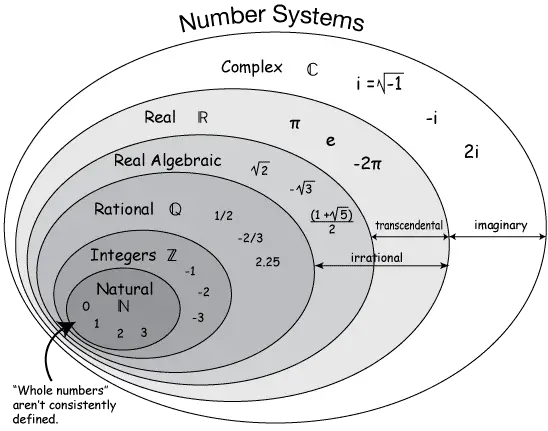
Wallis’in önerisi uzun süre ciddiye alınmadı. Ancak ilerleyen süreçte, Caspar Wessel, Jean-Robert Argand ve Gauss da karmaşık sayıları göstermek için aynı yöntemi kullandı. Gerçek eksene dik ikinci bir eksen tanımladılar ve buna sanal eksen adını verdiler.
Bu geometrik gösterim yararlıydı, ancak karmaşık sayıların neden mantıksal olarak tutarlı bir sistem oluşturduğunu açıklamadı. Onların hangi anlamda “sayı” olduğunu da ortaya koymadı. Yalnızca görselleştirmeyi sağladı. Yine de bu yaklaşım, sanal sayılarla gerçek dünya arasında yapay da olsa bir bağ kurarak psikolojik bir dayanak sundu.
Sanal sayılar ve onların oluşturduğu karmaşık sayı sistemi, bazı öncü matematikçilerin dikkatini karmaşık analiz alanına yöneltmesiyle matematikte sağlam bir yer edindi. Yirminci yüzyılın ikinci yarısına gelindiğinde ise sanal sayılar, her matematikçinin ve bilim insanının zihinsel araç takımının doğal bir parçası hâline gelmişti.
Kuantum mekaniğinin yapısına öylesine temel biçimde yerleşmişlerdi ki, onlarsız fizik yapmak artık imkansızdı. Elektrikli aydınlatmadan dijital kameralara kadar modern teknolojinin büyük bölümü, bu sayılar olmadan geliştirilemezdi.
Sanal Sayılar Ne İşe Yarar?
Sanal sayıları kullanmaya başladığınız zaman, eski sezgilerin doğrudan işlemediği yeni bir alanda olursunuz. Örneğin sinüsün geometrik tanımını kullanamazsınız. Bu nedenle, gerçek sayılar söz konusu olduğunda eski tanımla uyumlu yeni tanımlara ihtiyaç duyarsınız.
Seriler zor görünür ama basit iki fikre dayanır. Birincisi, sayının tam sayı kuvvetlerini almaktır. Bu işlem karmaşık sayılar için de aynen yapılır. İkincisi, sonsuz sayıda terimi toplarken toplamın belli bir değere yaklaşmasıdır. Bu da karmaşık sayılar için geçerlidir.
Yani seride kullanılan işlemler, karmaşık sayılarla da sorunsuz çalışır. Bu yüzden sinüs ve kosinüsü, seri formülleriyle karmaşık sayılar için de tanımlayabiliriz.
- Sinüs için: sin z = z − z³/3! + z⁵/5! − z⁷/7! + …
- Kosinüs için: cos z = 1 − z²/2! + z⁴/4! − z⁶/6! + …
- Üstel fonksiyon: eᶻ = 1 + z + z²/2! + z³/3! + z⁴/4! + …
Bu üç serinin birbirine benzediğini fark etmişsinizdir. Gerçekten de üstel fonksiyonun serisinde z yerine iz yazarsak ve çıkan ifadeyi iki kısma ayırırsak, tam olarak kosinüs ve sinüsün serilerini elde ederiz. Bu seri tanımları şu temel bağıntıyı verir: eiz = cos z + i sin z.
Bu ilişki son derece önemlidir. Yalnızca gerçek sayılarla çalışırken böyle bir bağlantının varlığını tahmin etmek zordur. Karmaşık sayılar bakış açısından ise tablo netleşir ve tüm bu bağlantılar doğal bir bütün oluşturur. Ayrıca matematiğin en güzel denklemlerinden biri neredeyse kendiliğinden ortaya çıkar.
Trigonometrik serilerde z gerçek bir sayı olduğunda açı radyan cinsindendir. Tam bir daire 2π radyandır. Bu nedenle 180° = π radyan olur. Ayrıca sin π = 0 ve cos π = −1’dir. Buradan eiπ = cos π + i sin π = −1 sonucu çıkar.
Sanal birim i, matematiğin en dikkat çekici iki sabiti olan e ile π’yi tek ve son derece yalın bir denklemde bir araya getirir. Bu bağıntı Euler’e atfedilir ve çoğu zaman matematiğin en güzel denklemi olarak anılır.
Sonuç Olarak
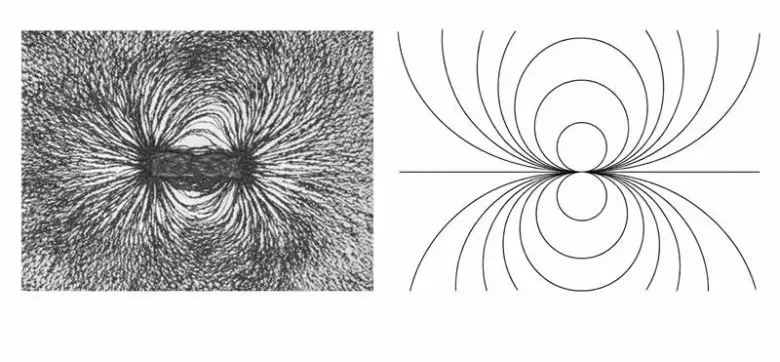
On dokuzuncu yüzyılda matematikçiler karmaşık fonksiyonları ve özelliklerini kullanarak önemli bir adım attı. Karmaşık fonksiyonlar diferansiyel denklemleri çözmede güçlü bir araçtır. Bir fonksiyon f(z) = u(z) + iv(z) biçiminde ayrıldığında, ortaya çıkan iki gerçek fonksiyon fiziksel alanları ve akış çizgilerini tanımlar. Uygun fonksiyon seçimi, manyetizma, elektrik ve akışkan problemlerine doğrudan çözüm verir. Bu yöntem mühendislikte geniş uygulama bulmuştur.
Sonucunda bu güçlü uygulamalar, karmaşık sayıların temeline dair tartışmaları geri plana itti. Yine de zamanla kuramsal açıklama geldi. Hamilton, karmaşık sayıları (x, y) biçiminde iki gerçek sayının sıralı çifti olarak tanımladı. Gerçek sayılar (x, 0), sanal birim i ise (0, 1) olarak yazılır. Toplama ve çarpma için uygun kurallar konduğunda bütün cebir kuralları sağlanır. Böylece x + iy ifadesi yalnızca (x, y) çiftidir.
Karmaşık sayıları etkileyici kılan, özlerinde ne oldukları değil, bu yalın yapıyla ne kadar geniş bir alanı açıklayabildikleridir. Bu anlayış, süregelen felsefi tartışmaları anlamsızlaştırdı ve geriye yalnızca temel gerçek kaldı: i² = −1.
Kaynaklar ve ileri okumalar
- Top 5 facts about Imaginary Math. Yayınlanma tarihi: 26 Ocak 2014. Kaynak site: Big Think. Bağlantı: Top 5 facts about Imaginary Math
- Nikouravan, Misha. (2019). A Short History of Imaginary Numbers. International Journal of Fundamental Physical Sciences. 9. 1-5. 10.14331/ijfps.2019.330121.
- Du, Jie. (2023). The discovery and development of Imaginary number. Highlights in Science, Engineering and Technology. 38. 174-179. 10.54097/hset.v38i.5803.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





