Bir odada belli bir sayıya ulaşıldığında neden en az iki kişinin aynı doğum gününe sahip olma olasılığı %50’yi aşar? Doğum Günü Problemi bu soruya yanıt arar.

İlk bakışta, iki kişinin aynı doğum gününe sahip olma olasılığının oldukça düşük olduğunu düşünebilirsiniz. Gerçekten de, yalnızca iki kişilik bir grupta bu olasılık 1/365’tir. Bunun nedeni basittir: Yılda 365 gün vardır ve ikinci kişinin, birincinin doğduğu günle aynı günde doğmuş olma ihtimali 365’te birdir.
Şimdi, 366 kişilik bir grup düşünelim. Bu durumda, en az iki kişinin aynı doğum gününü paylaşması kaçınılmazdır. Çünkü elimizde yalnızca 365 olası doğum günü vardır ve bu sayı, kişi sayısından küçüktür.
Bu iki örnek yan yana konulduğunda, doğal bir sezgi şu sonuca varabilir: İki kişinin aynı doğum gününü paylaşma olasılığının yüzde 50’ye ulaşması için gereken kişi sayısı bu iki uç noktanın ortalarında bir yerde olmalıdır. Bu nedenle, yaklaşık 180 kişilik bir grupta yüzde 50 olasılığa ulaşacağınızı düşünebilirsiniz. Oysa durum böyle değildir. Gerçekte, bu eşik çok daha küçük bir grup büyüklüğünde ortaya çıkar.

Doğum Günü Problemi Nasıl Çözülür?
Kavramı daha iyi anlamak için basit bir örnekle başlayalım: Ayşe ve Ali. Ayşe’nin doğum gününün 1 Mayıs olduğunu varsayalım. Doğum günlerinin yıl boyunca eşit dağıldığını kabul edersek, Ali’nin doğum gününün de aynı gün olma olasılığı 1/365’tir.
Peki, Ali’nin Ayşe ile aynı doğum gününü paylaşmama olasılığı nedir? Bu, 1 eksi 1/365’tir; yani 364/365. Bu oran, rastgele seçilen ikinci kişinin, ilk kişiden farklı bir doğum gününe sahip olma olasılığını gösterir.
Üçüncü bir kişi eklendiğinde durum biraz değişir. Üç kişinin doğum günlerinin birbirinden farklı olma olasılığı, ilk iki kişinin farklı olma olasılığı (364/365) ile üçüncü kişinin onlardan farklı olma olasılığının (363/365) çarpımına eşittir.
Yani üç kişinin de farklı doğum gününe sahip olma olasılığı (364/365) × (363/365) olur. Grup genişledikçe hesap aynı mantıkla ilerler. Odadaki kişi sayısı arttıkça, içlerinden en az ikisinin aynı doğum gününü paylaşma olasılığı da yükselir. Böylece dört kişilik bir grupta aynı doğum gününü paylaşan iki kişi bulma olasılığı yaklaşık yüzde 1,6 olur.
| Kişi Sayısı | En Az İki Kişinin Aynı Doğum Gününe Sahip Olma Olasılığı |
|---|---|
| 5 kişi | %2,7 |
| 10 kişi | %11,7 |
| 16 kişi | %28,1 |
| 23 kişi | %50,5 |
| 32 kişi | %75,4 |
| 40 kişi | %89,2 |
Kişi sayısı arttıkça bu olasılık hızla yükselir ve görüldüğü gibi, 23 kişilik bir grupta bu olasılık yaklaşık yüzde 50’ye ulaşır.
Neden 23 Kişi?
Yirmi üç kişiyle neden yüzde 50’lik bir eşleşme olasılığına ulaştığımızı merak edebilirsiniz. Bunun temel nedeni, bir grubun içindeki ikili sayısının çok hızlı artmasıdır. Bunu şöyle düşünebilirsiniz:
Birinci kişi, odadaki diğer 22 kişiyle ikili oluşturabilir. İkinci kişi, kendinden önce saydığımız birinci kişiyle zaten ikili oluşturdu, bu yüzden geri kalan 21 kişiyle yeni ikililer oluşturabilir. Üçüncü kişi, 20 yeni ikili ekler.
Böyle devam eder.
Yani toplam ikili sayısı şöyle oluşur: 22 + 21 + 20 + 19 + … + 1. Bu sayıların toplamı da 253 eder. Bu 253 ikilinin her biri, aynı doğum gününe sahip olma olasılığı taşır. Bu olasılık tek bir ikili için düşüktür (1/365). Ancak 253 kez denendiği için eşleşme ihtimali bir anda yükselir ve yüzde 50’yi aşar.
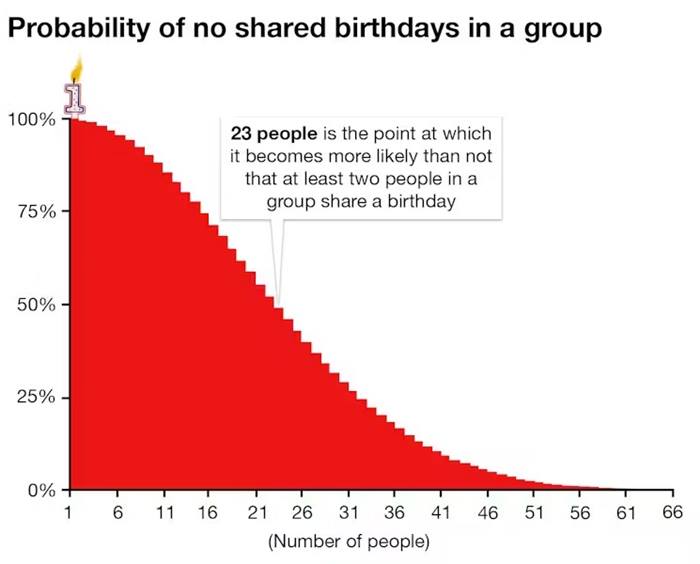
Paradoksun temel nedeni şudur: Soru sizin belirli doğum gününüzü paylaşma olasılığını sormaz. Soru, gruptaki herhangi iki kişinin aynı doğum gününe sahip olup olmadığını araştırır. Bu ayrım çok önemlidir.
Yirmi üç kişilik bir grupta bunu düşünelim. Siz de odadasınız. Sizinle eşleşme ihtimali olan yalnızca 22 kişi vardır. Bu nedenle bir kişinin sizin doğum gününüzü paylaşma olasılığı yüzde 50’ye yaklaşmaz; yalnızca yaklaşık yüzde 6’dır.
Sonuç Olarak
Bu sonuç şaşırtıcı görünür, çünkü küçük bir grupta bile eşleşme için düşündüğümüzden çok daha fazla fırsat vardır. Örneğin bir futbol maçının başında sahadaki yirmi iki oyuncunun ve hakemin doğum günlerini öğrenseniz, çoğu zaman iki kişinin aynı güne denk geldiğini görürsünüz.
Bu düşüncenin kullanım alanı doğum günleriyle sınırlı değildir. Bilgisayar sistemlerinin güvenliği ve performansı için de önemlidir. Verilerin beklenmedik biçimde çakışması, ciddi hatalara yol açabilir. Bu paradoksun mantığını kavramak, bu tür sorunları öngörmek ve engellemek için gereklidir. Bu sayede sistemler daha sağlam ve verimli çalışır.
Paradoksun eğlenceli yanı ise günlük yaşamda ortaya çıkar. Arkadaşlarınızla bir araya geldiğinizde bu konuyu açabilirsiniz. Çoğu zaman küçük bir grubun içinde bile doğum günlerinin nasıl çakıştığını görmek, olasılığın ne kadar şaşırtıcı olabileceğini hemen gösterir.
Kaynaklar ve ileri okumalar:
- Paradoxes of probability and other statistical strangeness. Yayınlanma tarihi: 4 Nisan 2017. Kaynak site: Conversation. Bağlantı: https://doi.org/10.64628/AA.nryed7379
- What is the birthday paradox?; yayınlanma tarihi: 30 Temmuz 2022; Kaynak site: L,ive Sceince. Bağlantı: What is the birthday paradox?
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





