Kaos Teorisi, doğası gereği tahmin edilemeyen sistemlerin nasıl davrandığını inceleyen bir bilim dalıdır. İnsan kalbinin ritminden gökyüzündeki asteroitlerin rotasına kadar uzanan birçok karmaşık doğa olayının ardındaki dinamikleri anlamamıza yardımcı olur.

19. yüzyılda yaşayan Fransız matematikçi Pierre Laplace, 1814 yılında kaleme aldığı bir yazısında dikkat çekici bir iddiada bulunmuştu: Eğer evrendeki tüm parçacıkların konumunu ve hızını kesin olarak bilebilseydik, gelecekte olacak her şeyi tam isabetle öngörebilirdik. Ona göre bir gün hava durumu tahminlerinden gezegen hareketlerine kadar her şey, kusursuz bir biçimde hesaplanabilecekti.
Isaac Newton ise evreni bir saat mekanizması gibi işleyen, belirli fizik kurallarıyla yönetilen bir sistem olarak görüyordu. Ancak Kaos Teorisi, en kesin fizik kurallarının bile bazen öngörülemeyen sonuçlar doğurabileceğini ortaya koyar. Çünkü gerçek dünyada olaylar her zaman düz bir çizgide ilerlemez; birçok şey rastlantısal gibi görünür. Ancak burada önemli bir ayrım vardır: kaos ve rastgelelik aynı şey değildir.
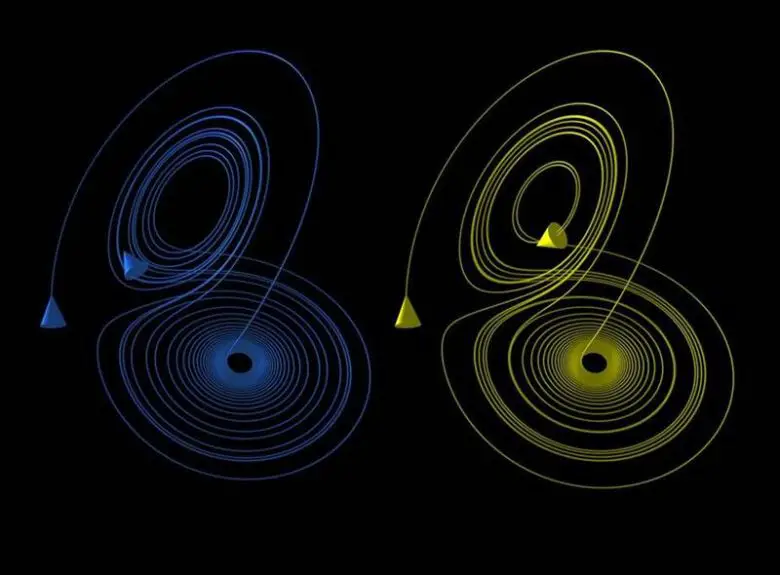
Kaos, tam rastgelelikle tamamen tahmin edilebilirlik arasında bir noktada yer alır. Bu teorinin kalbinde ise oldukça ilgi çekici bir düşünce yatıyor: Düzen ile kaos her zaman birbirine zıt kavramlar değildir. Aslında kaotik sistemler, hem düzenli hem de düzensiz özellikler taşıyan karmaşık yapılardır. Dahası, 1960’lar ve 70’lerde yapılan birçok bilimsel çalışma, kaosun oluşumunun ne denli kolay olduğunu gözler önüne sermiştir.
Kaos Teorisi Nedir?
Kaos teorisi, başlangıç koşullarına son derece duyarlı dinamik sistemlerin davranışlarını açıklar. Hava durumu buna klasik bir örnektir. Bir ay ya da bir yıl sonrası için hava tahmini yapabilmek elbette harika olurdu, ancak bu sistemlerin doğası gereği bazı temel zorluklar içerir.
Bu zorlukların nedeni, yalnızca süreçlerin karmaşıklığı değil; aynı zamanda yaşadığımız evrenin büyük ölçüde öngörülemez ve kaotik bir yapıya sahip olmasıdır. Kaotik sistemler genellikle basit matematiksel denklemlerle tanımlanır. Fakat bu denklemlerdeki küçük bir değişiklik bile sonuçların tamamen farklılaşmasına yol açar.
Fiziğin büyüleyici yönlerinden biri deterministik olmasıdır. Yani bir sistemin tüm özelliklerini ve fizik yasalarını biliyorsanız, geleceğini teorik olarak kusursuz biçimde öngörebilirsiniz. Ancak kaos teorisi, bir sistemin deterministik olmasına rağmen yine de öngörülemez davranışlar sergileyebileceğini gösterdi.
Üç cisim problemi, 1800’lerde İsveç Kralı’nın Güneş ve iki gezegenin hareketlerini kesin olarak tahmin edebilecek kişiye ödül vaat etmesiyle gündeme geldi. Bu ödül, Fransız matematikçi Henri Poincaré’ye verildi. Poincaré, problemi doğrudan çözemese de, bu tür sistemlerin neden kesin olarak çözülemeyeceğini gösterdi.
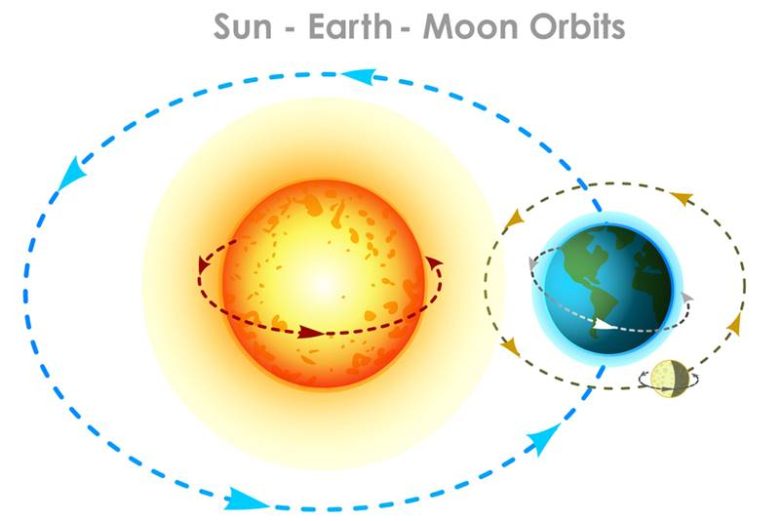
En önemli bulgusu, başlangıç koşullarındaki en küçük farklılıkların zamanla büyük ve öngörülemez sonuçlara yol açabileceğiydi. Bu fikir, kaos teorisinin temellerini atan en erken bilimsel işaretlerden biri oldu.
Ancak Poincaré’nin çalışmaları, döneminde hak ettiği ilgiyi görmedi. Kaos teorisi, ancak 1963 yılında Edward Lorenz’in hava durumu simülasyonları sırasında, çok küçük girdilerdeki değişimlerin dramatik sonuçlara yol açabileceğini fark etmesiyle geniş kitlelerin dikkatini çekti.
Kaos Teorisi İle Nasıl Tanıştık?
1961’de MIT’den meteorolog Edward Lorenz, hava durumu tahmini için geliştirdiği bir bilgisayar modeline veriler giriyordu. Modelde kullanılan değişkenlerden birinin değeri 0.506127 idi. Lorenz modeli yeniden çalıştırırken bu değeri 0.506 olarak yuvarladı ve kahve almak için odadan çıktı. Döndüğünde, küçücük bir farkın tahminleri tamamen değiştirdiğini gördü.

Lorenz, 1972’de Amerikan Bilimin Gelişmesi Derneği toplantısında bu konuyu anlattığında ünlü sorusunu sordu. “Brezilya’da bir kelebeğin kanat çırpması, Teksas’ta bir kasırgayı tetikler mi?”
Bu bulgu, uzun vadeli hava tahminlerinin asla tamamen güvenilir olamayacağını gösterdi. Çünkü başlangıç koşullarındaki küçücük hatalar bile zamanla büyüyerek, tahminlerin ciddi şekilde sapmasına yol açıyordu. Başka bir deyişle, hava durumu hesaplamalarında mutlak kesinlik yalnızca bir hayaldi.
Lorenz Çekicisi Nedir?
Lorenz yalnızca kaosu keşfetmekle kalmadı. Aynı zamanda kaotik davranışın nasıl ortaya çıktığını gösteren temel mekanizmayı da ortaya koydu. Verilerini farklı eksenlerde grafik haline getirdiğinde, dikkat çekici bir durumu fark etti.
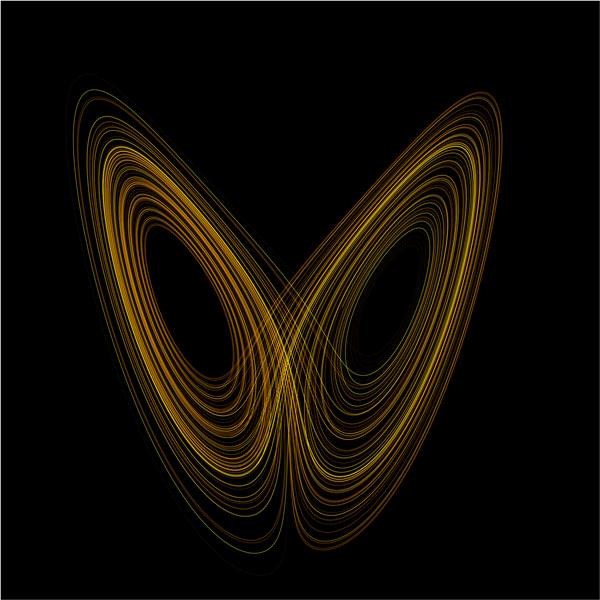
Zaman içinde birbirine çok yakın başlayan iki nokta, her adımda birbirinden uzaklaşıyor, aralarındaki fark giderek büyüyordu. Birkaç tekrar (iterasyon) sonrasında bu iki nokta, başlangıçta neredeyse aynı yerde olmalarına rağmen, tamamen farklı sonuçlara ulaşıyordu. Sanki başlangıçtaki küçük bir fark, zamanla büyüyüp tamamen ayrı dünyalara sürüklüyordu.
Ancak ilginç bir şekilde, sistemin dışında kalan noktalar, tekrarlandıkça bu yapıya doğru çekiliyordu. Bu yapı, bilim insanları tarafından “garip çekici” olarak adlandırıldı. Lorenz’in keşfettiği özel yapıya ise “Lorenz çekicisi” dendi.
Kısa süre sonra başka garip çekiciler de keşfedildi. Bunlar arasında en dikkat çekeni, 1976 yılında Fransız matematikçi Michel Hénon tarafından tanımlanan Hénon çekicisidir. Bu tür çekiciler, Fransız-Polonyalı matematikçi Benoît Mandelbrot tarafından “fraktal” olarak adlandırılan kendine benzer (self-similar) yapılar sergiler.

Bir garip çekiciyi haritalandırdığınızda, yakınlaştırılan herhangi bir bölge, yapının tamamına oldukça benzer bir görünüm sunar. Aynı şekilde, bu bölgenin daha da küçük bir parçası büyütüldüğünde yine benzer bir desen ortaya çıkar. Bu tekrar eden örüntü, ölçek küçüldükçe de devam eder. Matematiksel olarak bu durum, yapının tam sayı olmayan yani kesirli bir boyuta sahip olduğunu gösterir.
Sonuç Olarak
Lorenz’e, Laplace’ın determinist evren anlayışındaki temel bir yanılgıyı ortaya çıkardığı için çok şey borçluyuz. Newton’un klasik mekaniği, evrenin bütünüyle öngörülür olduğunu ileri sürerken, Lorenz bazı sistemlerin başlangıç koşullarına olağanüstü derecede duyarlı olduğunu gösterdi. Bu duyarlılık, uzun vadeli tahminlerin neredeyse imkânsız hale gelmesine yol açtı.
Kaynaklar ve ileri okumalar:
- Chaos Theory, The Butterfly Effect, And The Computer Glitch That Started It All. Yyaınlanma tarihi: 13 Şubat 2018. Kaynak site: Forbes. Bağlantı: Chaos Theory, The Butterfly Effect, And The Computer Glitch That Started It All
- Explainer: what is Chaos Theory? Yayınlanma tarihi: 19 Kasım 2012. Kaynak site: Conversation. Bağlantı: Explainer: what is Chaos Theory?
- Oestreicher C. A history of chaos theory. Dialogues Clin Neurosci. 2007;9(3):279-89. doi: 10.31887/DCNS.2007.9.3/coestreicher. PMID: 17969865; PMCID: PMC3202497.
- Chaos theory explained: A deep dive into an unpredictable universe. Yaınlanma tarihi: 19 Kasım 2022. Kaynak site: Space. Bağlantı: Chaos theory explained: A deep dive into an unpredictable universe
- Adewumi, Aderemi & Kagamba, Jimmy & Alochukwu, Alex. (2016). Application of Chaos Theory in the Prediction of Motorised Traffic Flows on Urban Networks. Mathematical Problems in Engineering. 2016. 1-15. 10.1155/2016/5656734.
Matematiksel





