Çözmesi zor fakat anlatması şaşırtıcı derecede kolay olan paradokslar oldukça nadirdir. İki zarf paradoksu ya da değişim problemi, bu istisnai örneklerin başında gelir.

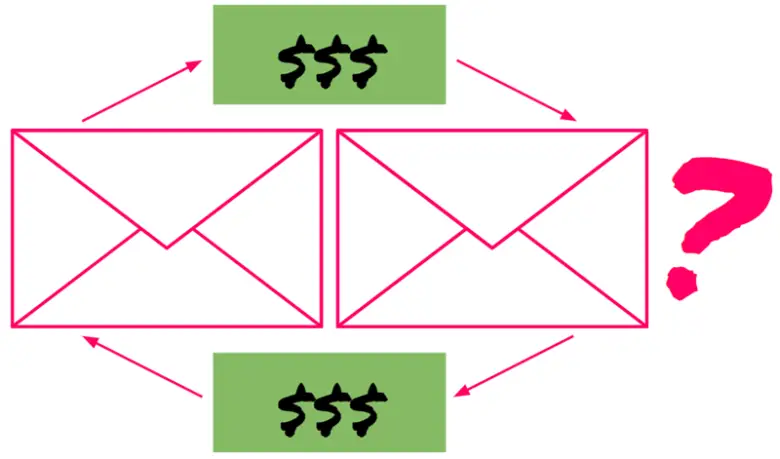
Bu paradoksta, zengin amcanız önünüze iki zarf koyar. Zarflardan birinde, diğerinin iki katı kadar para olduğunu söyler; ancak hangisinde daha fazla para bulunduğunu belirtmez. Ardından, istediğiniz zarfı seçip içindekileri alabileceğinizi ifade eder.
Peki, paradoks nerede başlar? Şimdi, Zarf 1’i seçtiğinizi ve içinde beş yüz dolar bulunduğunu hayal edin. Tam bu sırada, amcanız fikrinizi değiştirip Zarf 2’yi seçebileceğinizi söyler. Böylece kritik bir soruyla karşılaşırsınız: Zarfı değiştirmeli misiniz? Değiştirirseniz, beklenen kazanç ne olur? Ve “beklenen kazanç” dediğimizde tam olarak neyi kastederiz?
Beklenen Değer Nedir?
Olasılık kuramında, beklenen değer kavramı basit ama son derece önemlidir. Rastlantısal bir süreçte elde edilebilecek tüm sonuçlar, her birinin gerçekleşme olasılığıyla çarpılır ve bu değerler toplanarak beklenen değer hesaplanır.
Örneğin, bir kumarhane çarkı çevirmek için oyuncudan 40 dolar alsın. Çarkı çeviren kişi kazanırsa 1.000 dolar, kaybederse 10 dolar alacaktır. Kazanma olasılığı 0,02 olduğuna göre, kaybetme olasılığı 0,98 olur. Bu durumda, oyuncunun bir çevirme başına beklenen kazancı (ücret hariç) şu şekilde hesaplanır:
Beklenen kazanç = 1.000 × 0.02 + 10 × 0.98 = 29.80 dolar.
Buradan, çarkı çevirme ücreti olan 40 dolar çıkarıldığında, oyuncunun beklenen kazancı –10,20 dolar olur. Yani oyuncu, her çevirmede ortalama 10,20 dolar kaybetmeyi beklemelidir.
Şimdi, iki zarf problemine geri dönebiliriz. Amcanız, zarflardan birinde diğerinin iki katı para olduğunu söyledi; ancak hangi zarfta daha fazla para olduğunu bilmiyoruz. Birinci zarfta 500 dolar bulunduğuna göre, ikinci zarf ya 250 dolar ya da 1.000 dolar içerebilir ve her iki olasılığın gerçekleşme ihtimali 1/2’dir. Bu durumda, ikinci zarfa geçerseniz beklenen kazancınız şu şekilde hesaplanır:
Beklenen kazanç = 250 × (1/2) + 1.000 × (1/2) = 625 dolar.
Bu da, 125 dolarlık bir artış anlamına gelir. Genel durumda, birinci zarfta D dolar olduğunu varsayalım. Bu durumda, ikinci zarfa geçerseniz beklenen kazancınız şu şekilde hesaplanır:
Beklenen kazanç = (D/2) × 0,5 + (2D) × 0,5 = (5/4) × D
Bu da, ilk seçtiğiniz zarfın değerine göre D/4 kadar bir artış sağlar. Öyleyse hangisini önce seçtiğinizin bir önemi kalmaz; çünkü her zaman diğer zarfa geçmek daha kârlı görünür.
Şimdi, zarfı hiç açmadığınızı ve içindeki miktarı bilmeden değiştirme şansınız olduğunu varsayalım. Beklenen değerin 5D/4, yani 1,25D olduğunu düşünürsek, ikinci zarfın beklenen değerinin birinci zarfa göre yüzde 125 olduğunu görürüz. Yani yalnızca zarf değiştirerek para kazanmak mümkün görünmektedir.
Ancak ortada açık bir çelişki vardır. Eğer iki zarf da sonlu miktarda para içeriyorsa, bu durumda beklenen değerin sürekli artması mümkün değildir. Yine de yapılan hesaplar doğru görünüyor. Bu da insanı şu soruya götürür: Eğer matematik bunu gösteriyorsa, sonuç nasıl yanlış olabilir?
İki Zarf Problemi İle İlgili Sorun Nedir?
Sorunu görmek için beklenen değer hesabına yeniden bakmak gerekir. Bu noktadaki hata çoğu zaman fark edilmez, çünkü hesap doğru gibi görünür. Ancak buradaki sıkıntı şudur:
Hesapta geçen iki farklı D değeri aslında aynı şeyi temsil etmez. İlk durumda, ikinci zarfta 2D para olduğunu varsayarız. Bu, elimizdeki zarfın daha küçük olduğunu kabul ettiğimiz içindir. İkinci durumda ise ikinci zarfta D/2 para olduğunu varsayarız. Bu kez de elimizdeki zarfın daha büyük olduğunu kabul etmiş oluruz.
Dolayısıyla, hesapta kullanılan D değerleri aynı değildir. Bu karışıklık, beklenen değer hesabını hatalı gösterir.
Bu durumu daha iyi anlamak için farklı bir bakış açısı geliştirebiliriz. İki zarftaki toplam para miktarının 3D olduğunu varsayalım. Küçük zarf D, büyük zarf ise 2D içerir. Tüm olasılıkları net bir şekilde anlamak için bir olasılık ağacı çizelim.
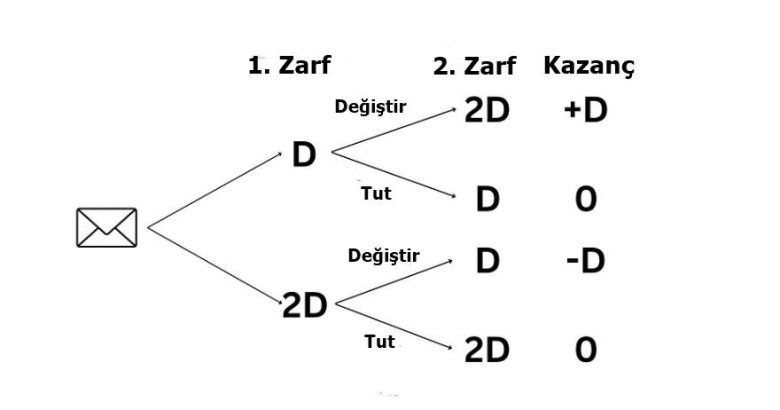
Bu durumda, zarf değiştirdiğinizde D kazanma olasılığınız yüzde 50, D kaybetme olasılığınız da yine yüzde 50 olur. İçgüdünüzün de işaret ettiği gibi, uzun vadede zarf değiştirmek toplam kazancı etkilemez.
Sonuç Olarak
Zarfı değiştirmek size ne bir avantaj sağlar ne de bir kayba yol açar. Matematiksel hesaplara başvurmadan önce, akla en yatkın görünen sonuç da zaten budur. Bu paradoks, bazı hesaplamaların sezgilerimizi nasıl yanıltabildiğini açıkça gösterir. Bazen matematiksel olarak doğru görünen bir sonuç, bizi gerçeğe hiç yaklaştırmaz.
Okumak isterseniz: Monty Hall Problemi: Kapıyı Değiştirmek Neden Kazanma Şansınızı İki Katına Çıkartır?
Kaynaklar ve ileri okumalar
- Abbott, Derek & Davis, Bruce & Parrondo, Juan MR. (2010). The two-envelope problem revisited. Fluctuation and Noise Letters. 23. 1-8. 10.1142/S0219477510000022.
- Maths in a minute: The two envelopes problem. Yayınlanma tarihi: 26 Eylül 2017; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel