Kökleri antik döneme uzanan Josephus Problemi, matematiksel ve algoritmik düşünmeyi sınayan klasik bir bulmacadır. Birinci yüzyılda yaşayan Yahudi tarihçi Josephus’un bu problemi doğru çözerek hayatını kurtardığı söylenir.

Flavius Josephus, Kudüs aristokrasisine mensup bir Yahudi tarihçiydi. MS 64 yılında Roma’da rehin tutulan bazı Yahudi rahiplerinin serbest bırakılması için İmparator Neron ile görüşmek üzere Roma’ya gitti. Bu dönemde Neron, Yahudi isyanını bastırma görevini General Vespasian’a vermişti.
Vespasian’ın komutasındaki Roma ordusu, Josephus ve kırk arkadaşını Jotapata adlı dağ kasabasında kuşatmaya aldı. Kuşatma sırasında Josephus ve adamları bir mağarada sıkıştı. Bu olay, Josephus Problemi’nin doğduğu tarihsel bağlam olarak anlatılır.
Josephus Problemi Nedir?
Hikâyeye göre Josephus ve kırk arkadaşı, Roma’ya teslim olup köleleştirilmektense topluca intihar etmeye karar verir. Ancak bunu rastgele yapmak istemezler. Belirli bir düzen kurarlar. Herkes bir çember oluşturacak biçimde dizilir. Sayma bir yönde ilerler. Her üç kişiden biri öldürülecektir. Birinden başlanır, “bir, iki, üç” denir ve üçüncü kişi öldürülür. Sonra sıradaki kişiden yeniden sayılır. Bu düzen, çemberde yalnızca iki kişi kalana kadar sürer.
Efsane, Josephus’un bu ölümcül oyunda matematiğini kullandığını anlatır. Hayatta kalacağı pozisyonu önceden hesaplar. Sıralamanın sonunda yalnızca kendisi ve bir kişi daha kalır. O kişiyi teslim olmaya ikna eder ve böylece kurtulur.

Sorunun özü burada belirir. Josephus çemberde tam olarak nereye durmuştu? Hangi başlangıç pozisyonu seçilirse son kişi hayatta kalır? Josephus Problemi tam da bu soruyu yanıtlamaya çalışır.
Josephus Problemi uzun süredir matematikçilerin, bilgisayar bilimcilerinin ve bulmaca meraklılarının dikkatini çeker. Temel düşünce aslında basittir. Bir çemberde n kişi oturur ve her k’inci kişi elenir. Bu işlem, geriye tek bir kişi kalana kadar sürer. Sorulansa nettir. En son kalan kişi hangi sırada oturur?
Örneğin k = 2 olsun. Birden n’ye kadar numaralanmış kişiler bir çember oluşturur. Sayma birinci kişiden başlar. Her iki kişiden biri elenir. Bu döngü, n−1 kişi elenene kadar devam eder. Sonunda tek kişi hayatta kalır. Bu kişinin numarasını bulmak gerekir.
Bu soru basit görünür ama sayma, döngüsel yapı ve örüntü keşfi gibi temel düşünme becerilerini sınayan klasik bir problem olmayı sürdürür.
Josephus Problemi Nasıl Çözülmelidir?
Çözümü sadeleştirmek için sayıyı düşürmek iyi bir başlangıç sağlar. Bu nedenle 41 kişi yerine 8 kişiyle aynı düzeni inceleyelim. Kurala göre her iki kişiden biri ölüyor. Başka bir anlatımla herkes yanındaki sağ komşusunu öldürüyor.
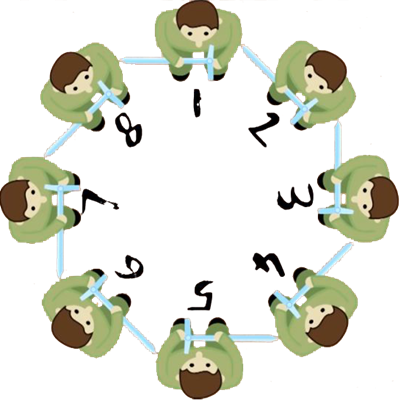
Birinci kişiden başlarız. Birinci kişi ikinci kişiyi öldürür. Üçüncü kişi dördüncü kişiyi öldürür. Beşinci kişi altıncı kişiyi öldürür. Yedinci kişi sekizinci kişiyi öldürür. İlk turun sonunda dört kişi kalır. Bunlar birinci, üçüncü, beşinci ve yedinci kişilerdir.
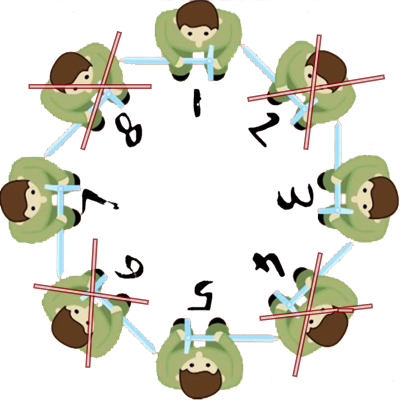
Çember daralır ve sayma yeniden başlar. Birinci kişi üçüncü kişiyi öldürür. Beşinci kişi yedinci kişiyi öldürür. Artık iki kişi kalır. Birinci ve beşinci kişiler. Son tur başlar. Birinci kişi beşinci kişiyi öldürür. Hayatta kalan tek kişi birinci kişidir.
Bu örnekten çıkan sonuç açıktır. Josephus sekiz kişilik çemberde hayatta kalmak için bir numarada durmalıdır. Son aşamada beş numaralı kişiyle karşı karşıya kalır. Onu ikna eder ya da öldürerek oyunu bitirir. Şimdi bu gözlemi genelleştirelim. Asker sayısını n ile gösterelim. Hayatta kalan kişinin numarasını J(n) olarak tanımlayalım. Şimdi iki ayrı durumu incelemek gerekir.
Çift Sayıda Asker Varsa
Asker sayısı yani çift olduğunda herkes sağındaki kişiyi öldürür. İlk tur sonunda hayatta kalanlar birer atlayarak sıralanan kişilerdir. Bu kişiler eski numaralarının yarısına denk düşen yeni bir dizilim oluşturur. Bu nedenle n çift olduğunda J(n) için şu ilişki geçerlidir: J(n) = 2 J(n/2) − 1.
Tek Sayıda Asker Varsa
Ancak n tek olduğunda birinci turun sonunda tek kişi artar ve yapı hafifçe kayar. Sayma bir tur döner ve bir kişi öldükten sonra n−1 kişilik yeni bir çember oluşur. Bu çember artık çifttir. Bu nedenle n tek olduğunda şu ilişki ortaya çıkar: J(n) = 2 J((n−1)/2) + 1. Buradaki artı bir, döngünün tek kişiden kaynaklanan kaymasını ifade eder.
Şimdi bir tablo oluşturalım. Bu tablo, on beş kişiye kadar hayatta kalmak için seçilmesi gereken pozisyonu gösterir. Sekiz kişi için bir numaranın doğru olduğunu yukarıda gördük. Diğer sayılar için de çember çizip aynı yöntemi izleyerek sonucu doğrulayabilirsiniz.
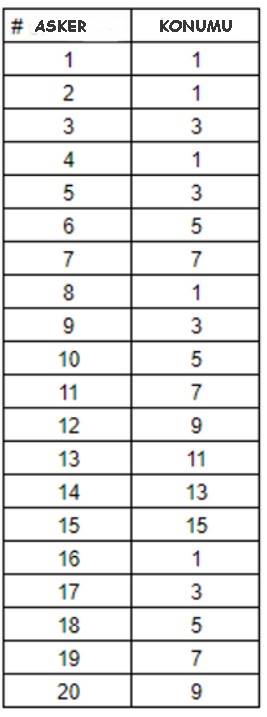
Tablodaki örüntü dikkat çekicidir. Bir numarada hayatta kalan kişilerin karşısında iki sayısının kuvvetleri bulunur. Bu nedenle asker sayısı otuz iki olduğunda hayatta kalan yine bir numaralı kişi olur.
Başlangıçtaki problemde kırk bir kişi vardı. Kırk bire en yakın iki üssü otuz ikidir. Bu noktadan sonra sayarak çözümü adım adım çıkarabiliriz. Otuz üçüncü asker üç numaraya, otuz dördüncü asker beş numaraya, otuz beşinci asker yedi numaraya denk gelir.
Bu biçimde saymaya devam edersek kırk birinci asker on dokuzda durursa hayatta kalır. Bu nedenle Josephus’un son kalan olmak için on dokuzuncu konumu seçmesi gerekir.
Yazının bitiminde ayrıca göz atmak isterseniz: Sahte Para Bulmacası İle Matematiksel Gerçekliği Arayalım
Kaynaklar ve ileri okumalar
- The Josephus Problem – Numberphile. Yayınlanma tarihi: 28 Ekim 2016; Bağlantı: https://www.youtube.com
- Park, Jang-Woo & DOGAN, Ali & Teixeira, Ricardo. (2021). Block Josephus Problem: When the Reality is More Cruel Than the Old Story. Hacettepe Journal of Mathematics and Statistics. 50. 1-12. 10.15672/hujms.750167.
Matematiksel