“Hareket yasaları ve ondan türetilenler veya başka şekilde gözlenenler esasında doğanın aynı esaslarına dayanır. Hayvanların hareketlerini, bitkilerin büyümelerini gözlemlediğimizde hepsi en az eylem ihtiyacının bir sonucudur.” – Pierre Louis Maupertuis.

Maupertuis En Az Eylem İlkesinin evrenin yasalarını birleştireceğine inanıyordu. Benzer düşünceler içinde olan diğer bilim insanları da bu ekonomi ilkesini geliştirmek ve genellemek için yoğun çabalar sarf etmeye başlamışlardı. Bu süreçte Joseph-Louis Lagrange (1736–1813), en az eylem ilkelerine temel teşkil edecek nitelikteki matematiksel yaklaşımları geliştirmiştir.
En Az Eylem İlkesi Nedir?
En az eylem ilkesi Maupertuis’in öncü çalışmasından yaklaşık 100 yıl sonra matematikçi Sir William Rowan Hamilton’un elinde nihai şeklini almıştır. Bu nedenle en az eylem ilkesinin bir diğer adı da Hamilton İlkesidir. Kendisi bu ilkeyi ele alırken temelinde eylemi sonsuz küçük süre boyunca bu süre çarpı parçacığın Lagrangian fonksiyonu olarak tarif etmişti. Fiziksel bir sistemin S ile gösterilen eylemi, zamanın iki anı (t1 ve t2) arasındaki Lagrangian’ın integrali olarak tanımlanır .
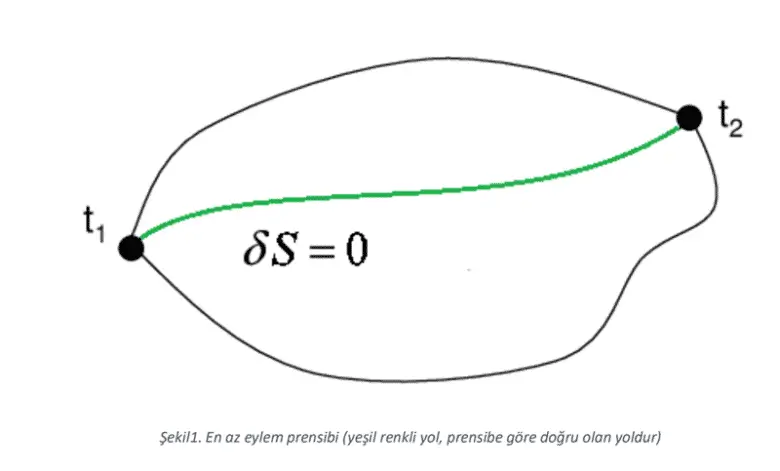
En az eylem ilkesi, herhangi bir cismin uzaydaki bir noktadan diğerine gitmek için mümkün olan olası yörüngeler arasında eylem artışının en az olacağı yörüngeyi seçeceği savı üzerine dayanır. İlkenin önemi, fiziksel kanunları Euler-Lagrange denkleminin bir uç nokta çözümü olarak ifade etmesidir. Peki ama tam olarak ne demek istiyoruz?
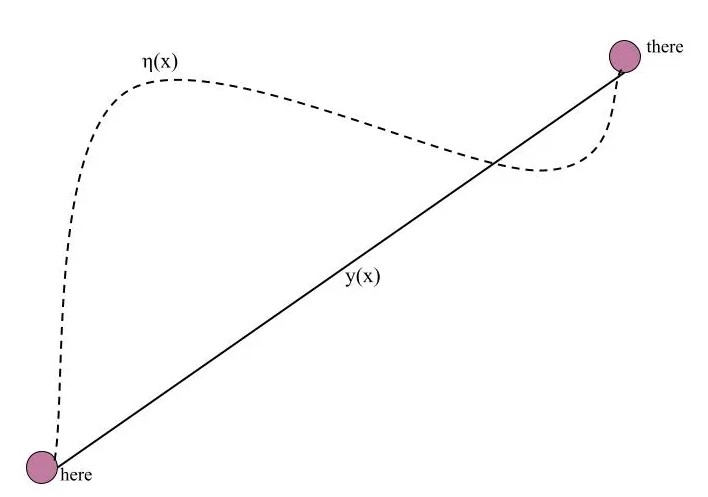
Diyelim ki bir yerden başlayıp başka bir noktaya hareket eden ve y(x) yörüngesini takip eden bir parçacığınız var. Bu iki nokta arasındaki mesafeyi belli bir zamanda alıyor. Şimdi aynı parçacığın aşağıda gördüğünüz gibi farklı bir yörüngede gittiğini ama aynı zamanda vardığını düşünelim. Şimdi yolun her anındaki kinetik enerjiyi hesaplarsanız, sonuçtan potansiyel enerjiyi çıkarırsanız elde edeceğiniz sayının ilkinden daha büyük olduğunu göreceksiniz.
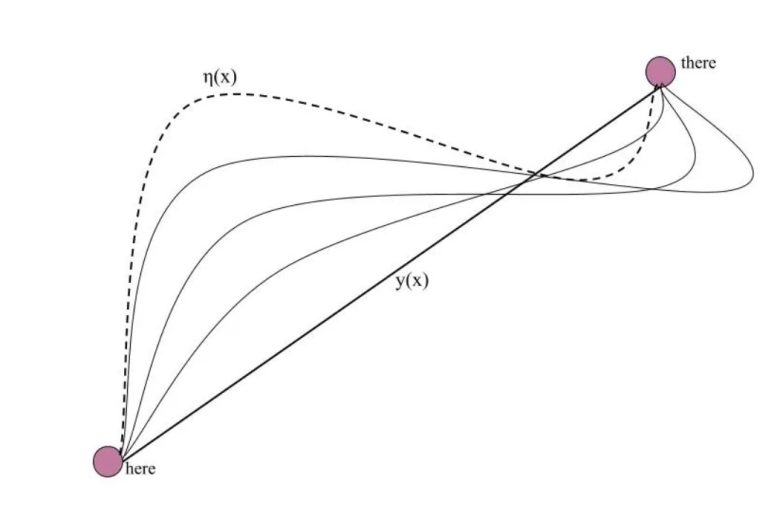
En az eylem ilkesi bu mantığa dayanmaktadır. Süslü bir L ile gösterilen Lagrangian, sistemimizin kinetik enerji bileşenlerinden potansiyel enerji bileşenlerinin çıkarılmasıyla tanımlanır. Şimdi aşağıdaki şekle bakalım. Bu sefer parçacığımız için bir çok yol olduğunu düşünelim. Şekilde y(x) en kısa yolu temsil ediyor. Burası eylemin türevinin sıfır değerini aldığı optimal yoldur.
Sistemler karmaşıklaştıkça eylemlerinin hesaplanması da karmaşıklaşır. Bu nedenle, çoğu zaman bu kadar basit fikirlerle karşılaşmayacaksınız. Bu gibi durumlarda da eylemi s olarak düşünürseniz aşağıdaki formülü kullanmak gerekecektir.
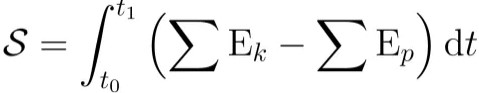
En Az Eylem İlkesi En Kısa Yolun Bulunması İle İlgilidir
Yukarıda formüllere fazla girmeden kısaca aktarmaya çalıştığımız en az eylem ilkesini günlük yaşamda çoğu zaman fark etmeden uygularız. Bir sahilde cankurtaran olduğunuzu hayal edin. Etrafı gözlemlerken bir bakıyorsunuz birisi boğuluyor. En kısa yoldan boğulan kişinin yanına gitmeniz gerek fakat bir sorun var.
Dümdüz kumdan koşarak mı gitmelisiniz yoksa kenardaki beton yoldan mı? Beton yol tam olarak boğulan kişinin olduğu yere gitmiyor. Fakat kumda koşmak da pek kolay değil, zaman alıyor. Bu durumda ne yaparsanız en kısa yoldan boğulan kişinin yanına gidebilirsiniz?
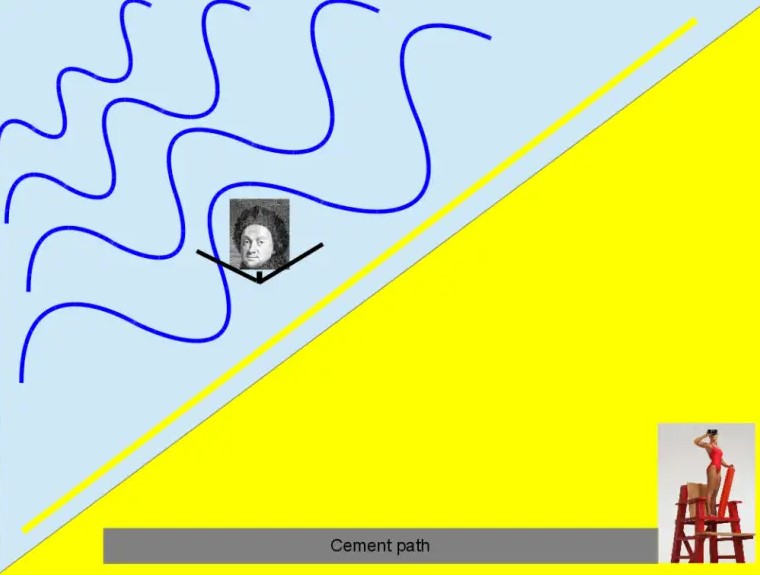
Aslında bu durumda en doğru tercih biraz kumda biraz da beton yolda koşmak olacaktır. Çünkü bu sayede boğulmakta olan kişiye en kısa sürede ve en kısa yoldan ulaşabilirsiniz. Aslına bakarsanız Snell yasası ismini verdiğimiz kırılma kurallarıyla cankurtaran örneğimiz arasında da bir benzerlik kurabilirsiniz.
Bu yasaya göre ışık her ortamda aynı hızda ilerlemez. Yoğun ortamlarda yavaşlar. Bu nedenle ortam yoğunluğu farklılaştığında ışık kırınıma uğrar ve aynı yolu izleyemez. Görselde de gördüğünüz gibi ışık, az yoğun ortamdan çok yoğun ortama geçtiğinde kırılır. Bunun sebebiyse ışığın en kısa yolu izlemek istemesidir.
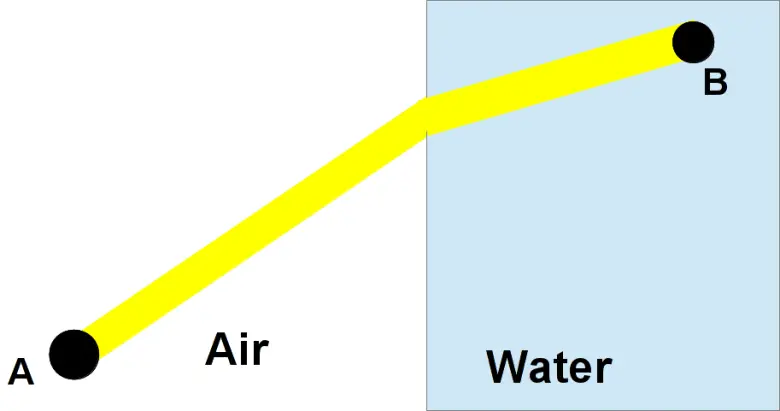
Cankurtaran en kısa mesafeyi kendisi isteyerek, kendi aklıyla seçti. Peki bir foton bunu nasıl yapıyor? Bir fotonun en kısa mesafeyi alma eğilimi de en az eylem prensibidir.
En Az Eylem İlkesi Uygulamaları
Kuantum mekaniği 1926’da Erwin Schrödinger’in dalga fonksiyonunun zamana göre değişimi gösteren ve kendi adını taşıyan Schrödinger denklemini ortaya atmasıyla çığır atmıştı. Sonraki 10 yılda Paul Dirac da kuantum dünyasında alternatif bir vizyon geliştirdi.
Dirac’ın fikirleri bir şeyin A noktasından B noktasına en kısa yoldan gitmesini açıklayan en az eylem prensibinin genel anlamda en az enerji ve en az zaman harcayan versiyonuna dayanıyordu. Daha sonra Richard Feynman, Dirac’ın bu çalışmalarını keşfetti. Ve 1948’de Feynman yol integralini ortaya attı.

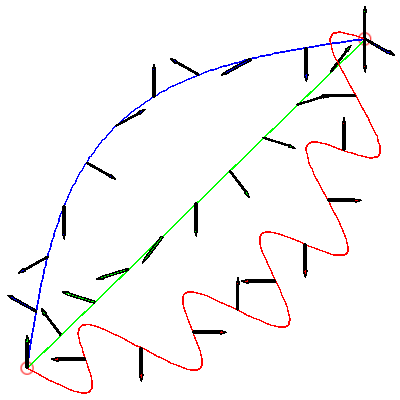
Klasik fizikte bir parçacık A noktasında B noktasına gideceği zaman iyi tanımlanmış tek bir yolu izler. Ancak kuantum mekaniğinde durum çok başkadır. Çift yarık deneyinden de hatırlayabileceğiniz üzere kuantum dünyasındaki bir parçacık aynı anda olası tüm yolları izler. İşte Feynman yol integralinin dayanak noktası burasıdır. Parçacık mümkün olan tüm yolları aynı anda aldığından bunu yol integraliyle hesaplayabiliriz.
Yol integrali kabaca her olası yolu saptar ve her bir yolun genliğini hesaplar. Çıkan sayı size parçacığın o yolu alma olasılığının ne kadar olduğunu söyler. Daha sonra tüm olası yolların genliklerini toplayarak Feynman yol integralini hesaplamış olursunuz. Dolambaçlı yollarda vektörler zıt yönlere baktığı için birbirlerini söndürür. Fakat düz yollarda vektörler aynı yöne baktığından birbirini güçlendirir. Bu sayede de tüm olası yollardan geriye bir tek klasik düz yol kalır.
Sonuç olarak
En az eylem ilkesi büyüleyici fikirdir. Yalnızca klasik mekaniğin değil, elektromanyetizmanın, genel göreliliğin, kuantum mekaniğinin ve sahip olduğumuz veya karşılaşacağımız her sistemin temel ilkelerini bize özetler. Bundan sonrasında yokuş aşağı yuvarlanan bir top gördüğünüz zaman onun düz gitmesinin nedeninin en az eylem ile ilgili olduğunu anımsayınız.
Kaynaklar ve ileri okumalar
- Wen, YL., Wang, Y., Tian, LM. et al. Demonstration of the quantum principle of least action with single photons. Nat. Photon. 17, 717–722 (2023). https://doi.org/10.1038/s41566-023-01212-1
- Wen, Yong-Li & Wang, Yunfei & Tian, Li-Man & Zhang, Shanchao & Li, Jianfeng & Du. Jing-Song & Yan, Hui & Zhu, Shi-Liang. (2023). Demonstration of the quantum principle of least action with single photons. Nature Photonics. 17. 1-6. 10.1038/s41566-023-01212-1.
- Principle of Least Action — an Introduction. Yayınlanma tarihi: 26 temmuz 2022. Bağlantı: Principle of Least Action — an Introduction
- Explaining the Principle of Least Action: Physics Mini Lesson; Bağlantı: https://www.youtube.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










