Uzun uğraşlar sonucu matematikçiler, dokuzuncu Dedekind sayısını bulmayı başardılar. Peki ama nedir bu Dedekind sayısı? Matematikçiler 42 basamaklı bir sayıyı bulmak için neden 32 yıl uğraştı?

1897 yılında Richard Dedekind, belirli bir sayısal örüntü üzerine yaptığı bir araştırmayı yayımladı. Bu çalışma, daha sonra Dedekind sayıları olarak adlandırılacak bir sayı dizisini tanımlamasına yol açtı. Bu sayılar, ilk bakışta ilgisiz birçok farklı matematiksel yapıyı saymak için kullanılıyordu. Dedekind makalesini şu gözlemle bitirmişti. “Bu gruplarda yer alan elemanların sayısı oldukça hızlı artıyor gibi görünüyor.”
Bu konuda kesinlikle haklıydı. Söz konusu çalışmasında ilk dört terimi hesapladıktan sonra devam etmekten vazgeçti. Dördüncü terim için bulduğu değer —166— hakkında bile emin değildi. (Bugün bu sayı genellikle 168 olarak kabul edilmektedir.)
Beşinci ve altıncı terimler 1940’larda, yedincisi ise 1965’te hesaplandı. 1991 yılında, Thinking Machines Corporation adlı süper bilgisayar şirketinde çalışan Doug Wiedemann, sekizinci Dedekind sayısı d(8)’i hesaplamak için 200 saatlik bir işlem yürüttü. Sonuç: 56.130.437.228.687.557.907.788. olacaktı. Gerçekten de çok hızlı bir artış.

Son olarak birbirinden habersiz iki ayrı araştırma grubu bağımsız yöntemlerle bu sayıyı hesaplayıp üç gün arayla duyurdu. Hesaplanan d(9) yani dokuzuncu Dedekind sayısı tam 42 basamaklıydı.
Julius Wilhelm Richard Dedekind Kimdir?
6 Ekim 1831’de Almanya’nın Braunschweig (Brunswick) kentinde doğan Dedekind, entelektüel bir ailenin en küçük çocuğuydu. Dedekind genç yaşta yerel bir Gymnasium’da eğitim gördü. Başlangıçta fiziğe ilgi duysa da, bu alanın “fazla dağınık” olduğunu düşünerek matematiğe yöneldi.
1850’de Göttingen Üniversitesi’ne girdi ve orada Bernhard Riemann ile dostluk kurdu. Carl Gauss, Moritz Stern ve Wilhelm Weber gibi dönemin önde gelen akademisyenlerinden ders aldı. Sadece iki yıl içinde, Euler integralleri üzerine yazdığı tezle, Gauss’un danışmanlığında doktorasını tamamladı.
Eğitimine Berlin’de devam eden Dedekind, burada Carl Jacobi ve Gustav Lejeune Dirichlet’in derslerine katıldı. 1854’te Berlin Üniversitesi’nde öğretim görevlisi olarak olasılık kuramı ve geometri dersleri vermeye başladı. Bu sırada Dirichlet ile yakın arkadaş oldu; bu dostluk, onun entelektüel çevresini önemli ölçüde genişletti.1862’de memleketi Braunschweig’e döndü ve yaşamının geri kalanını burada geçirdi.
Dedekind’in en önemli katkılarından biri, “Dedekind kesimi” olarak bilinen yöntemle gerçek sayıları tanımlamış olmasıdır. O dönemde matematikçiler, sayı kavramının özellikle irrasyonel (kök 2 gibi, kesirli olarak yazılamayan) sayılar söz konusu olduğunda net bir tanımını yapamıyordu. Dedekind bu boşluğu fark etti. Gerçek sayıları anlamak için düzen kavramına getirdiği yaklaşım, günümüzde de analizde temel referanslardan biri olarak kabul edilmektedir.
Dedekind Sayıları Nedir?
Dedekind sayıları, matematikte oldukça karmaşık ama ilginç yapıları saymak için kullanılır. Bu sayıların üç farklı ama eşdeğer tanımı vardır. Her tanım aynı sayıya ulaşır ama farklı bakış açıları sunar.
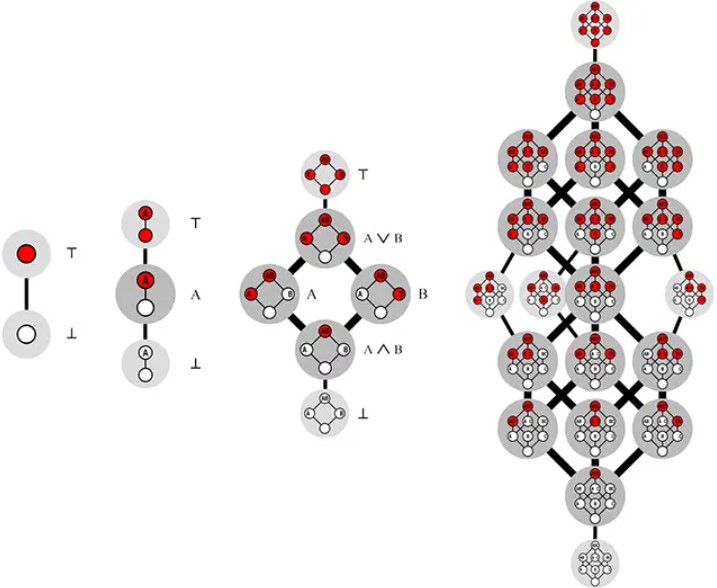
0, 1, 2 ve 3 boyutları için Dedekind sayılarını oluşturan kesimlerin gösterimi. Bu gösterimde doğru/yanlış ya da 1’ler ve 0’lar yok. Ancak mantık hala aynı. Kırmızı ve beyaz renkler doğru/yanlışları ya da 0-1’leri temsil ediyor.
Küpün köşelerini boyayarak tanım (geometrik yaklaşım):
Bir n-boyutlu küp düşünelim. Bu küpün köşeleri iki renkten biriyle, örneğin mavi veya beyaz olacak şekilde boyanacak. Kural şudur: hiçbir mavi köşe, beyaz bir köşeden daha yukarıda bulunmamalıdır. Bu koşula uyan kaç farklı renklendirme yapılabileceği sorusu, o boyuttaki Dedekind sayısını verir. Örneğin 2 boyutlu bir küp yani kare için bu kurala uyan 6 farklı renklendirme mümkündür. Bu nedenle d(2) = 6’dır.
Küme kuramına dayalı tanım:
Bu sefer n öğeli bir kümenin tüm altkümeleri alınır. Toplamda 2ⁿ adet altküme oluşur. Bu altkümelerden bir grup seçilir. Seçim kuralına göre, hiçbir altküme, başka bir altkümeyi içermemelidir. Bu şekilde oluşturulan gruplara antizincir denir ve tüm antizincirlerin sayısı yine d(n) olur.
Mantık yoluyla tanım (Boolean fonksiyonları):
Burada mantıksal bir sistem düşünülür. Sonucunda n tane 0–1 girişi olan bir Boolean fonksiyonu, her giriş kombinasyonu için 0 ya da 1 çıktısı üretir. Şimdi şöyle bir özellik koyalım: Girişlerdeki 0’ları birer birer 1’e çevirirken çıktı bir kez 1 olduysa bir daha asla 0’a dönmesin. Bu tür fonksiyonlara monoton Boolean fonksiyonları denir. Kaç tane böyle fonksiyon olduğunu sorarsan, cevabı yine Dedekind sayısı olacaktır.
Dedekind sayıları hızla büyür. Örneğin d(1) = 2, d(2) = 6, d(3) = 20 şeklinde artar ve d(9) sayısı ise 42 basamaklıdır. Bu sayı öyle büyüktür ki, doğrudan brute-force (deneme-yanılma) hesaplamayla bulunması mümkün değildir. Hatta gerekli belleği Dünya’daki tüm bilgisayarlar toplansa bile karşılayamaz.
Bu kadar karmaşık bir yapının üç farklı ama eşdeğer tanımı olması, matematiğin soyut gücünü ve yapıların farklı dillerle nasıl tanımlanabildiğini gösteren çarpıcı bir örnektir.
Sonuç olarak
Dedekind sayılarının hesaplanması, içerdiği devasa sayıların büyüklüğü nedeniyle tarih boyunca teknolojik ilerlemeyle yakından bağlantılı olmuştur. Bilgisayar bilimci Patrick De Causmaecker, bu hesaplamaları yalnızca matematiksel bir çalışma olarak değil, aynı zamanda “güncel bilgisayar teknolojisinin bir testi” olarak tanımlar.
20. yüzyıl boyunca yeni Dedekind sayıları zaman zaman hesaplanmış, ancak her birinin bulunması için genellikle onlarca yıl beklenmiştir. Bu da hesaplamanın yalnızca kuramsal bilgiyle değil, aynı zamanda ileri düzey bilgisayar gücüyle de mümkün olduğunu göstermektedir. 10. Dedekind sayısının bulunması büyük olasılıkla uzun bir zaman alacak, çünkü bu sayı, D(9)’dan katbekat daha büyük olacak.
Kaynaklar ve İleri Okumalar
- Mathematicians Discover The Ninth Dedekind Number, After 32 Years of Searching. Bağlantı: Mathematicians Discover The Ninth Dedekind Number, After 32 Years of Searching : ScienceAlert. Yayınlanma tarihi: 28 Haziran 2023
- Ninth Dedekind Number Discovered Using Supercomputer. Solving the Long-Standing Problem That Has Mystified Mathematicians for 32 Years. Bağlantı: Ninth Dedekind Number Discovered Using Supercomputer, Solving the Long-Standing Problem That Has Mystified Mathematicians for 32 Years | Science Times. Yayınlanma tarihi: 30 Haziran 2023
- Ninth Dedekind number discovered: Scientists solve long-known problem in mathematics. Bağlantı: Ninth Dedekind number discovered: Scientists solve long-known problem in mathematics (phys.org). Yayınlanma tarihi: 26 Haziran 2023
- Jäkel, Christian. (2023). A computation of the ninth Dedekind Number A Preprint. 10.48550/arXiv.2304.00895.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





