Antik uygarlıkların bilgi birikimi, yalnızca kendi dönemlerindeki sorunlara çözüm getirmekle kalmadı; modern dünyanın temellerini de attı. Bugün kullandığımız pek çok matematiksel kavram ve formül, antik uygarlıkların olağanüstü zekâsı ve yaratıcılığı sayesinde doğdu.

Einstein’ın ünlü denklemleri ya da Newton’un hareket yasaları bilim tarihinde nasıl bir dönüm noktası olduysa, antik matematikçilerin geliştirdiği yöntemler de kendi çağları için birer devrim niteliğindeydi.
Kesik Piramidin Hacmi
Antik Mısır piramitleri, yalnızca mimari harikalar değil; aynı zamanda matematiksel zekânın da en etkileyici örneklerindendir. Yaklaşık 4.600 yıl önce inşa edilen Giza Piramidi, Mısırlıların ileri düzey matematik bilgisine sahip olduğunu açıkça gösterir. Bu uygarlık, piramitlerin hacmini hesaplamak için basit ama son derece etkili bir formül geliştirmiş ve inşaatlarında ustalıkla kullanmıştır.
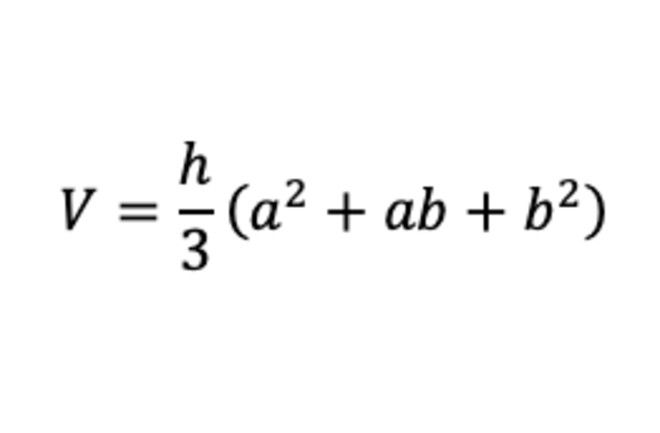
Mısırlılar, piramidin taban alanı ve yüksekliğini esas alan bir yöntemle hacmi hesaplıyorlardı. Bu formül, ilk bakışta sade görünse de oldukça güçlüydü. Doğruluğunu sınamak için piramit ve prizma modelleri üzerinde deneyler yaptılar. Aynı taban alanına ve yüksekliğe sahip bir prizmanın, piramidin hacminin tam üç katı olduğunu fark ettiler. Bu yöntem, dönemin matematiksel düşünce seviyesinin ne kadar ileri olduğunu ortaya koyar.
Daha zorlu bir mesele ise kesik piramitlerin (frustum) hacmini hesaplamaktı. Üst kısmı eksik bu yapılarda, hem alt hem de üst taban alanlarının hesaba katılması gerekiyordu. Antik Mısırlılar bu sorunu çözmek için, günümüze ulaşan Moskova Papirüsü’nde (M.Ö. 1850 civarı) bir formül geliştirdiler.

Bu başarı, tarihçiler tarafından “antik geometrinin bir şaheseri” olarak nitelendirilmektedir. Tarihçi David Burton, Mısırlıların bu formülü yalnızca matematiksel bir zafer olarak değil, aynı zamanda piramitlerin inşasında gerekli malzeme miktarını hesaplamada son derece pratik bir araç olarak kullandıklarını vurgulamıştır.
Pisagor Teoremi
Geometride herkesin hatırladığı en temel kavramlardan biri, büyük olasılıkla Pisagor Teoremidir. Bu teorem, bir dik üçgende hipotenüsün karesinin, diğer iki kenarın karelerinin toplamına eşit olduğunu ifade eder. Ancak kökenlerinin yalnızca Pisagor’a değil, Yunanistan’dan çok daha eski uygarlıklara dayandığını öğrenmek şaşırtıcıdır.
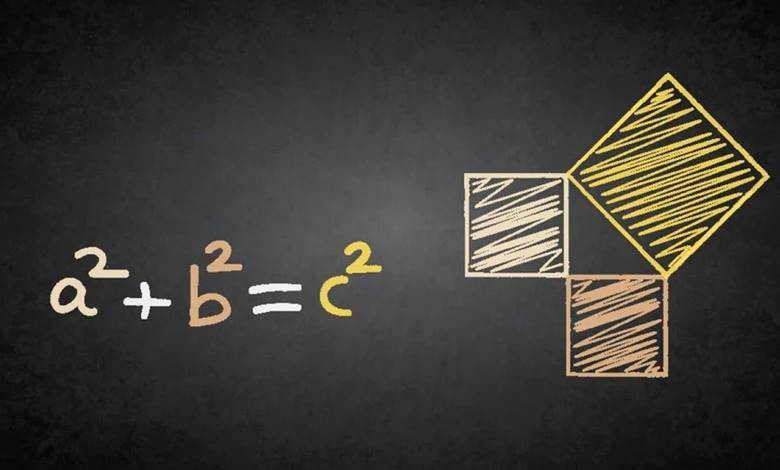
Antik Babil, Pisagor Teoremi’nin ilk izlerini taşıyan uygarlıklardan biridir. M.Ö. 1800’lere tarihlenen Plimpton 322 tableti, bu teoremin hem pratik uygulamalarını hem de teorik temellerini ortaya koyar. Tablet, Pisagor üçlüleri adı verilen ve teoremi sağlayan tam sayı gruplarını içerir. Babil matematikçileri, bu üçlüleri yalnızca soyut bir teori olarak değil, aynı zamanda arazi ölçümünde etkili bir yöntem olarak kullanmıştır.
Modern araştırmalar, Plimpton 322’deki bilgilerin Mezopotamyalı arazi ölçümcüler tarafından doğru açılar oluşturmak ve alan hesaplamak için kullanıldığını göstermektedir. Antik dünyada Pisagor Teoremi yalnızca matematiğin gelişimini etkilemekle kalmamış; tarım arazilerinin sınırlarını belirleme, binaların temel geometrisini hesaplama ve sulama sistemlerini düzenleme gibi pek çok alanda da pratik çözümler sunmuştu
İkinci Derece Denklemler
Babil matematikçileri, ikinci dereceden denklemleri çözmede son derece başarılıydı. Modern öğrenciler bu denklemleri genellikle soyut ve karmaşık bulurken, Babilliler onları çok daha somut terimlerle ele almışlardı.
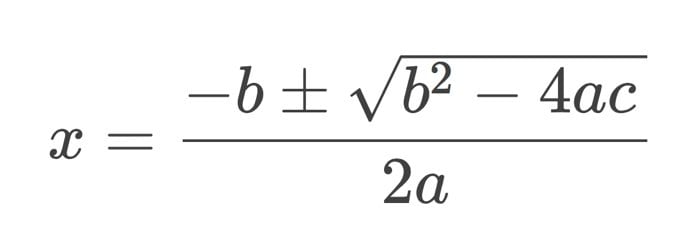
Harflerle çalışmak yerine problemleri “uzunluk,” “genişlik” ve “alan” gibi somut kavramlarla ifade ettiler. Bu pratik yaklaşım, hem günlük yaşamın ihtiyaçlarına çözüm sağladı hem de sayılar arasındaki soyut ilişkilerin daha iyi anlaşılmasına imkân verdi.
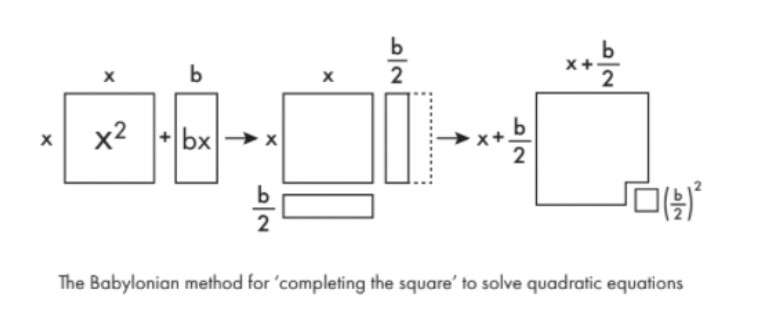
Babil matematikçilerinin ikinci dereceden denklemleri çözme yöntemleri, bugün kullandığımız cebirsel formüllerin temelini oluşturan önemli bir mirastır. Bu yaklaşımlar, tarımdan inşaata kadar pek çok pratik alanda uygulanmış, aynı zamanda matematiğin soyut yönlerinin keşfedilmesine de kapı aralamıştır.
Thales Teoremi
Geometri denildiğinde antik Yunanlılar özel bir yere sahiptir. Bu bağlamda Thales Teoremi, matematik tarihinde önemli bir dönüm noktasıdır. Teoreme göre, bir çemberin çapı üzerine kurulan üçgenin açılarından biri daima diktir.
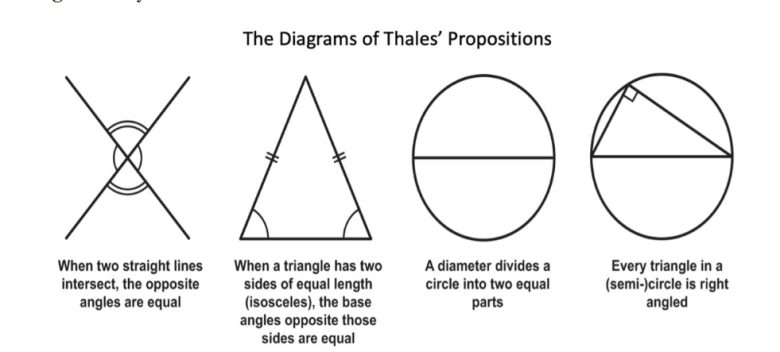
Bu teorem bugün bize basit görünecektir. Ancak M.Ö. 6. yüzyılda Thales ve çağdaşları, matematiği adeta sıfırdan inşa ediyorlardı. Babil’de edindiği fikirleri geliştiren Thales, bu teoremi mantıksal bir ispatla sunarak matematiği soyut bir uğraştan çıkarıp kanıtlanabilir bir bilim haline getirdi.
Bu yaklaşımıyla Thales, “ilk gerçek matematikçi” unvanını hak eder. Onun çalışmaları, geometrinin yalnızca pratik bir araç olmasının ötesine geçmesini sağladı ve disiplini sistematik bir mantık temeline oturttu.
Arşimet’in Sığır Problemi
Antik dünyanın en büyük matematikçilerinden biri olan Arşimet, geometri ve mekanikte devrimler yaratırken, aynı zamanda matematiğin eğlenceli ve yaratıcı yönlerini keşfetmesiyle de tanınır. Bu özelliklerinin en çarpıcı örneklerinden biri, onun ünlü Sığır Problemidir.
Arşimet bu problemi, Homeros’un Odysseia adlı eserindeki şu dizeden esinlenerek tasarladı. “Güneşin çok sayıda öküz ve koyunu beslediği Thrinacia Adası’na ulaşacaksınız.” Bu mitolojik sahne, Arşimet’e bir matematiksel bulmaca oluşturma fikrini verdi.
Sığır Problemi, bugün “Pell Denklemi” olarak bilinen özel bir ikinci derece denkleme dayanıyordu. Ancak Arşimet’in dönemindeki yöntemler, bu tür denklemleri tam olarak çözmeye yetmiyordu. Denklemi formüle etmek mümkündü, fakat kesin çözüme ulaşmak imkânsızdı. Bu nedenle problem, yüzyıllar boyunca matematikçiler için bir meydan okuma olarak kaldı.
Nihayet 1965’te, modern bilgisayar teknolojisinin yardımıyla çözüm bulundu. Ortaya çıkan sayı tam 206.545 basamaklıydı. Bu olağanüstü büyüklükteki çözüm, matematik tarihinde önemli bir dönüm noktası olarak kabul edilmektedir.
Antik Matematiğin Mirası
Antik matematikçiler, yalnızca inşaat, ölçüm veya ticaret gibi pratik ihtiyaçları karşılamakla kalmadılar. Aynı zamanda evrenin derinliklerini anlamak ve soyut düşüncenin sınırlarını keşfetmek için de çalıştılar. Bugün modern dünyada kullandığımız pek çok matematiksel yöntem ve kavram, onların attığı temeller üzerine kuruldu.
Antik Mısırlıların geometri bilgisi, Babillilerin cebirsel zekası ve Yunanlıların mantıksal ispat yöntemleri, modern bilim ve teknolojinin yapı taşlarını oluşturdu. Onların mirası, bugün bile bilimin ve teknolojinin ilerlemesine ışık tutmaya devam ediyor.
Kaynaklar ve ileri okumalar
- 5 Mathematical Formulas from Ancient Times. Kaynak site: Dşscover Magazine. Yayınlanma tarihi: 3 Aralık 2024. Bağlantı: 5 Mathematical Formulas from Ancient Times
- Lenstra, Hendrik. (2002). Solving the Pell Equation. Notices Amer. Math. Soc.. 49.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






