Birçok kişiye ünlü bir matematikçi adı sorulduğunda, akla gelen ilk isim çoğu zaman Pisagor olur. Bugün hâlâ bu denli tanınmasının temel nedeni, adını taşıyan ünlü teoremdir. Pisagor teoremi iki bin yılı aşkın bir süredir öğretilir ve zamanla popüler kültürün de bir parçası hâline gelmiştir.

Yunanlar, Pisagor teoremini modern anlamda sembolik bir denklem olarak ifade etmiyordu. Bu tür bir gösterim, cebirin gelişmesiyle birlikte çok daha sonra ortaya çıktı. Teoremin ilk yazılı ispatına ise İskenderiyeli Öklid’in eserlerinde yer verdi.
Teorem, Elementler’in birinci kitabında 47. önerme olarak yer alır. “Dik açılı üçgenlerde, dik açının karşısındaki kenar üzerine kurulan karenin alanı, dik açıyı oluşturan kenarlar üzerine kurulan karelerin alanlarına eşittir.”
Yunanlar, ileri matematikte sayılar yerine doğru parçaları ve alanları kullanıyordu. Bu nedenle Pisagor ve onu izleyen Yunan matematikçileri teoremi bir alan eşitliği olarak yorumladı. Onlara göre bir dik üçgenin en uzun kenarı üzerine kurulan karenin alanı, diğer iki kenar üzerine kurulan karelerin alanları toplamına eşitti. En uzun kenar, bugün hipotenüs adını verdiğimiz kenardır.
Yaklaşık iki bin yıl içinde Pisagor teoremi, günümüzde kullanılan cebirsel denklem biçimine dönüştürüldü: a² + b² = c². Bu ifadede c hipotenüsün uzunluğunu, a ve b diğer iki kenarın uzunluklarını gösterir.
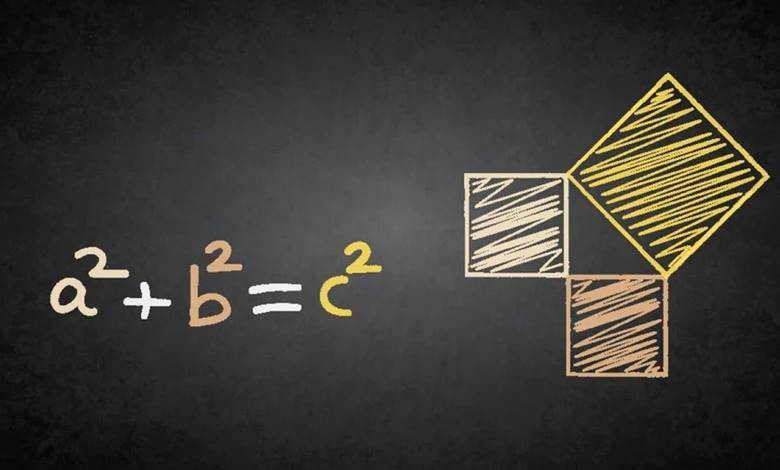
Pisagor Teoremini Kim Buldu?
Pisagor teoreminin, Pisagor’dan çok daha önce bilindiğini düşündüren kanıtlar vardır. British Museum’da bulunan bir Babil kil tabletinde, bir matematik problemi ve çözümü yer alır. Metin, bugünkü dile aktarıldığında şu anlama gelir: Bir kenarın uzunluğu 4, köşegenin uzunluğu 5’tir. Genişlik nedir? Bu soru, Babillilerin 3–4–5 üçgenini Pisagor’dan bin yıl önce bildiklerini ortaya koyar.

Yale Üniversitesi’nin Babil koleksiyonunda yer alan YBC 7289 numaralı tablet de, kenar uzunluğu 30 olan bir karenin çizimi ve köşegeni için verilen sayılar yer alır. Babillilerin kullandığı 60 tabanlı sayı sistemiyle yazılmış bu değerler, karekök 2’nin yaklaşık 1,4142129 olarak hesaplandığını ortaya koyar.
Gerçek değerin 1,4142135 olduğu düşünülürse, ulaşılan doğruluk dikkat çekicidir. Aynı tablet, köşegen uzunluğunun bu değerin 30 ile çarpımı olarak alındığını da gösterir. Bütün bunlar, Babillilerin bir karenin köşegeninin, kenar uzunluğunun karekök 2 ile çarpımına eşit olduğunu bildiklerini açıkça ortaya koyar.
Ayrıca Plimpton 322 adlı Babil tableti, bir sayı tablosudur. Her satırda, üçüncü sütundaki sayının karesinden ikinci sütundaki sayının karesi çıkarıldığında, sonuç yine bir tam karenin karesi olur. Bu düzen, a² + b² = c² bağıntısına karşılık gelir ve tabletin Pisagor üçlülerini içerdiğini düşündürür.
Pisagor’un gençliğinde Mısır’ı ziyaret etmiş olabileceğine ve teoremi orada öğrenmiş olabileceğine dair bazı varsayımlar vardır. Ancak günümüze ulaşan Mısır matematiği belgeleri bu düşünceyi güçlü biçimde desteklemez.
Pisagor Teoremi Ne İşe Yarar?
Günlük hayatta karşılaşılan üçgenlerin çoğu dik açılı değildir. Ancak her üçgen iki dik üçgene ayrılabilir ve her çokgen de üçgenlere bölünebilir. Bu nedenle dik üçgenler, üçgenin biçimi ile kenar uzunlukları arasındaki ilişkiyi ortaya koyan temel yapılardır. Bu ilişkiden doğan matematik dalı trigonometridir. Trigonometride dik üçgen ve beraberinde de Pisagor teoremi merkezî bir konuma sahiptir.
Trigonometri denklemleri ve uygun ölçüm araçlarıyla donanmış olduğumuzda, arazi ölçümleri yapmak ve doğru haritalar üretmek mümkün olur. Pisagor teoremi, koordinat geometrisinin ortaya çıkmasında da temel bir rol oynamıştır ve bize iki temel sonuca götürür. Hangi denklemlerin çemberleri tanımladığını gösterir ve koordinatlarla verilen noktalar arasındaki uzaklığın nasıl hesaplanacağını açıklar.
Sonuç olarak
Pisagor denklemi, yaklaşık 3.500 yıl önce bir çiftçinin tarlasını ölçme ihtiyacından doğdu. Dik açılı olmayan üçgenlere ve küre üzerindeki üçgenlere genelleştirilmesi, kıtaların haritalanmasını ve gezegenimizin ölçülmesini mümkün kıldı. Küçük ve pratik bir ihtiyaçla başlayan bu fikir, insanlığın uzayı kavrayışını şekillendiren temel araçlardan birine dönüştü
Kaynaklar ve ileri okumalar için:
- Britannica, The Editors of Encyclopaedia. “Pythagorean theorem”. Encyclopedia Britannica, 10 May. 2024, https://www.britannica.com/science/Pythagorean-theorem. Accessed 22 May 2024.
- High school students who came up with ‘impossible’ proof of. Pythagorean theorem discover 9 more solutions to the problem. Yayınlanma tarihi: 28 Ekim 2024. Kaynak site: Live Science. Bağlantı: High school students who came up with ‘impossible’ proof of. Pythagorean theorem discover 9 more solutions to the problem
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





