Metre, cetvel ya da şerit ölçü kullandığımızda, ölçmeye çalıştığımız nesnenin gerçekten ölçülebilir olup olmadığını hiç sorgulamayız. Matematikçiler de 19. yüzyılın sonlarına kadar böyle sanıyordu. Ancak sonrasında da ölçüm problemi ile yüzleşmek zorunda kalacaklardı.

İntegraller ve türevler, geometrik şekillerin büyüklüğünü hassas biçimde hesaplamayı mümkün kıldı. Buna rağmen iki yüzyıldan fazla bir süre boyunca kimse, “bir nesnenin ölçülebilir olması tam olarak ne demektir?” sorusunu ciddi biçimde sormadı.
Bu sorgulama 19. yüzyılın sonlarına doğru başladı. Matematiği sağlam temellere oturtmak isteyenler, kümeler kuramını merkeze aldı. Bu yaklaşıma göre, tüm matematiksel yapılar — şekillerden denklemlere kadar — en temel kümelere indirgenebilirdi. Ancak eğer şekiller sadece kümelerden ibaretse, o zaman bu kümeleri nasıl ölçeceğimizi de açıkça tanımlamamız gerekiyordu.
Sayı doğrusunda [0, 1] aralığını düşünün. Bu aralık sonsuz sayıda reel sayı içerir, ancak uzunluğunu bir santimetreye eşit kabul edelim. Matematikçiler birimleri kullanmadan hesap yapmayı tercih ettikleri için bu aralığın uzunluğunu 1 olarak tanımlarlar. Aynı şekilde, [0, 2] aralığının uzunluğu 2, [0, a] aralığının uzunluğu ise a olur. Bu düşünce, ölçme kavramının kümeler kuramı içinde nasıl genelleştirileceğine dair ilk adımı oluşturur.
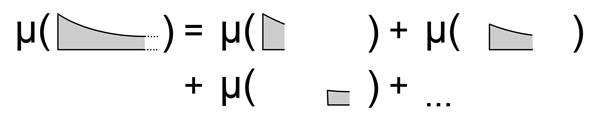
Elbette bu sonuçlar keyfi biçimde belirlenmedi. Matematikçiler belirli kurallardan yola çıkarak bunları türetti. Amaç, uzunluk, alan ya da hacim gibi ölçülerin sahip olması gereken sezgisel özellikleri sistemli bir biçimde tanımlamaktı.
Bu özellikler üç temel ilkeye dayanır. Boş kümenin ölçüsü sıfır olmalıdır; bir nesne taşındığında veya döndürüldüğünde ölçüsü değişmemelidir; ve birbiriyle kesişmeyen nesnelerin toplam ölçüsü, her birinin ölçülerinin toplamına eşit olmalıdır. Bu üç basit ilke, farklı boyutlarda ölçü kavramını tanımlamayı mümkün kılar.
Bu yöntem ilk bakışta gereksiz derecede ayrıntılı görünecektir. Sonuç zaten sezgisel gibi durur. Ancak bu yaklaşımın asıl gücü, ölçme kavramını yalnızca geometrik şekillerle sınırlamamasıdır. Bu sayede, doğrudan görsel bir karşılığı olmayan, soyut nicelikler için de tutarlı biçimde ölçüm yapmak mümkün olur.
Soyut Nicelikler İçin Ölçü
Matematikçiler ölçü kavramını incelemeye başladıklarında, öncelikle fonksiyonlara yöneldiler. Fonksiyon, iki değişken arasındaki ilişkiyi tanımlayan bir ifade ya da kuraldır. Bir fonksiyonun altındaki alan integralle hesaplanır.
Eğrinin altındaki alanı hesaplamak için x ekseni küçük aralıklara bölünür. Ardından bu aralıkların oluşturduğu üst ve alt toplamlar alınır. Böylece her aralığa karşılık gelen küçük dikdörtgenlerin alanları toplanarak, eğrinin altındaki toplam alanın yaklaşık değeri bulunur.
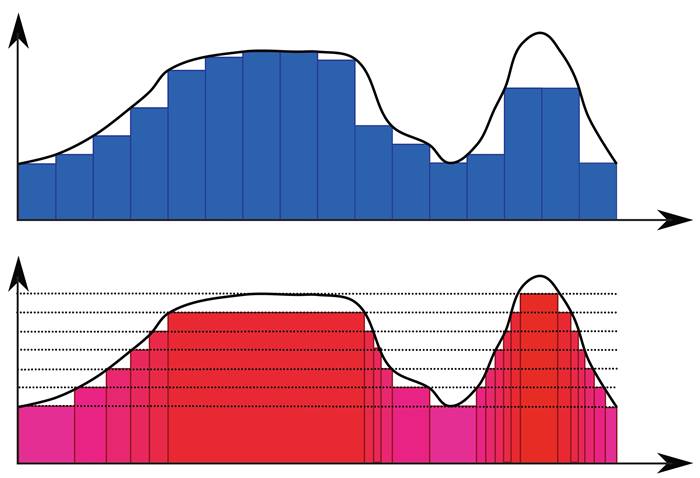
Ancak kimi fonksiyonlar bazen son derece karmaşık olur. Grafiği çizmeye çalıştığınızda, kopuk noktalar mevcut olduğunu görürsünüz. Bu noktalar arasında hiçbir süreklilik bulunmadığından, klasik Riemann integraliyle bu tip fonksiyonun altında bir alan tanımlamak mümkün değildir.
Bunun yerine 1902’de Henri Lebesgue tarafından geliştirilen Lebesgue integrali kullanılır. Bu yaklaşımda, bölme işlemi x ekseni yerine y ekseninde gerçekleşir.. Yani önce y ekseni küçük aralıklara ayrılır. Ardından her y değeri için x ekseninde bu değere karşılık gelen aralıkların genişliği hesaplanır. Sıradan, düzgün fonksiyonlarda her iki yöntem aynı sonucu verir. Ama Lebesgue integrali, parçalı, karmaşık ve “dağınık” fonksiyonlar için de çalışır.
1902’de Lebesgue integrali ortaya atıldığında, matematikte önemli bir soru gündeme geldi: Her kümeye ölçü atamak mümkün mü? Bu sorunun yanıtı yalnızca üç yıl sonra, 1905’te İtalyan matematikçi Giuseppe Vitali’den geldi. Ve cevabı oldukça çarpıcıydı: Hayır.
Ölçüm Problemi Ortaya Çıkıyor
Bazı kümeler o kadar karmaşıktır ki, hiçbir ölçüm yöntemiyle onlara anlamlı bir ölçü atamak mümkün değildir. Vitali bu sonuca teorik bir çıkarımla değil, doğrudan ölçülemeyen somut bir örnek oluşturarak ulaştı. Bugün bu kümeye onun adıyla, Vitali Kümesi denir.
İşe 0 ile 1 arasındaki sayı aralığını inceleyerek başladı. Bu aralık içindeki sayıları, farkları rasyonel sayı olanlar aynı gruba düşecek şekilde sınıflandırdı. Yani, eğer a−b bir rasyonel sayıysa, a ve b aynı sınıfa aittir.
Örneğin tüm doğal sayılar ve genel olarak tüm rasyonel sayılar bu tanıma göre aynı kümeye düşer. Başka bir alt kümede ise irrasyonel farklara sahip sayılar olur. Bu yöntemle Vitali, [0, 1] aralığını sonsuz sayıda küçük parçaya ayırmış oldu.
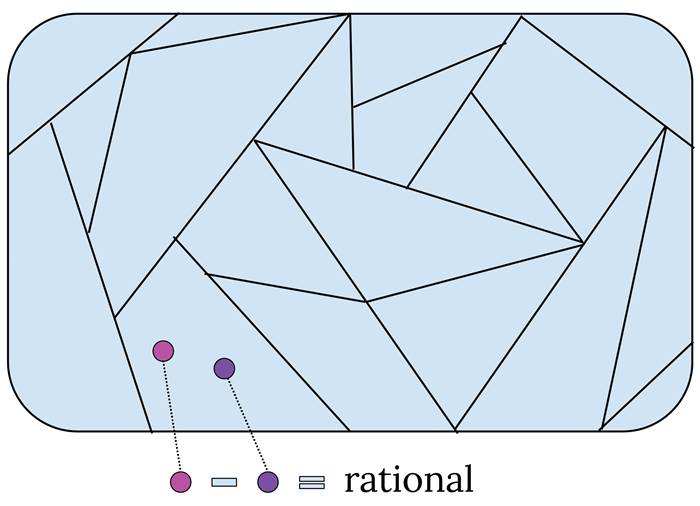
Sonraki adımda Vitali, oluşturduğu her gruptan yalnızca bir tane sayı seçti ve yeni bir küme içinde topladı. Bu kümeye V kümesi adını verdi. Ardından V kümesini, –1 ile 1 arasındaki bir rasyonel sayı p kadar kaydırdı ve bu yeni kümeyi Vp = V + p olarak tanımladı. Bu durumda
- Eğer p = –1 olursa, V kümesi 1 birim sola kayar ve yaklaşık [–1, 0] arasına gelir.
- Eğer p = 1 olursa, 1 birim sağa kayar ve yaklaşık [1, 2] arasına gelir.
Bu kümelerin hepsini birleştirince ortaya V* adlı yeni bir küme çıktı. Bu küme [–1, 2] aralığında kalıyor, yani uzunluğu en fazla 3 birim olmalıdır. Aynı zamanda [0, 1] aralığını da kapsadığı için en az 1 birim uzunluğundadır. Bu yüzden ölçüsü 1 ile 3 arasında bir yerde olur.

Ancak bu aralıkta bir değer seçmek mümkün değildir çünkü bu kümenin ölçüsünü tanımlamak için gereken mantıksal koşullar birbiriyle çelişir. Başka bir deyişle, Vitali kümesi ölçülemez. Yani, bir kümenin belirli bir aralıkta bulunması, onun ölçülebilir olduğu anlamına gelmez.
Sonuç olarak
Vitali kümesi sınırlıdır ve yalnızca reel sayılardan oluşur, ama aynı fikir iki boyuta taşındığında işler garipleşir. Bir küreyi ölçülemez alt kümelere ayırarak yüzey alanını iki katına çıkarmak, matematiksel olarak mümkündür.
Yine de ölçülemez kümeler son derece ender görülür. Fizikte bunlara rastlanmaz, çünkü nesneleri atom ölçeğinin ötesinde parçalayamayız. Bu tür kümeler yalnızca soyut olarak, özel biçimde inşa edilebilir. Fakat sayı doğrusunun en basit aralıklarında bile ölçülemez parçalar gizlidir.
Onlardan tamamen kurtulmak da kolay değildir. Bunun için, matematiğin temelini oluşturan aksiyomları değiştirmek gerekir.
Kaynaklar ve ileri okumalar
- Solovay, Robert. (1970). A Model of Set Theory in Which Every Set of Reals is Lebesgue Measurable. Annals of Mathematics. Second Series. 92. 10.2307/1970696.
- Mathematicians Explain Why Some Lengths Can’t Be Measured. Kaynak site: Scientific Americaç Yayınlanma tarihi: 18 Nisan 2024. Bağlantı: Mathematicians Explain Why Some Lengths Can’t Be Measured.
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





