Düğümlenen kulaklıklar canınızı sıkıyorsa, aslında bunun bir nedeni var. Bundan sonra, düğüm olan kulaklığınızı çözmeye çalışırken bunun sizin hatanız olduğunu düşünmeyin. İşin arka planında sessiz sedasız işleyen fizik ve matematik kanunlarının iş başında olduğunu anımsayınız.

Müzik dinlemek için çantamıza düzgünce yerleştirdiğimiz kulaklıklarımıza ihtiyaç duyduğumuz zaman genelde sinir bozucu bir durumla karşılaşırız. Kulaklıklarımız büyük bir ihtimal ile çantamızda düğümlenmiştir. Kulaklıklarınızı kot pantolonunuzun cebine koymayı aklınıza bile getirmeyin. Sorun daha da karmaşık hale gelecektir. Aslına bakarsanız, çoğu insan bir Rubik küpünü kulaklıklarından daha hızlı çözer.
Aslında bu durum sadece kulaklıklar için geçerli değildir. Aynı sorun kutuya koyduğumuz kolyelerimizde ya da herhangi bir başka şeyde de karşımıza çıkar. Hiç kimse bir kulaklığın kendi başına nasıl karıştığını gerçekten bilmiyor. Ancak bazı bilim insanları bu gizemli durumun düğüm teorisi ile ilgili olduğuna inanıyor. Yani birçoğumuzun anlam veremediği bu durumun aslında matematiksel bir açıklaması mevcuttur.
Düğüm Teorisi İle Düğümlenen Kulaklıkların Ne İlgisi Var?
Düğüm teorisi 1800’lerde, kulaklık icat edilmeden çok önce geliştirildi. O zamandan beri de bilim insanları kablolar, ayakkabı bağları, teller vb. birbirine karışma ihtimali olan bir çok durumu bu teori aracılığı ile açıklıyorlar.

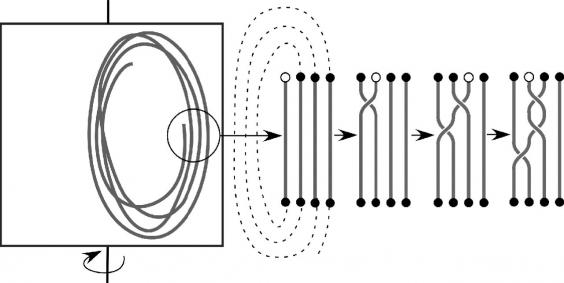
Düğümlenen kulaklıklar da 2007 yılında bilim insanlarının ilgisini çekecekti. Sonuçlar California Üniversitesinden iki fizikçi, Dorian M.Raymer ve Douglas E.Smith tarafından “Spontaneous knotting of an agitated string” başlıklı makalede kaleme alındı. Araştırmaları sırasında ekip bir motora bağlı dönen bir kutu içinde on saniye boyunca çeşitli uzunluklarda ip parçalarını yuvarladı.
Bu deneyi, farklı uzunluktaki teller, farklı boyutlarda kutular ve değişen dönme hızları ile kabaca 3.000 kez gerçekleştirdiler. Ortaya çıkan düğümleri matematiksel düğüm teorisini kullanarak analiz ettiler. Bu esnada, her bir türe karşılık gelen matematiksel denklemi bulmaya çalıştılar.
Çalışma sonucunda zamanın neredeyse %50’sinde ipin kendi kendine bir düğüm oluşturduğunu buldular. Anlaşılan bu düğüme iki şey neden oluyordu. Bunlar ”İpin uzunluğu” ve ”Sallanma miktarı” idi.
Kulaklıklar Ne Zaman Düğümlenecektir?
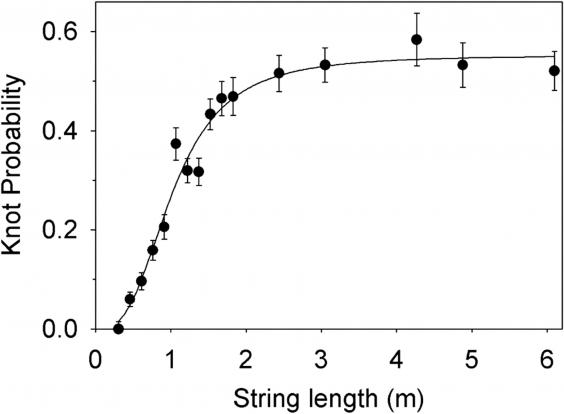
Tabloda da görebildiğiniz gibi, kablonun uzunluğu arttıkça ve daha uzun süre sallandıkça dolaşma olasılığı artıyor. Kablonun sertliği ve kalınlığı gibi biçimsel özellikler de önemli faktörler gibi gözükse de, aslında bunların sonuca bir bir katkıları yok.
Raymer ve Smith’in elde ettikleri bulgulara göre uzunluğu 46 santimetreden daha kısa olan bir kablo neredeyse hiçbir zaman kendi kendine düğümlenmiyor. 46 santimetre ile 150 santimetre arasında, bir düğümlenmenin oluşma olasılığı çarpıcı şekilde artıyor. Bundan daha uzun bir kabloda ise düğümlenmenin oluşma olasılığı yüzde 50’ye varıyor, sonrasındaysa artış yavaşlıyor.
Ayrıca kulaklarımızın şeklinin Y biçimde olması dolaşma ihtimalini arttıran etkenlerden. Tipik bir kulaklığın uzunluğu yaklaşık 120 cm-160 cm’dir. Bu nedenle kulaklığınızı çantanıza her koyduğunuzda düğümlenme olasılığı neredeyse yüzde elli kadardır. Kısacası bilim insanları, kulaklığınızı cebinize koyduğunuzda karışmaması için yapabileceğiniz hiçbir şey olmadığını söylüyorlar.
Kaynaklar ve ileri okumalar:
- Why do your earphones get tangled in your pocket? Science has the answer; Yayınlanma tarihi: 19 Temmuz 2014; Bağlantı: http://www.independent.co.uk
- Raymer DM, Smith DE. Spontaneous knotting of an agitated string. Proc Natl Acad Sci U S A. 2007 Oct 16;104(42):16432-7. doi: 10.1073/pnas.0611320104. Epub 2007 Oct 2. PMID: 17911269; PMCID: PMC2034230.
- How Does an Earphone Get Tangled Up All By Itself? Yayınlanma tarihi: 8 Temmuz 2022; Bağlantı: https://www.scienceabc.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel