Örgü örmek basit gibi görünür, ama arkasında oldukça karmaşık bir yapı vardır. Antik Mısır’dan kalma yün çoraplar, bu pratiğin en azından milattan sonra 3. yüzyıla dayandığını gösteriyor. Yine de bu kadar köklü bir geçmişe rağmen, örmenin fiziksel temelleri uzun süre anlaşılmadı.

Bugün bile gelişmiş dijital araçlar ve otomatik makineler devrede olsa da, belli bir ilmek deseninin kumaşta nasıl bir şekil alacağını önceden tahmin etmek hâlâ zor. Bilgi birikimi büyük ölçüde sezgiye ve deneme-yanılmaya dayanıyor.
Örgünün ardındaki fiziksel süreci anlamaya çalışan bazı araştırmacılar, bu zanaatı bilimsel bir yaklaşımla ele aldı. İlmeklere matematiksel bir tanım getirerek, örme işlemine fiziksel kurallar ve denklemlerle yaklaşmayı başardılar.
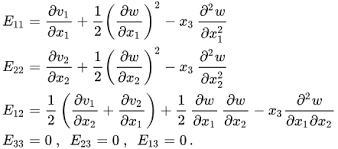
Geliştirdikleri model, düz ve ters ilmeklerin kumaşta yarattığı gerilimi Föppl–von Kármán denklemleriyle açıklıyor. Bu denklemler, ince ve esnek malzemelerin iç ve dış kuvvetler altındaki davranışını tanımlamak için kullanılıyor. İlmekleri bu şekilde haritalamak, kumaşı örmeden önce sanal ortamda test etmeye olanak tanıyor. Böylece kumaşın nasıl katlanacağı, hangi şekli alacağı ya da nasıl tepki vereceği önceden tahmin edilebiliyor.
Örgü Örmek İle Fizik Arasındaki İlişki Nedir?

Örmenin yapısını çözmeye çalışan bu çalışmada araştırmacılar, ilhamı beklenmedik bir yerden aldı: uzay-zamanın bükülmesini açıklayan genel görelilik kuramından. Bu kuram, kütleçekimin uzayı nasıl eğip büktüğünü açıklar. Araştırmacılar da benzer geometrik ilkeleri ipliğin ilmekler halinde dolanarak kumaşta nasıl kıvrımlar oluşturduğunu açıklamak için kullandı.
Hareket noktaları oldukça basitti. Örme kumaşlar belirli yönlerde kıvrılır. Örneğin bir tişörtün kollarını keserseniz, kumaş yukarı kıvrılacaktır. Bu genellikle sadece düz ilmekle örülmüş kumaşlarda olur.. Ters ilmekler ise kıvrımı ters yöne çeker. Düz ve ters ilmekler bir arada kullanıldığında işler değişir. Bu birleşim, kendi kendine katlanabilen karmaşık yapılar oluşturur.
Bu yaklaşımla, örme kumaş sadece birbirine geçmiş ilmeklerin oluşturduğu bir yapı olarak değil, ilmek diziliminin belirlediği içsel eğriliğe sahip sürekli bir yüzey olarak değerlendirildi. Araştırmacılar, malzemelerin nasıl bükülüp gerildiğini açıklayan elastisite kuramını kullanarak bir model geliştirdi. Bu model, iplik üzerindeki kuvvetleri simüle ediyor ve kumaşın uzayda nasıl şekil değiştireceğini öngörüyor.

Yapılan simülasyonlar, kumaşın mekanik özelliklerinin çoğu zaman malzemenin türünden çok ilmek geometrisine bağlı olduğunu gösterdi. Yün, pamuk ya da sentetik iplik kullanılması sonucu belirlemiyordu. Kumaşın kıvrılma, pile yapma ya da genişleme eğilimi, evrensel geometrik kurallara göre şekilleniyordu. .
Örgü Örmek İle Origami Neden İlişkilidir?
Araştırmacılar, bu çalışmanın daha geniş bir araştırma hattının parçası olduğunu vurguluyor. Bu hattın içinde kirigami de yer alıyor—kağıt ya da ince malzemelerin kesilip katlanarak üç boyutlu, hareketli yapılar haline getirildiği bir teknik. Origamiden farklı olarak kirigami sadece katlamaya değil, aynı zamanda stratejik kesilere de dayanır. Bu kesikler sayesinde yüzey, çekildiğinde ya da büküldüğünde belli şekillere dönüşür.

Kirigami, son yıllarda mühendislik, mimarlık, biyomedikal cihazlar ve yumuşak robotik gibi alanlarda büyük ilgi görüyor. Çünkü bu yöntemle, ince ve hafif malzemelere karmaşık hareketler kazandırmak mümkün oluyor. Yapıya menteşe, yay veya motor eklemeye gerek kalmadan, sadece kesiklerin konumunu ve şeklini değiştirerek malzemenin davranışı kontrol edilebiliyor.
Örgü örmek de benzer bir mantıkla çalışıyor. Kirigami’de yapıya kesikler eklenirken, örmede ilmekler ekleniyor. Her iki durumda da, malzemenin nasıl şekil alacağı geometri yoluyla programlanıyor. Üstelik bu programlama, dışarıdan ısı, menteşe ya da yapısal destek gerektirmeden gerçekleşiyor.
Bu yaklaşımı tanımlamak için araştırmacılar yeni bir kavram önerdi: knitogami™. Origaminin ilkelerini kumaş temelli, yumuşak bir ortama taşıyan bu terim, kendiliğinden şekil alan tekstil malzemelerini tanımlıyor. Kağıttaki kıvrım ve kat izleri yerine, örme ilmeklerinin doğal esnekliği ve yapısı kullanılarak dinamik, form değiştirebilen yüzeyler elde ediliyor.

Araştırma ekibi, bu ilkeleri haritalayarak programlanabilir tekstiller tasarlamaya yönelik bir çerçeve geliştirdi. Bu tür kumaşlar, dış kuvvetlere gerek kalmadan—sadece ilmek deseninin değiştirilmesiyle—belirli şekillere bürünebiliyor. Böylece kumaşın nasıl davranacağı önceden kestirilebiliyor. Bu yaklaşım sayesinde, hareketle uyum sağlayan giysiler, vücuda şekil veren medikal tekstiller tasarlamak olasıdır.
Sonuç Olarak
Araştırma ekibi bir sonraki adımda, geliştirdikleri modeli daha karmaşık ilmek desenlerini ve kumaş davranışlarını kapsayacak şekilde genişletmeyi planlıyor.
Şimdilik odak noktaları temel ilmek türleri—düz ve ters ilmekler. Ancak örme dünyası, burgu ve ajur gibi çok daha çeşitli ve karmaşık tekniklerle dolu. Hedef, bu matematiksel yaklaşımı ileri düzey örme yöntemlerini de içerecek biçimde geliştirmektir.
Kaynaklar ve ileri okumalar
- What can theoretical physics teach us about knitting? Yayınlanma tarihi: 20 Şubat 2025. Kaynak site: Penn Today. Bağlantı: What can theoretical physics teach us about knitting?
- Niu, Lauren & Dion, Genevieve & Kamien, Randall. (2025). Geometric modeling of knitted fabrics. Proceedings of the National Academy of Sciences of the United States of America. 122. e2416536122. 10.1073/pnas.2416536122.
- Zheng M, Chen Y, Liu Z, Liu Y, Wang Y, Liu P, Liu Q, Bi K, Shu Z, Zhang Y, Duan H. Kirigami-inspired multiscale patterning of metallic structures via predefined nanotrench templates. Microsyst Nanoeng. 2019 Dec 2;5:54. doi: 10.1038/s41378-019-0100-3. PMID: 31814993; PMCID: PMC6885514.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel