En sevdiğiniz fonksiyon hangisidir? Eğer cevabınız gamma fonksiyonu değilse, bu yazıyı okuduktan sonra cevabınız değişebilir.

Gamma fonksiyonu 1729 yılında, St. Petersburg’da yaşayan genç bir İsviçreli matematikçi olan Leonhard Euler ile Moskova’daki Alman matematikçi Christian Goldbach arasındaki mektuplaşmalar sırasında doğdu.
Euler henüz 22 yaşındaydı ama kısa sürede 18. yüzyılın en büyük matematikçilerinden biri olacaktı. Goldbach ise çok yönlü bir düşünürdü. Matematikte amatör sayılabilirdi ama geleceğe zor ve önemli problemler bırakan bir zihindi.
Gamma fonksiyonunun ortaya çıkışı birkaç matematik alanının birleşmesiyle mümkün oldu. Bunlardan ilki, 17. yüzyıl İngiliz matematikçilerinin geliştirdiği interpolasyon kuramıydı (interpolasyon: bilinen noktalar arasındaki ara değerleri tahmin etmeye yarayan yöntem).
Bu alan pratiktir ve dönem dönem tüm matematikçilerin ilgisini çekmiştir. İkinci alan ise integral hesabının gelişmesiydi; belirsiz integraller için genel formüller üretme çabası yıllardır sürüyordu.
Goldbach ve Daniel Bernoulli’nin çözemediği bir interpolasyon problemi vardı. Daha önce James Stirling de benzer bir soruyla uğraşmıştı. Sonunda problem Euler’e ulaştı. Euler çözümünü Goldbach’a iki mektupta anlattı; bu mektuplar ömür boyu sürecek bir yazışmanın başlangıcı oldu.
Euler mektuplarda sadece genel fikri vermişti; ancak bir yıl geçmeden tüm ayrıntıları makalesinde yayımladı. Bu çalışma bugün Opera Omnia’da yer alıyor ve Gamma fonksiyonunun doğuşunun temel metinlerinden biri kabul ediliyor.
Gama Fonksiyonu Nedir?
İlginç bir sayı dizisi olarak 1, 1+2, 1+2+3, 1+2+3+4, … dizisine bakalım. Bunlara üçgensel sayılar denir, çünkü farklı boyutlarda üçgen düzenlerine yerleştirilebilecek nesne sayılarını gösterirler. Bu dizinin n’inci terimi Tₙ = ½ n(n+1) formülüyle hesaplanır.
Bu formül, uzun toplama işlemlerini basit bir çarpma ve bölmeye dönüştürür. Örneğin ilk 100 sayıyı tek tek toplamak yerine T₁₀₀ = 5050 sonucuna hemen ulaşırız. Daha ilginci, formül doğal sayıların dışına da taşar.
Örneğin “ilk 5 buçuk tam sayının toplamı nedir?” diye bir soru tam olarak anlamlı değildir. Ama formülü kullanırsak T₅.₅ = ½·(5.5)·(6.5) = 17⅞ sonucunu verir. Yani formül, tanımlandığı doğal sayılar kümesinin ötesine geçer ve ara değerler için de bir karşılık üretir.
Bu da interpolasyonun özüdür: bilinen noktalardan yola çıkarak aradaki değerleri tanımlamak. Bu fikir, gamma fonksiyonunun doğuşunda da temel rol oynamıştır.
Toplamlar yerine çarpmaları düşünmeye başladığımız anda karşımıza başka bir dizi çıkar: faktöriyel dizisi. 1, 1·2, 1·2·3… yani 1!, 2!, 3!… şeklinde ilerleyen bu dizi çok hızlı büyür.
Faktöriyeller matematiğin her alanında karşımıza çıkar. Bu kadar önemli bir dizi için de doğal bir soru doğar. Faktöriyelleri hesaplamak için üçgensel sayılardaki gibi basit bir formül bulabilir miyiz? Ve daha zor bir soru: Faktöriyellerin arasını doldurabilir miyiz? Örneğin 5 buçuğun faktöriyeli ne demektir?
Bu, faktöriyel dizisini ara değerlere genişletme problemidir ve Goldbach, Bernoulli, Stirling gibi matematikçileri uzun süre meşgul etmiştir. Sonunda Euler’e kadar uzanan bu araştırma, gamma fonksiyonunun doğmasına yol açtı. Çünkü anlaşıldı ki, üçgensel sayılar için bulduğumuz kadar basit bir formül faktöriyellerde mümkün değildir.
Faktöriyelin ara değerlere genişletilmesi, “saf cebir”in ötesinde analizin derinliklerine uzanan bir süreç gerektirir. Gamma fonksiyonu tam da bu ihtiyaca verilen cevaptır.
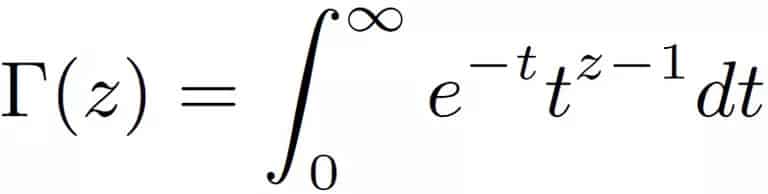
Gama Fonksiyonu Ne İşe Yarar?
Gamma fonksiyonunun en temel özelliği Γ(z + 1) = z Γ(z) bağıntısıdır. z yerine n − 1 yazdığımızda Γ(n) = (n − 1) Γ(n − 1) elde ederiz. Aynı kuralı Γ(n − 1), Γ(n − 2), Γ(n − 3) için tekrar tekrar uygularsak, ifade sonunda şu hale gelir.
Γ(n) = (n − 1)(n − 2)… 2 · 1 · Γ(1).
Tanımdan Γ(1) = 1 olduğu için, bu çarpım tam olarak (n − 1)! değerine eşittir. Böylece Γ(n) = (n − 1)! bağıntısı ortaya çıkar ve gamma fonksiyonunun doğal sayılarda faktöriyelle çakıştığı netleşir. Bu bağlantı, 0! = 1 tanımının neden mantıklı olduğunu da açıklığa kavuşturur.
Gamma fonksiyonunun en etkileyici yanı, yalnızca tam sayılar için tanımlı olmamasıdır. Negatif tam sayılar dışında kalan tüm karmaşık sayılar gamma fonksiyonunun tanım kümesine girer. Bu da faktöriyeli tam sayıların dışına taşıyabileceğimiz anlamına gelir.
Bu genişlemenin en ünlü ve şaşırtıcı sonuçlarından biri şudur: Γ(1/2) = √π.
Benzer biçimde, argüman olarak 1/2’nin tek katlarını verdiğinizde gamma fonksiyonu her zaman π’nin karekökü ile bağlantılı bir değer üretir. Bu da gamma fonksiyonunun gizli bir şekilde geometriyle bağ kurduğunu gösterir.
Sonuç Olarak
Gamma fonksiyonu matematiğin birbirinden çok farklı görünen alanlarında karşımıza çıkar. Bunun en önemli nedeni, faktöriyeli genelleştirmesi sayesinde kombinatorik ve olasılık problemlerinde güçlü bir araç hâline gelmesidir.
Bazı olasılık dağılımları doğrudan gamma fonksiyonu kullanılarak tanımlanır. Örneğin, gamma dağılımı tamamen Γ(z) üzerinden ifade edilir ve deprem gibi olaylar arasındaki zaman aralıklarını modellemede kullanılır.
Aynı şekilde, popülasyonun standart sapmasının bilinmediği durumlarda kullanılan Student’ın t dağılımı ile istatistikte sık geçen ki-kare dağılımı da tanımları gereği gamma fonksiyonuna dayanır. Bu yüzden gamma fonksiyonu, sadece soyut analizde değil, gerçek verileri anlamada da merkezi bir rol oynar.
Kaynaklar ve ileri okumalar:
- What Is the Gamma Function?; Yayınlanma tarihi: 4 Şubat 2018; Bağlantı: https://www.thoughtco.com
- Britannica, The Editors of Encyclopaedia. “gamma function”. Encyclopedia Britannica, 13 Oct. 2023, https://www.britannica.com/science/gamma-function. Accessed 14 January 2024.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi artırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel