Günlük hayatta düğümlerle karşılaşmadığımız bir gün bile yoktur. Ancak insanlar düğüm atmayı öğrenmeden çok önce, doğa bunu zaten yapıyor ve bozuyordu. Bazı DNA türleri, proteinler, manyetik alanlar ve akışkan girdapları zaman zaman halka biçimleri oluşturur ve bu halkalar birbirine dolanabilir. Tüm bunlar, düğüm teorisi kapsamında incelenir.

Düğüm teorisi, evrenin temel yapısını anlamak için ortaya çıktı. 1867’de bilim insanları maddenin çeşitliliğini açıklayacak bir model ararken, İskoç matematikçi ve fizikçi Peter Guthrie Tait, arkadaşı Sir William Thomson’a duman halkaları üreten aygıtını gösterdi.
İleriki yıllarda Kelvin ölçeğine adını verecek olan Thomson, bu halkaların biçimlerine, dayanıklılıklarına ve birbirleriyle etkileşimlerine hayran kaldı. Bu ilgi onu beklenmedik bir düşünceye götürdü. Thomson, farklı atomların aslında, tüm uzayı doldurduğuna inanılan eter içinde düğümlenmiş yapılar olduğunu öne sürdü.
Bugün bu Viktorya dönemi fikri tuhaf görünse de araştırmacılar onu ciddiye aldı. Girdap kuramının güçlü yönleri vardı. Her biri az farklı binbir çeşit düğüm, kimyasal elementlerin çeşitliliğini andırıyordu. Girdap halkalarının kararlı yapısı, atomların neden kalıcı olduğunu da açıklayabilirdi.

Düğüm kuramı bilim dünyasında ilgi gördükçe Tait tüm düğümleri kaydetmeye başladı. 1880’lerin sonuna gelindiğinde Thomson kuramından uzaklaşmıştı. Buna rağmen Tait, çalışmasını sürdürdü. Böylece düğüm teorisi adıyla bilinen matematiksel alanı kurdu.
Düğüm Teorisi Nedir?
Hepimiz düğümlere aşinayız. Ancak bu bildiklerimiz, Tait’in ve diğer matematikçilerin düğüm olarak tanımladığı yapılar değildir. Matematiksel bir düğüm elde etmek için ipin iki ucunu birleştirip kapalı bir halka oluşturmak gerekir.
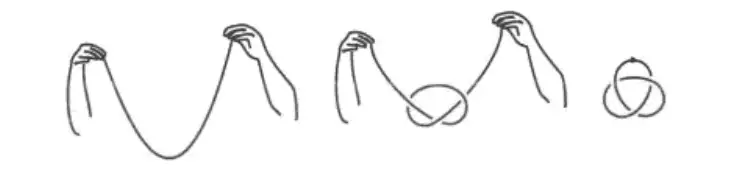
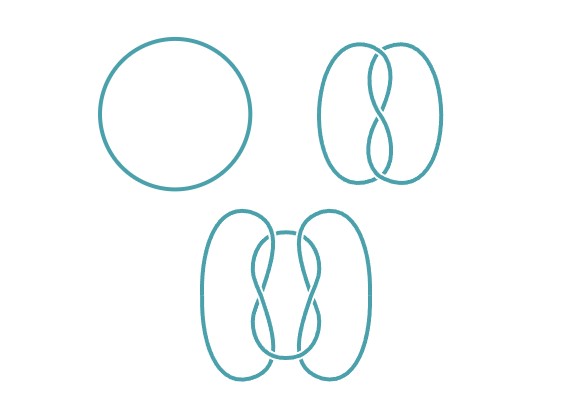
Bir düğümün yapısı ip gibi esnek olduğu için matematikçiler bu alanı, biçimlerin eğilip bükülebilirliğini inceleyen topolojinin bir alt dalı olarak görür. Bazen bir düğümü açıp onu basit bir çembere dönüştürmek mümkündür; buna çözülmüş düğüm deriz. Ama çoğu zaman bir düğümü açmak imkânsızdır.
Thomson ve Tait düğümlerle ilgili çalışmalar yapan ilk kişiler değildi. 1794’te Gauss, defterinde düğümler üzerine notlar almış ve örnekler çizmişti. Gauss’un öğrencisi Johann Listing ise 1847’de yayımladığı Vorstudien zur Topologie adlı çalışmasında düğümlerden söz etmişti. Aslında topoloji teriminin kökeni de buraya dayanır.
Yine de düğüm kuramının temel sorununu ele alan ilk kişi Tait oldu. Bu temel sorun tüm olası düğümlerin sınıflandırılması ve kaydedilmesiydi. Yıllar boyunca yalnızca kendi geometrik sezgisine güvenerek çalıştı ve düzleme yansıtıldığında en fazla yedi kesişme noktası bulunan tüm asal düğümleri bulup sınıflandırdı.
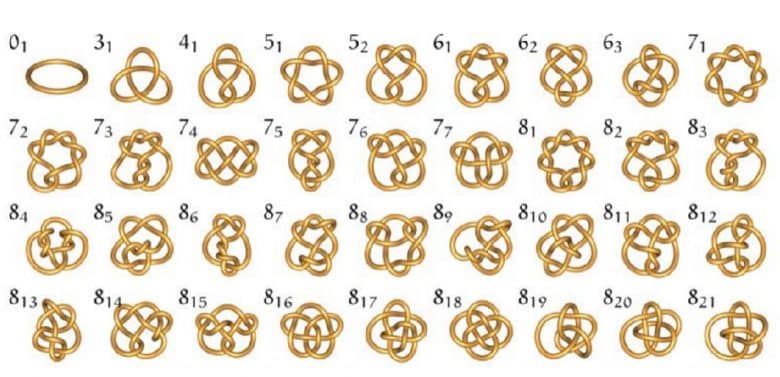
19. yüzyılın sonunda Tait, Kirkman ve Little’ın da düğümlerin sınıflandırılması üzerine çalıştığını öğrendi. Üçü birlikte en fazla on kesişmesi olan tüm asal düğümleri ve on bir kesişmesi olanların çoğunu eksiksiz biçimde kaydetti.
Son yüzyılda matematikçiler, iki düğümün gerçekten aynı mı yoksa farklı mı olduğunu anlamak için birçok akıllı yöntem geliştirdi. Bunun yolu, düğüme özgü bir özellik bulmaktan geçer. Bu özelliğe değişmez denir; çünkü düğümü nasıl çekip çevirirseniz çevirin değişmez.
Ama bu özellikler her zaman kesin ayrım yapmaz; bazen iki farklı düğüm aynı değere sahip olur. . Bu yüzden düğümlerin tam listesi hâlâ tamamlanmamıştır.
Düğüm Teorisi Nerelerde Karşımıza Çıkar?
Düğüm kuramı yüzyıllar içinde matematiğin farklı alanları arasında dolaştı. Başlangıçta uygulamalı bir alan olarak ortaya çıktı; Thomson maddeyi anlamak için düğümleri kullanmaya çalışıyordu. Bu fikir zamanla terk edilince düğüm kuramı saf matematiğin bir parçasına, topolojinin ilgi çekici ama uzun süre uygulama alanı bulunmayan bir dalına dönüştü. Son yıllarda ise yeniden uygulamalı bir alan hâline geldi.
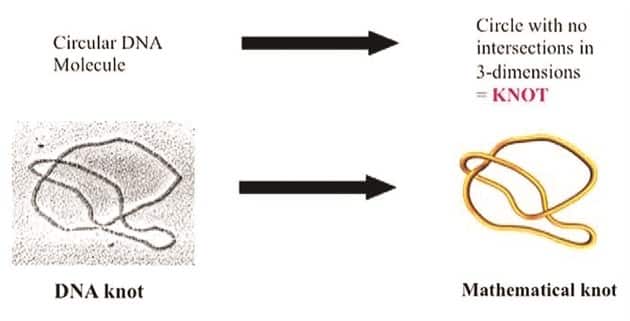
Araştırmacılar akışkanların davranışından elektrodinamiğe, DNA gibi düğümlenen moleküllerden başka birçok yapıya kadar pek çok konuyu incelerken düğüm kuramından yararlanıyor. Neyse ki bilim insanları farklı şeylerle uğraşırken matematikçiler düğümlerin kataloglarını hazırladı ve onların sırlarını çözmek için gerekli araçları geliştirdi.
Kaynaklar ve ileri okumalar:
- Stolz, R., Yoshida, M., Brasher, R. et al. Pathways of DNA unlinking: A story of stepwise simplification. Sci Rep 7, 12420 (2017). https://doi.org/10.1038/s41598-017-12172-2
- Untangling Why Knots Are Important. Kaynak site: Quanta Magazine. Yayınlanma tarihi: 11 Ekim 2022. Bağlantı: Bağlantı: Untangling Why Knots Are Important./
- Alekseev, Ilya & Malyutin, Andrey & Vershik, Anatoly. (2025). On the growth of the number of prime knots. St Petersburg Mathematical Journal. 36. 9-24. 10.1090/spmj/1844.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






Nesibe Hanım
Çok güzel bir derleme , tebrik ederim .
Teşekkürler.