Büyük sayılar yasası, olasılık teorisinin en temel teoremlerinden biridir. Bu yasa, bir olasılık süreci çok sayıda tekrarlandığında, olası sonuçların göreli sıklıklarının kendi gerçek olasılıklarına giderek daha fazla yaklaşacağını söyler.
Adil bir madeni parayı havaya attığımı zaman yazı ve tura gelme olasılığının yarı yarıya olduğunu biliriz. Ancak bir çok kişi “Neden yarı yarıya?” sorusunun cevabını vermekte zorlanacaktır. Gerçekte, yazı tura atarken yazı gelme olasılığının tam olarak yarı yarıya olduğunu kesin biçimde bilemeyiz.
Bunu anlamak için küçük bir deney yapalım. Boş zamanı bol birinden rica edip uzun süre boyunca para atmasını isteyelim. Bu işi birçok kez tekrarlamak gerekir. Çünkü deneme sayısı az olursa tesadüfler sonucu büyük ölçüde etkileyecektir.
Örneğin bir parayı yalnızca altı kez attığımızda, para tamamen dengeli olsa bile sonuçlar çok değişken olur. İki kez yazı, dört kez tura gelebilir ya da üçe üç eşit dağılabilir. Ancak paranın gerçekten adil olduğunu varsayarsak ve bin kez atarsak, yazı ile tura sayıları yaklaşık olarak beş yüzer civarında olur.
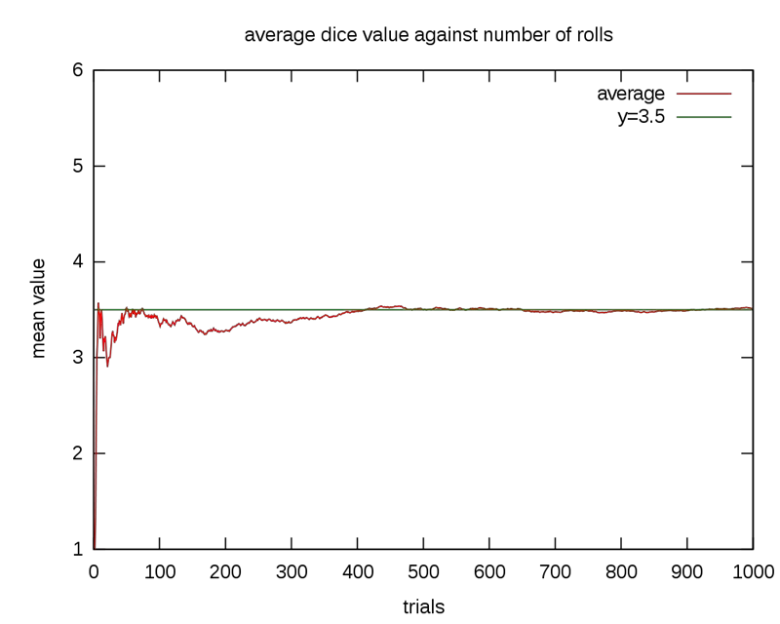
Uzun vadede, beklenen sonuç gerçeğe giderek yaklaşır. Bu da büyük sayılar yasasının tam olarak söylediğidir: Denemeler çoğaldıkça, olasılıklar kendilerini istatistiksel olarak doğrular. Bu yasa, bugün kumarhanelerin servet kazanmasını sağlayan matematiksel temellerden biridir.
Büyük Sayılar Yasası Nedir?
Jacob Bernoulli, matematik dünyasında gerçek bir yıldızdı. Kendisi ayrıca, istatistik ve olasılık teorisinin en temel kurallarından biri olan büyük sayılar yasasının kanıtını bulan ilk kişiydi. Bernoulli bu kanıtı Ars Conjectandi adlı kitabında yayımladı. Ancak kitap 1713 yılında, onun ölümünden sekiz yıl sonra basıldı. Eseri, kendisi gibi önemli bir matematikçi olan yeğeni Nicolaus Bernoulli yayımladı.
“Büyük sayılar yasası” terimini ortaya atan kişi ise Jacob Bernoulli değildi. Bu adlandırma, Fransız soylusu ve matematikçi Siméon Denis Poisson’a aittir.

Bu yasa der ki, eğer adil bir parayı N kez atar ve bu atışlarda yazı K kez gelirse, N büyüdükçe K/N oranı ½ değerine giderek daha fazla yaklaşır.
Büyük sayılar yasası, bir parayı birçok kez attığımızda yazı ve tura sayıları arasındaki farkın sıfıra yakın olacağını söylemez. Yasanın söylediği şey, yazıların ve turaların oranının ½’ye yaklaşacağıdır.
Diyelim ki adil bir parayı bir milyon kez attık ve sonuç şöyle oldu: 500.800 kez yazı, 499.200 kez tura geldi. Aradaki fark 1.600’dür, yani yazı 1.600 kez daha fazla gelmiştir. Büyük sayılar yasası için bu fark önemli değildir. Yasa yalnızca, yazı sayısının toplam atış sayısına oranının ½’ye çok yakın olacağını garanti eder. Gerçekten de 500.800 / 1.000.000 = 0,5008 yapar. Bu değer 0,5 yani ½’ye oldukça yakındır.
Bir zar attığımızda 4 gelme olasılığı 1/6’dır, çünkü zarın altı yüzünün her biri eşit şansa sahiptir. Büyük sayılar yasası, zarı çok sayıda attığımızda (örneğin 600 kez) 4’ün yaklaşık 100 kez gelmesini beklememiz gerektiğini söyler. Buradaki “yaklaşık” ifadesi önemlidir, çünkü 1’den 6’ya kadar her sonucun tam olarak 100’er kez gelmesi son derece düşük bir olasılıktır.
Büyük Sayılar Yasasının Algılarımız Üzerine Etkileri
Büyük sayılar yasası, kendi içinde bir tür paradoks taşır. Hiç kimse tek bir yazı tura atışının sonucunu bilemez. Ancak istatistikçiler, tek tek atışlar hakkında hiçbir bilgiye sahip olmadan, 10.000 atışın genel sonucunu şaşırtıcı bir doğrulukla tahmin eder. Oldukça basit görünen bu yasa, tarih boyunca birçok yanlış anlamanın kaynağı olmuştur.
Avrupa ruletinde 18 kırmızı, 18 siyah ve 0 numaralı yeşil bir kutu vardır. Bir renge bahis yapmak yazı tura oynamaya benzer, ancak kumarhaneler küçük bir fark sayesinde kazanır: Bir rengi doğru tahmin etme olasılığı 18/37’dir, yani yarıdan biraz daha azdır.
İşte bu “biraz az” fark, büyük sayılar yasasıyla birleştiğinde kumarhaneler için sürekli gelir kaynağı, kumar bağımlıları içinse bitmek bilmeyen bir hayal kırıklığı haline gelir.
Kısacası, kumarhanede para kazanabilirsiniz. Ta ki bağımlı oluncaya kadar. Çünkü çok oynamaya başladığınız anda, büyük sayılar devreye girer. Sizden yana olmayan olasılıkların sonucu kaçınılmaz hale gelir. Uzun vadede her zaman kaybedersiniz.
Sonuç Olarak
Diyelim ki Monte Carlo’daki bir kumarhaneye 5 dolar ile gittiniz ve bunu 10 dolara çıkarmak istiyorsunuz. Size önerim, tüm paranızı kırmızıya (ya da isterseniz siyaha) yatırmanız olur. Tüm parayı tek elde oynamak, yani 5 doları bir kerede riske atmak aslında yapabileceğiniz en akıllıca hamledir. Çünkü, ne kadar az oyun oynarsanız o kadar iyidir.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Expectation; yayınlanma tarihi: 20 Mayıs 2016; Bağlantı: https://plus.maths.org/
- What is financial mathematics?; yayınlanma tarihi: 1eylül 2009; Bağlantı: https://plus.maths.org/
- Falk, Ruma & Lann, Avital. (2013). Numbers defy the law of large numbers. Teaching Statistics. 37. 10.1111/test.12031.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel