Kepler denildiğinde genellikle akla ünlü Kepler yasaları veya Kepler varsayımı gibi kavramlar gelir. Gerçekten de Kepler, kendine özgü bilimsel tutkusu ve dehasıyla astronomiye modern niteliğini kazandıran kişidir.

Daha az bilinen ise Kepler’in matematiğe yaptığı katkılardır. Aslında, Gottfried Leibniz ve Isaac Newton tarafından geliştirilen integralin temellerini atan kişi Kepler’dir. Ancak bu çalışmasını bilimsel bir atılımdan çok, şaraba duyduğu ilgi sayesinde gerçekleştirmiştir.
İlham anı ise 1600’lerin başında, Avusturya’da Kepler’in ikinci eşi Susanna Reuttinger ile evleneceği sıralarda gelmiştir.
Newton ve Leibniz’den önceki yüzyılda, Yunan matematikçilerin, özellikle de Arşimet’in, çalışmaları oldukça popülerdi. Bu dönemde alan ve hacim hesaplamaları genellikle sonsuz küçükler hesabı adı verilen yöntemle yapılırdı.
Kepler’in alan ve hacim hesaplamalarına olan ilgisi ise, düğün hazırlıkları sırasında yaşanan bir olayın sonucunda şekillendi. Hikâyenin detayları aşağıdaki şekilde rivayet edilmektedir:
Kepler Neden Bir Şarap Fıçısının Hacmini Hesaplamak İstemişti?

Johannes Kepler’in ilk eşi Barbara Müller, 1611 yılında vefat etti. Daha sonra, 1613 yılında Kepler, Susanna Reuttinger adında bir kadınla evlendi. Düğün için bir fıçı şarap satın almıştı. Ancak sipariş ettiği şarabı kontrol etmek istediğinde, şarap tüccarının kullandığı hacim ölçüm yöntemi Kepler’e güven vermedi.
Fıçının içindeki şarap miktarını belirlemek için tüccar, işaretli bir çubuğu fıçının yan tarafındaki delikten içeri sokmuş ve çubuğu varilin tabanına ulaşana kadar hareket ettirmişti. Ardından da çubuğun üzerindeki işaretlere bakarak şarabın miktarını ve dolayısıyla fiyatını belirlemişti.
Bir matematikçi, bilim insanı ve dikkatli bir gözlemci olarak bu durum Kepler’i şaşırttı. Sonuçta, tüm şarap fıçıları aynı şekil veya boyutta olamazdı. Bu nedenle, kullanılan yöntemin son derece hatalı bir ölçüm biçimi olduğunu düşünerek, bir fıçının içindeki şarabın hacmini belirlemenin daha doğru yollarını araştırmaya başladı.

Nihayetinde, bulgularını 1615 yılında Nova Stereometria Doliorum Vinariorum (Şarap Fıçılarının Yeni Katı Geometrisi) adlı eserinde yayımladı. Kepler’in sorduğu “Bir fıçının hacmini maksimuma çıkarmak için en iyi tasarım nedir?” sorusunun cevabını bugün, türev kavramı yardımıyla verebiliyoruz.
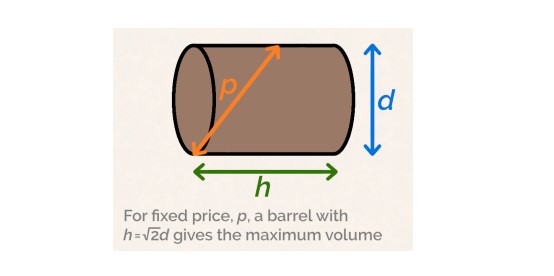
Kepler Şarap Fıçısının Hacmini Nasıl Hesapladı?
Bir şarap fıçısının hacmini doğru şekilde belirlemek için Kepler, dolu bir fıçıdaki şarabın, katmanlar hâlinde düzenlenmiş çok sayıda ince tabakadan oluştuğunu varsaydı. Bu tabakaların her biri, birer silindir gibi düşünülmeliydi.
Toplam hacmi bulmak için yapması gereken şey, bu dilimlerin hacimlerini tek tek hesaplayıp toplamaktı. Dilimler ne kadar ince olursa, elde edilen sonuç da o kadar doğru olacaktı.
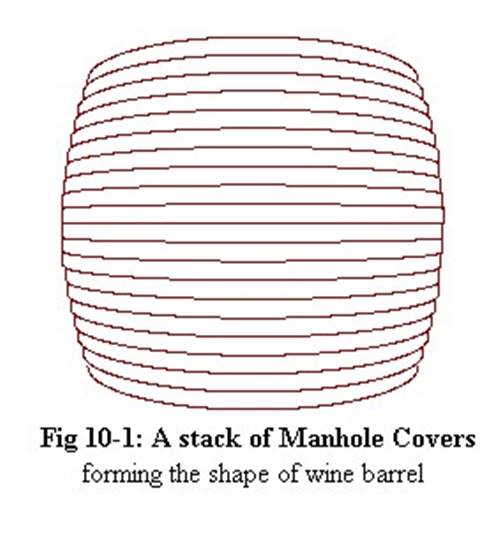
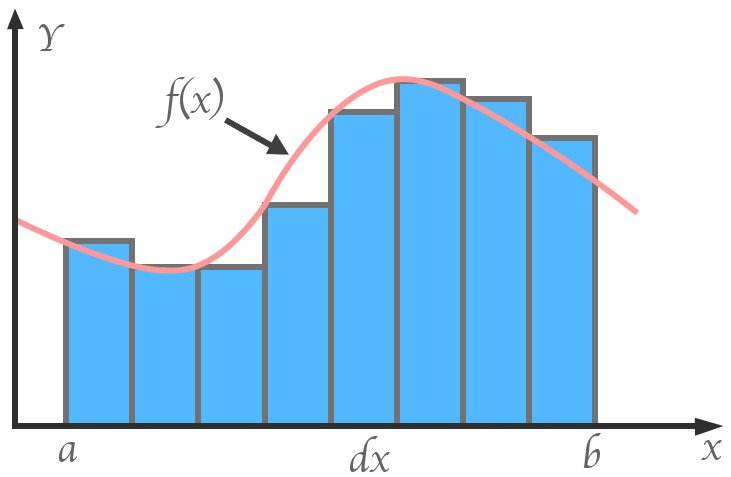
İntegral hesabına aşina olanlar, Kepler’in yaklaşımının günümüzde kullandığımız tanımla büyük benzerlik taşıdığını fark edecektir. Bir fonksiyonun integralini hesapladığımızda, aslında fonksiyona karşılık gelen eğrinin altındaki alanı bulmuş oluruz.
Bunu da, tıpkı Kepler’in yaptığı gibi, eğriyi sonsuz derecede küçük tabanlara sahip dikdörtgenlere bölerek yaparız. Dikdörtgenler ne kadar ince olursa, elde edilen sonucun doğruluğu da o kadar artar. Bir dikdörtgenin alanı, iki dik kenarının çarpımıyla bulunur. Bu mantıkla yapılması gereken şey, her dikdörtgenin alanını tek tek hesaplamak ve ardından bu alanları toplamaktır.
Sonuç olarak
Matematik tarihçileri Nova Stereometria Doliorum Vinariorum’u kalkülüsün gelişimine önemli bir katkı olarak kabul etmektedir. Ancak bu değeri takdir edenler yalnızca tarihçiler değildir.

Kitabın, 17. yüzyılın başlarında Avusturya’nın Linz kentinde basılan ilk baskısı, koleksiyonerler için de oldukça değerliydi. Nitekim bir kopyası, 2019 yılında 32.500 dolara alıcı bularak bu ilginin somut bir göstergesi olmuştur.
Kaynaklar ve ileri okumalar
Roberto Cardil (MatematicasVisuales). “Kepler: The Volume of a Wine Barrel.Solving the Problem of Maxima: Wine Barrel Design.” Convergence (January 2012), DOI:10.4169/loci003499
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel