1990’larda çocuk olan biri için Tetris’ten kaçmak mümkün değildi. Rus programcı Alexey Pajitnov’un 1984’te geliştirdiği bu oyun, kısa sürede bir fenomene dönüştü ve yıllar içinde yüz milyonlarca kişi tarafından oynandı.

Ocak 2024’e kadar kimse Tetris oyununu bitirememişti. Oklahoma’lı bir genç, 157. seviyede oyunu çökertmeyi başararak bunu ilk yapan kişi oldu. Oyunculara taşları daha hızlı ve verimli yerleştirme konusunda taktikler sunan yapay zekâ algoritmaları, bu başarıda önemli bir rol oynadı. Bu stratejiler sayesinde, Tetris sonunda ilk kez bir oyuncuya “yenik düştü.”
Ancak Tetris’in amacı sadece “kazanmak” değildir. Tetris yalnızca bir refleks oyunu değildir; aynı zamanda zihinsel bir egzersizdir. Her hamlede, beynin şekilleri döndürme, hizalama ve önceden planlama yeteneği devreye girer. Bu nedenle Tetris, eğlencenin ötesinde, geometriyle düşünmenin canlı bir örneğidir.

Tetris Oyunu Matematikçiler İçin Neden Önemlidir?
Aslında tüm oyunları matematiksel açıdan incelemek mümkündür.. Ancak Tetris’in matematikle çok özel bağları vardır. Oyunun temel amacı, geometrideki “paketleme” (ya da döşeme) problemlerini andırır. Bu problemler, bir alanın boşluk bırakmadan, sonsuz sayıda karo ile kaplanıp kaplanamayacağını araştırır.
Tetris’i matematikçiler için asıl ilginç kılan şey ise karmaşıklığıdır. Araştırmacılar uzun süredir, Tetris’in gerçekten “çözülüp çözülemeyeceğini” anlamak için gereken hesaplama gücünü sorguluyor. Belirli koşullar altında—örneğin sınırlı sayıda blok ve blokların hangi sırayla düşeceğini bilme olasılığı gibi—bu sorunun cevabını bulmak, Tetris’i matematiksel olarak en karmaşık oyunlardan biri haline getiriyor.
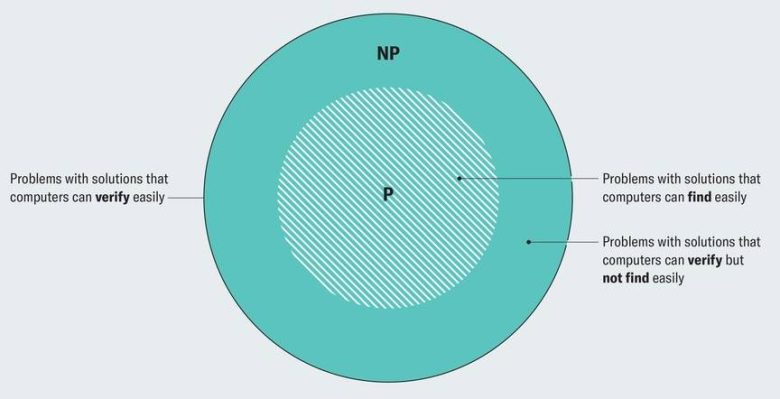
Karmaşıklık kuramı alanında matematikçiler ve bilgisayar bilimciler, bir problemi çözmenin ne kadar zor olduğunu anlamaya çalışır. Bunun için “karmaşıklık sınıfları” denen kategoriler tanımlanmıştır. Bunların en bilinenleri P ve NP sınıflarıdır.
Basitçe anlatmak gerekirse, P sınıfındaki problemler klasik bilgisayarlar tarafından kolayca çözülür. NP sınıfındaki problemler ise çözmesi zor ama çözüm bulunduğunda kontrol etmesi kolay problemlerdir.
Bir görevin ne kadar karmaşık olduğunu belirlemek için, farklı problemleri birbirleriyle karşılaştırmak gerekir. Örneğin, eğer A görevini çözen her algoritma B görevini de çözebiliyorsa, o zaman A, B’den daha karmaşıktır. Bu yöntemle, Tetris’i bir P ya da NP problemiyle karşılaştırarak oyunun karmaşıklığını anlamak olasıdır.
Peki bir karşılaştırma noktası nasıl seçmeliyiz? Bilgisayar bilimciler, bunun için “NP-tam” adı verilen özel problemlere bakar. Bu problemler, tüm NP problemlerine indirgenebildiği için karmaşıklığın ölçülmesinde temel bir referans oluşturur. En bilinen örneklerinden biri “üçlü bölme problemidir.”
Üçlü Bölme Problemi Nedir?
Üçlü bölme problemi, verilen bir sayı kümesinin üçer elemanlı alt kümelere eşit toplamlarla ayrılıp ayrılamayacağını sorgular. Örneğin {1, 2, 5, 6, 7, 9} kümesi, {1, 5, 9} ve {2, 6, 7} biçiminde iki alt kümeye ayrılır. Çünkü her biri toplam15 eder. Ancak her sayı kümesi için böyle bir bölme mümkün değildir. Bu tür bir ayrımın mümkün olup olmadığını bulmak son derece zordur. İşte bu nedenle, üçlü bölme problemi NP-tam sınıfına girer.
2003 yılında Massachusetts Teknoloji Enstitüsü’nden bir grup bilgisayar bilimci, Tetris tahtasının tamamen temizlenip temizlenemeyeceği sorusunun aslında üçlü bölme problemiyle aynı türden bir matematiksel soru olduğunu gösterdi. Bunu yapmak için, Tetris oyunundaki boşlukları üçlü bölme problemindeki alt kümelere, düşen blokları ise bu kümelere dağıtılması gereken sayılara benzettiler.
Sonuçta şu sonuca vardılar. Eğer sayı kümesi üçer elemanlı alt kümelere eşit toplamlarla bölünebiliyorsa, Tetris tahtası da tamamen temizlenebilir. Yani “Bir küme eşit toplamlı üçlü gruplara ayrılır mı?” sorusu ile “Tetris tahtası tamamen boşaltılır m?” sorusu matematiksel olarak aynı şeydir.
Bu durumda, Tetris oyunu, matematiksel olarak son derece karmaşık bir oyundur. Bu da onun, NP-tam problemler sınıfına girdiğini gösterir.
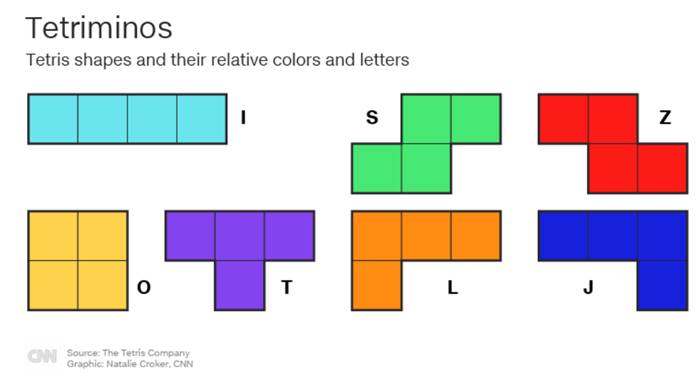
Tetris’in bazı versiyonları öyle karmaşıktır ki, hiçbir bilgisayar bunları tamamen çözemez. Leiden Üniversitesi’nden iki araştırmacı, yalnızca I şeklindeki uzun blokların kullanıldığı bir Tetris oyununu inceledi. Elinizde 40 I şeklindeki bloğun boş bir tahtaya düşebileceği sekiz farklı dizilim olduğunu varsayalım. Bu dizilimlerden birinin tahtayı tamamen boş bırakıp bırakmayacağını belirleyebilir miydiniz?
Bilim insanları bu sorunun karar verilemez olduğunu kanıtladı. Yani, ne kadar güçlü olursa olsun hiçbir bilgisayar bu soruya her durumda yanıt veremez. Elbette bu karmaşık matematiksel sorular, Tetris oynarken başarınızı etkilemez. Çünkü bloklar düşerken düşünmeye zaman kalmaz.
Sonuç Olarak
Yine de Tetris’in 40 yılı aşkın süredir hem popülerliğini hem de hayranlığını koruması dikkat çekici. Oyun özü aynı kalırken, oynanış biçimleri gelişmeye devam ediyor. “Rolling” adı verilen yeni bir teknik, oyuncuların çok daha yüksek seviyelere ulaşmasını sağladı. Sonucunda 29. seviyenin geçilmesinin arka planında da bu teknik vardı.
Kaynaklar ve ileri okumalar
- Anyone can play Tetris. But architects, engineers and animators alike use the math concepts underlying the game. Yayınlanma tarihi: 28 Şubat 2024. Kaynak site: Conversation. Bağlantı: Anyone can play Tetris. But architects, engineers and animators alike use the math concepts underlying the game.
- De Lisi R, Wolford JL. Improving children’s mental rotation accuracy with computer game playing. J Genet Psychol. 2002 Sep;163(3):272-82. doi: 10.1080/00221320209598683. PMID: 12230149.
- Cherney, I.D. Mom, Let Me Play More Computer Games: They Improve My Mental Rotation Skills. Sex Roles 59, 776–786 (2008). https://doi.org/10.1007/s11199-008-9498-z
Matematiksel