Ünlü fizikçi Richard Feynman’ın ortaya koyduğu yol integrali (path integral) fizikçiler için kehanet formülüdür. Çünkü bu integral, gerçekliğimizin tüm olası sonuçların bir toplamı olduğunu söyler.

Fiziğin en güçlü formüllerinden biri ince bir S ile başlar; bu harf integral işaretidir ve bir sistemin bütün olası davranışlarını hesaba katan özel bir toplam türünü gösterir. Ardından gelen ikinci S, fiziğin temel niceliklerinden biri olan eylemi ifade eder. Eylem, bir sistemin zaman içindeki hareketini tek bir büyüklükte özetler.
Bu iki S birleştiğinde, bir parçacığın nasıl davranacağını belirlemek için tüm olası yolları değerlendiren güçlü bir yöntem ortaya çıkar. Bu yöntem Feynman yol integrali olarak bilinir.
Yol integralleri kimi fizikçilere göre hayalci bir yaklaşım gibi görünür ve herkes bu yöntemi benimsemez. Yine de Richard Feynman’ı üne kavuşturan bu fikir, kuramsal fizikçilerin özellikle sevdiği ve sıkça kullandığı bir araçtır.

Feynman Yol İntegrali Nedir?
Kuantum mekaniği 1926’da, Erwin Schrödinger dalga benzeri parçacık durumlarının zaman içinde nasıl değiştiğini tanımlayan denklemi geliştirdiğinde yükselişe geçti. Bir sonraki on yılda Paul Dirac kuantum dünyasına alternatif bir bakış sundu.
Çalışması, A noktasından B noktasına giden şeylerin “en az eylem” yolunu seçtiği fikrine dayanıyordu. Bu kaba bir ifadeyle en az zaman ve enerji gerektiren yol anlamına geliyordu..
Başta yalnızca bir dipnot olarak görünen bu fikir, Richard Feynman tarafından benimsenince büyük bir başarıya dönüştü. Feynman fikri geliştirdi ve 1948’de yol integralini ortaya koydu.
Bu yaklaşımın özü çift yarık deneyinde açıkça ortaya çıkar. Fizikçiler iki yarık bulunan bir perdeye parçacık gönderir ve arkadaki ekranda nereye düştüklerine bakar.
Eğer parçacıklar küçük mermiler gibi davransaydı, ekranda her yarığın arkasında iki yoğun bölge oluşurdu. Oysa ekranda düzenli aralıklarla sıralanan parlak ve karanlık şeritlerden oluşan bir dalga deseni belirir. Bu, yarıklardan geçen şeyin tek bir parçacığın keskin bir izi değil, parçacığın tüm olası konumlarını temsil eden bir dalga olduğunu gösterir.
Yol integrali bu tabloyu genelleştirir. Parçacık A’dan B’ye giderken tek bir yol seçmez; aynı anda tüm olası yolları dener. Feynman’ın yöntemi her yol için bir genlik hesaplar ve bu genlikler toplandığında klasik dünyada gözlediğimiz tek sonuç ortaya çıkar. Engeller olmadığında parçacık ekranda tek bir noktada belirir. Kuantum davranışının bu radikal yorumu, gerçeğin tüm olası yolların toplamıyla belirlendiğini gösterir.
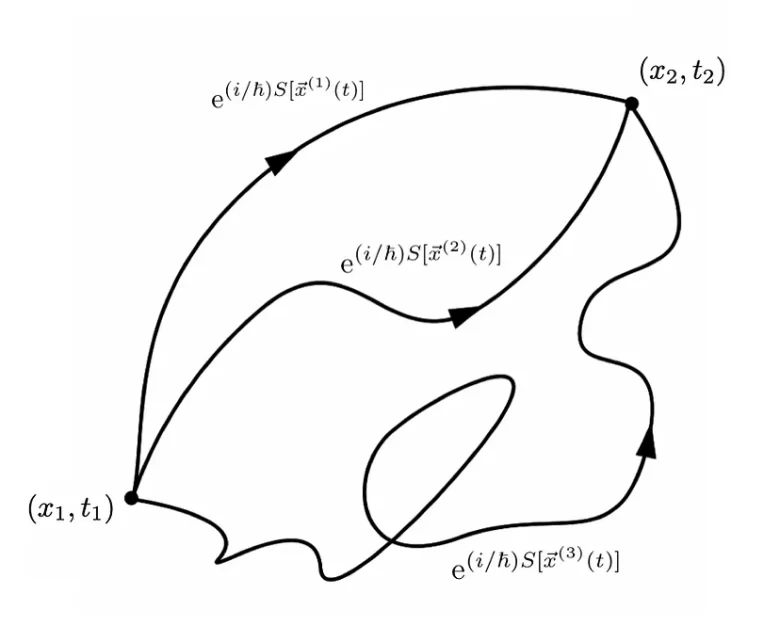
Her yol için bir karmaşık sayı atanır; buna eylem denir. Bir yol ne kadar çok kıvrım ve sapma içerirse, bu sayı o kadar büyür. Klasik fiziğe göre bir parçacık en az eylemli yolu seçer. Kuantum fiziğinde ise parçacık aynı anda tüm yolları izler. Karmaşık sayılar sayesinde de parçacığın belirli bir noktada bulunma olasılığını tam olarak hesaplamak mümkün olur.
Gerçekliğimiz Tüm Olası Gerçekliklerin Toplamı mı?
Fizikçiler parçacıkları zamanla kuantum alanlarındaki uyarımlar olarak görmeye başladı. Bu alanlar, uzayın her noktasında bir değeri olan varlıklardır. Bir parçacık farklı yollar boyunca bir yerden başka bir yere hareket edebilirken, bir alan aynı anda farklı yerlerde dalgalanabilir.
Neyse ki yol integrali kuantum alanları için de çalışır. Connecticut Üniversitesi’nden parçacık fizikçisi Gerald Dunne bunu şöyle özetler: “Ne yapılacağı aslında açıktır. Tüm yolları toplamak yerine, alanın tüm olası düzenlerini toplarsınız.” Önce alanın başlangıç ve bitiş durumlarını belirlersiniz, sonra bu iki durumu birbirine bağlayabilecek her olası gelişimi hesaba katarsınız.
Feynman yol integralini 1949’da elektromanyetik alanın kuantum teorisini geliştirmek için kullanmıştı. Daha sonra başka fizikçiler farklı kuvvetleri ve parçacıkları temsil eden alanlar için eylemleri ve genlikleri nasıl hesaplayacaklarını ortaya koydu.
Sonuç Olarak;
Günümüz fizikçileri, Avrupa’daki Büyük Hadron Çarpıştırıcısı’nda gerçekleşen çarpışmaların sonuçlarını tahmin ederken hesaplamalarını sık sık yol integrali üzerine kurar. Hatta çarpıştırıcının hediyelik eşya dükkânı, bu yöntemin temel bileşeni olan kuantum alanlarının eylem formülünü taşıyan kupalar bile satar.

Yol integrali fizik alanında büyük başarı sağlasa da matematikçileri rahatsız eder. Çünkü uzayda hareket eden tek bir parçacık bile sonsuz sayıda olası yol izler. Kuantum alanları işi daha da karmaşık hale getirir. Alanın her noktası bir değere sahiptir ve bu değer her konumda sonsuz farklı biçimde değişir.
Fizikçiler bu sonsuzluklarla başa çıkmak için çeşitli incelikli yöntemler geliştirmiştir. Fakat matematikçiler bu kadar sınırsız bir ortamda yol integralinin aslında düzgün tanımlanmadığını savunur.
Kaynaklar ve İleri Okumalar
- How Our Reality May Be a Sum of All Possible Realities. Bağlantı: How Our Reality May Be a Sum of All Possible Realities. Quanta Magazine. Yayınlanma tarihi: 6 Şubat 2023
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel