Dünyada mı daha çok kum tanesi var, yoksa evrende mi daha çok yıldız? Berrak bir gecede gözle birkaç bin yıldız görebilirsiniz. Dünya ise çölleri ve sahilleriyle akıl almaz miktarda kum barındırır. Peki sayı yarışını kim kazanır: kumlar mı yoksa yıldızlar mı?

Hawaii Üniversitesi’nde 2003 yılında yapılan bir çalışma, dünyadaki kum tanelerinin sayısını 7.5 milyon trilyon olarak tahmin etti. Bu sayı, 75’in yanına 17 sıfır eklemek demektir. Yıldızlar için yaptıkları tahmin ise gözlemlenebilir evrenin tamamı boyunca 70 bin milyon trilyon oldu. Başka bir ifadeyle, her bir kum tanesi için yaklaşık on bin yıldız vardır.
Yunan matematikçi ve bilim insanı Arşimet de bu tür sorularla ilgilenmişti. MÖ üçüncü yüzyılda Syracuse Kralı Gelon’a hitaben kısa bir risale yazdı. Bugün “Kum Sayacı (The Sand Reckone) ” adıyla bilinen bu metin, hem kesinliği hem de açık dili nedeniyle bazen ilk bilimsel makale olarak anılır. Arşimet bu metinde şu soruyu sorar: Evrene kaç kum tanesi sığar?

Arşimet Kum Tanesi Sayısını Nasıl Hesapladı?
Bir kum tanesinin boyutu ve evrenin büyüklüğü sorunun cevabını belirler. Arşimet, oldukça cömert ve aslında gerçekçi olmayan bir varsayımla, bir haşhaş tohumuna on bin kum tanesinin sığabileceğini düşündü.
Ayrıca kırk haşhaş tohumunun yan yana geldiğinde bir Yunan parmağı genişliğine, yani yaklaşık on dokuz milimetreye ulaştığını hesapladı. Buna göre bir parmak genişliğindeki bir küre yaklaşık altı yüz kırk milyon kum tanesi alabilirdi.
Evrenin büyüklüğüne gelince, Arşimet hesabını Aristarkus’un Güneş merkezli modeline dayandırdı. Bu modele göre Dünya Güneş’in etrafında dönerken yıldızlar çok daha uzakta yer alan büyük bir küreye sabitlenmiştir. Bu bilgi Arşimet’e evrenin bilinen en küçük çapını verdi: modern ölçülerle yaklaşık iki ışık yılı.
Bugün basit bir hesap yaparak Arşimet’in büyüklüğündeki kum tanelerinden iki ışık yılı genişliğindeki bir küreye kaç tane sığacağını bulabiliriz. Sonuç, 1’in yanına 63 sıfır eklenmesiyle elde edilen dev bir sayıdır. Ancak Arşimet’in döneminde bu tür büyük sayıları yazmak için bizim sahip olduğumuz gösterim yöntemleri yoktu. Bugünkü üstel gösterim de o dönemde yoktu.
Arşimet hesaplamalarına başladığında Yunanlar rakamları harflerle gösteriyordu. Alfabenin farklı harfleri 1 ile 9 arasındaki değerleri, onlar basamağındaki ve yüzler basamağındaki karşılıklarını temsil ediyordu. Daha büyük sayılar için harflere ek işaretler konuyordu. En büyük tek birim “murious” yani bizim 10.000 sayımıza karşılık gelen bir değerdi. Romalılar buna “myriad” diyordu.
Arşimet’in Yeni Sayı Sistemi: Canavar Sayılar
Arşimet, kozmik kum hesabını yapabilmek için yeni bir sayı adlandırma sistemi geliştirmesi gerektiğini fark etti. Önce 10.000 × 10.000’e kadar olan tüm sayıları birinci düzen olarak tanımladı. Bugün bunu kolayca 10 üzeri 8 şeklinde yazabiliriz.
Ardından birinci düzenin üstündeki sayıları ikinci düzen olarak belirledi. Her yeni düzen bir öncekinin 10.000 × 10.000 katıydı. Bu şekilde devam ederek birinci dönemi tanımladı. Bu dönemin sonunda ulaştığı en büyük sayı, 10 üzeri 800 milyondu. Bu sayıyı ikinci dönemin başlangıcı kabul etti ve sistemi aynı şekilde sürdürdü. Bu süreç en sonunda 10 üzeri 80.000 trilyon gibi akıl almaz bir büyüklüğe ulaştı.
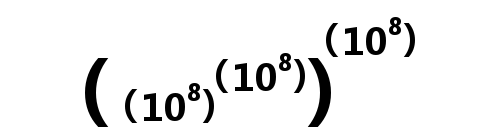
Kum sayımı için yaptığı hesaplarda ise Arşimet’in bu kadar dev sayılara ihtiyacı yoktu. Bir kum tanesinin ve evrenin büyüklüğüne dair kendi tahminlerini kullanarak, birinci dönemin yalnızca sekizinci düzenine denk gelen bir değer buldu.
Üstel gösterimle yaklaşık 8 × 10⁶³ tane Arşimet ölçüsündeki küçük kum tanesi iki ışık yılı genişliğindeki Yunan evrenini doldurmaya yetiyordu. Bu da hâlâ birinci dönemin yalnızca on ikinci düzenine karşılık gelir.
Sonuç Olarak
Arşimet, elindeki sınırlı verilere rağmen evrene dair bugün bildiklerimize en çok yaklaşan modeli sundu ve büyük sayıları tanımlamak için tamamen yeni bir yöntem geliştirdi.
Modern sayı gösterimlerinin hiçbirine sahip olmadan, büyük sayıların nasıl adlandırılacağını ve nasıl işleneceğini sistemli biçimde ele alan ilk kişiydi. On bin tabanına dayanan sistemiyle üstel ifadeyi, yani bir sayının başka bir sayının üssüne yükseltilmesini fiilen ilk kez kullanan kişi oldu. Ayrıca üslerin toplanması yasasını da keşfetti
Kaynaklar ve ileri okumalar:
- Which Is Greater, The Number Of Sand Grains On Earth Or Stars In The Sky? Kaynak site: NPR. Yayınlanma tarihi: 17 Ekim 2012. Bağlantı: Which Is Greater, The Number Of Sand Grains On. Earth Or Stars In The Sky?/
- Conselice, Christopher & Wilkinson, Aaron & Duncan, Kenneth & Mortlock, Alice. (2016). The Evolution of Galaxy Number Density at z < 8 and its Implications. The Astrophysical Journal. 830. 10.3847/0004-637X/830/2/83.
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel