Evrenin hiçbir yerinde tam bir denge yok — bu da entropinin, yani düzensizlik ve karmaşıklığın, sürekli arttığı anlamına geliyor. Boltzmann denklemi de bunu bize hatırlatıyor.

Bugün ister teknolojiden, ister bilimden ya da küresel ticaretten söz edelim; her şey giderek daha karmaşık hâle geliyor. Oysa bir zamanlar işler daha basitti. Geçmişte, çok yönlü bilginler (polymath) birden fazla alanda uzmanlaşıp her birine anlamlı katkılar yapıyordu. Ancak bugün, uzmanlaşmanın giderek derinleşmesi nedeniyle birden fazla alanda üstün başarı göstermek çok daha zor.
Bu nostaljik bir serzeniş değil, sadece gerçekçi bir tespit. Dünya eskiden daha basitti. Üstelik bu, matematiksel açıdan da geçerli. Ayrıca bu karmaşıklık yalnızca günlük hayata değil, fiziğin temellerine de yansıyor. 19. yüzyıl fizikçi ve filozofu Ludwig Boltzmann, bunu daha 1872’de fark etmişti.
Boltzmann, gazların ve sıvıların davranışlarını inceliyordu. Ondan sadece birkaç on yıl önce, maddenin temel yapı taşlarının atomlar ve moleküller olduğu fikri öne sürülmüştü. Boltzmann, bu yeni anlayışı alıp doğanın karmaşıklığını anlamak için matematiksel modellerle işledi. Bu sayede modern istatistiksel fiziğin temellerini attı.

Eğer sıvıların ve gazların nasıl davrandığını tam anlamıyla tanımlamak isteseydiniz, her bir parçacığın hareketini tek tek takip etmeniz gerekirdi. Ama Boltzmann bunun pratikte imkânsız olduğunu biliyordu. Bu yüzden, tek tek parçacıkları değil, onların ortalama davranışlarını tanımlayan bir denklem geliştirdi. Ancak bu denklem ona şaşırtıcı bir şey gösterdi: Atomlar ve moleküller tek başlarına farklı kurallara uyuyordu, bir araya geldiklerinde ise bambaşka. Yani sistem, onu oluşturan parçalardan daha karmaşıktı.
Zaman Neden Tek Yönlüdür?
Sürtünmesiz bir bilardo masasında toplar çarpışıyor ve yuvarlanıyor. Bu sahneyi videoya alıp sana izletiyorum, sonra da soruyorum: “Bu video ileri mi oynuyor, geri mi?” Net bir cevap vermek imkânsız.
Çünkü Newton’un hareket yasaları zamanın yönünü umursamaz. Toplar ileriye doğru da yuvarlansa, geri de gitse aynı kurallar geçerli olur. 19. yüzyılda fizikçiler gazların içindeki parçacıkların da böyle davrandığını düşündü: Küçük toplar gibi boşlukta hareket ediyorlar, birbirlerine çarpıyorlar ve Newton yasalarına uyuyorlar.
Ama işler o kadar basit değil. Bugün biliyoruz ki atomlar ve moleküller kuantum mekaniğine tabidir. Kuantum kuralları çok daha karmaşıktır. Yine de ilginç olan şu: Kuantum mekaniği de çoğu durumda zamanın yönünü önemsemez. Yani atom düzeyinde, olayın ileri mi geri mi olduğu fizik açısından fark yaratmaz.
Ama makroskobik düzeye —gözle görebildiğimiz dünyaya— çıktığınızda tablo değişir. Burada zamanın yönü belirleyicidir. Örneğin kahveye süt döktüğünüzü düşünün. Zamanla bu iki madde birbirine karışır ve homojen bir sıvı oluşturur. Ancak bu karışımı geriye alamazsınız. Kahveden sütü ayıramazsınız.
İşte bu çelişki Boltzmann’ı yıllarca meşgul etti. Mikro dünya ile makro dünya arasındaki bu temel fark, Boltzmann’ın en çok kafa yorduğu konuydu. Tek tek parçacıkların hareketlerini tanımlayan ve zamanı tersine çevirdiğinizde bile değişmeyen denklem sayısı saymakla bitmezken, nasıl oluyor da bu sistemler büyük ölçekte geri döndürülemez davranışlar sergiliyor? Eğer teorik olarak her çarpışma tersine çevrilebiliyorsa, neden kahveye dökülen sütü ayıramıyoruz?
Bu sorunun sezgisel bir yanıtı var: Gaz veya sıvı içindeki parçacıklar durmaksızın çarpışır. Bu çarpışmalar hızlı olanları yavaşlatır, yavaş olanları hızlandırır. Yeterince beklerseniz, sonunda sistem dengeye ulaşır. Parçacıklar ortalama olarak aynı hızda hareket eder ve uzayda eşit dağılır. Her şey zamanla homojenleşir ve bu süreci geri almak, pratikte imkânsıza yakındır.
Boltzmann denklemi karmaşık dünyayı anlamlandırır
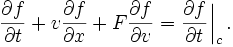
Boltzmann, parçacıkların davranışlarını açıklamak için bugün kendi adıyla anılan bir denklem geliştirdi. Boltzmann denklemi, parçacıkların hızlarının ve uzaydaki dağılımlarının zaman ve konuma göre nasıl değiştiğini tanımlar. Ayrıca, yoğunluk ya da sıcaklık gibi koşullara bağlı olarak parçacıklar arasındaki esnek çarpışmaların etkisini de hesaba katan bir “çarpışma operatörü” içerir.
Boltzmann denklemi, diferansiyel bir denklem olduğu için çözümü zordur; türevler içerir ve karmaşıktır. Ama Boltzmann, bu güçlü denklemle evrenin zamanla daha karmaşık bir hâl aldığını matematiksel olarak gösterdi.
Peki, “karmaşık” ne demek? İlk bakışta sütle karışmış bir kahve basit görünür. Ama fiziksel ve matematiksel açıdan durum tam tersidir. Çünkü aynı sıcaklık, yoğunluk ve hacme sahip bu karışım, mikroskobik düzeyde sayısız farklı parçacık düzeni içerir. Ve tüm bu farklı düzenler, makroskobik olarak aynı görünür. Yani dışarıdan bakıldığında tek bir karışım gibi görünen şeyin içinde, gerçekte sonsuz sayıda olasılık gizlidir.
Yani bir sistemin tüm büyük ölçekli (makroskobik) özelliklerini bilseniz bile, parçacıkların nerede olduğunu veya nasıl hareket ettiklerini kesin olarak söyleyemezsiniz. Çünkü aynı sonucu üreten sayısız olasılık vardır. İşte bu durum, sistemin karmaşıklığını gösterir.
Boltzmann bu karmaşıklığa “entropi” adını verdi. Bir sistemin entropisi ne kadar yüksekse, mikroskobik parçacıklarının aynı makroskobik sonucu üretme olasılıkları da o kadar fazladır. Süt ve kahve ayrı haldeyken sistemin karmaşıklığı — dolayısıyla entropisi — düşüktür. Çünkü süt molekülleri kahve moleküllerinden hâlâ ayrıdır. Fakat sıvılar karıştırıldığında, bu moleküller giderek birbirine karışır. Sistem zamanla daha karmaşık hale gelir ve entropi sürekli artar. Denge durumu sağlandığında ise entropi sabit kalır.
Sonuç Olarak
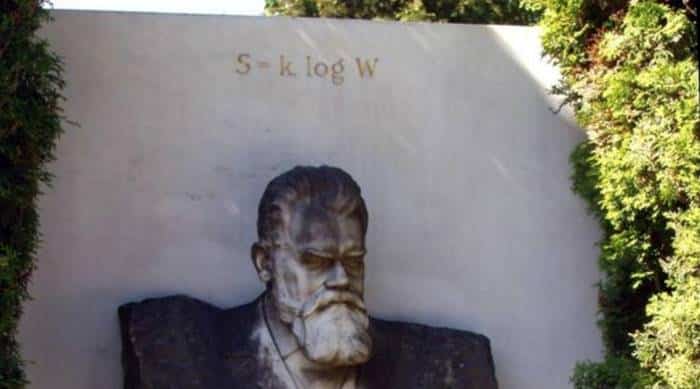
Boltzmann, bu süreci hem nitel olarak tanımladı hem de denklemiyle matematiksel olarak ispatladı. Bir sistem, dengeye yaklaştıkça karmaşıklığı — yani entropisi — kaçınılmaz biçimde artar. Entropinin matematiksel formülü Ludwig Boltzmann’ın mezar taşında yer almaktadır. Entropide olan değişiklik ΔS biçiminde gösterilirse kısa ve öz bir temsili şu şekilde olur: ΔS ≥ 0
Bu ilke yalnızca sıvılar ve gazlar için değil, evrendeki her şey için geçerlidir. Büyük ölçekte baktığımızda, hiçbir şeyin tam bir denge halinde olmadığını görürüz — hatta evrenin kendisi bile hâlâ genişlemeyi sürdürüyor. Bu durum şunu gösteriyor: Entropi, yani sistemlerin içsel karmaşıklığı, zamanla sürekli artıyor. Ve bu artış, durdurulamaz bir şekilde devam ediyor.
Kaynaklar ve ileri okumalar
Our World Is Getting More Complicated. Here’s the 19th-Century Math That Proves It. Kaynak site: Scientific American. Yayınlanma tarihi: 4 Haziran 2025. Bağlantı: Our World Is Getting More Complicated. Here’s the 19th-Century Math That Proves It
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel