Başlıkta okuduğunuz ifade doğrudur. Çıkarma işlemini gerçekten de toplama işlemi yardımıyla yapabilirsiniz. Aslına bakarsanız, bilgisayarlar bu işlemi her zaman bu şekilde yapar.

Belki duymuşsunuzdur, bilgisayarların doğrudan bildiği tek işlem toplamadır. Bu nedenle diğer işlemleri de aslında toplama yardımıyla gerçekleştirirler. Örneğin, çarpma işlemini tekrarlı toplama yoluyla yaparlar. 8 × 5 işlemini gerçekleştirmek için 8 sayısını beş kez toplarlar. Zaten çarpmanın tanımı da bu olduğu için bunda şaşırtıcı bir durum yoktur.
Aynı mantık bölme işlemi için de geçerlidir. Sonuçta, bölme işlemi ardışık çıkarma işlemleri anlamına gelir. Peki, eğer bilgisayarlar yalnızca toplama işlemi yapabiliyorsa çıkarma işlemi nasıl gerçekleşiyor? Aslında cevabı oldukça basit.
A – B işlemi için, çıkan (B) sayısının ikili sistemdeki tamamlayıcısı bulunur ve bu A sayısına eklenir. Böylece işlem yine toplama biçimine dönüştürülmüş olur. Ancak, elde edilen sonuçta en soldaki taşıma biti (1) silinir. Bu noktada akla gelen ilk soru, bir sayının tamamlayıcısının nasıl bulunacağıdır. Şimdi bunu açıklayalım.
Sayının tamamlayıcısını nasıl bulunur?
İşe önce sayının birler basamağından başlıyoruz. Sıfırları atlıyor, sıfır olmayan ilk basamağı 10’a tamamlayan rakamla değiştiriyoruz. Bu noktadan itibaren, soldaki tüm basamakları 9’a tamamlayan rakamlarla değiştirmemiz gerekiyor.
Tamamlayıcısını bulmak istediğimiz sayı 128 olsun. Önce birler basamağı olan 8 ile başlıyoruz. Bu sayıyı 10’a tamamlayan rakam 2 olduğu için, 8’in altına 2 yazıyoruz. Sola doğru devam ediyoruz. Sıradaki basamak 2’dir. 9’a tamamlayanı 7 olduğu için altına 7 yazıyoruz. Son olarak, 1 basamağını 9’a tamamlayan rakam olan 8’i yazıyoruz. İşlem bu kadar! Bu durumda, 128 sayısının tamamlayıcısı 872 olur.
Şimdi ikinci bir örnek daha inceleyelim. Bu kez tamamlayıcısını bulmak istediğimiz sayı 740. İlk olarak birler basamağı 0 olduğu için onu atlıyoruz. Sonraki basamak 4’tür. Bu sayının 10’a tamamlayanı 6’dır. Solundaki basamak olan 7’yi ise 9’a tamamlayan rakam 2’dir. Sonuç olarak, 740 sayısının tamamlayıcısı 260 olur.
Çıkarma İşlemi İle Toplama Yapalım
Artık tamamlayıcı sayının nasıl bulunacağını öğrendiğimize göre, toplama yardımıyla çıkarma işlemini nasıl yapabileceğimizi de öğrenebiliriz. Bu yöntem, özellikle çıkarma işlemini kavramakta zorlanan öğrenciler için büyük bir avantaj sağlar. Ayrıca derste bu yöntemle ilgili bir örnek vermek, konuyu daha ilgi çekici ve anlaşılır hale getirir.
Şimdi de 975’ten 740’ı, tamamlayıcı yöntemini kullanarak çıkaralım. Az önce, 740 sayısının tamamlayıcısını 260 olarak bulmuştuk. Şimdi yapmamız gereken, 975 ile 260 sayısını normal şekilde toplamaktır. Toplama işlemi sonucunda elde edilen sayının en solundaki 1 (taşıma biti) atılır. Böylece çıkarma işleminin sonucu 235 olur.

Bu yöntemi kullanırken dikkat etmeniz gereken önemli bir nokta var: Eğer çıkan sayının basamak sayısı, eksilenin basamak sayısından azsa, çıkan sayının solundaki eksik basamakları 9’larla doldurmamız gerekir. Bu durumu daha iyi anlamak için, 1267 – 138 işlemini aynı yöntemle uygulayarak açıklayalım.
Yukarıda anlattığımız yönteme göre, 138 sayısının tamamlayıcısı 9862 olur. Burada en başa 9 eklememizin sebebi, eksilen sayının (1267) dört basamaklı olmasıdır. Yani, üç basamaklı olan 138 sayısını dört basamaklı hâle getirmek için soluna bir adet 9 eklememiz gerekir.
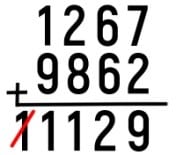
Sonuç elde etmek için şimdi 1267 + 9862 işlemini yapıyoruz. Bu işlemin sonucu 11129 olur. Ancak, tamamlayıcı yöntemde her zaman olduğu gibi en soldaki 1 (taşıma biti) atılır. Geriye kalan 1129, çıkarma işleminin doğru sonucudur.
Bilgisayarlar Tamamlayıcı Sayıyı Nasıl Buluyor?
Az önce de aktardığımız gibi, çıkarma işlemini toplama yoluyla gerçekleştirmek bilgisayarların temel çalışma prensibidir. Ancak bu, bir bilgisayar için oldukça basit bir işlemdir. Çünkü bilgisayarlar ikilik sayı sistemini (binary) kullanır; yani sayılar yalnızca 0 ve 1 basamaklarından oluşur.
Bu sistemde, bir sayının tamamlayıcısını bulmak için bilgisayar önce her bir biti tersine çevirir: 0’ları 1, 1’leri ise 0 yapar. Ardından, elde edilen sonuca 1 ekler. Böylece sayının ikili (2’lik) tabandaki tamamlayıcısı elde edilmiş olur.
Şimdi, bu işlemi bir bilgisayar gibi düşünerek örnekleyelim. İkilik tabandaki 1110010 sayısının tamamlayıcısını bulalım:
- Önce tüm bitleri tersine çeviriyoruz: 1110010 → 0001101
- Daha sonra bu sayıya 1 ekliyoruz: 0001101 + 1 = 0001110
Bilgisayarlar, bu işlemleri elektronik mantık devreleri ile çok hızlı bir şekilde gerçekleştirir. Dolayısıyla çıkarma işlemi, onlar için sadece birkaç toplama işlemi ve veri taşıma (shift etme) işleminden ibarettir. Bu tür görevler, mantık devreleriyle kolayca programlanabilir ve donanımsal olarak optimize edilebilir.
Siz de bu yöntemi kullanarak biraz alıştırma yaparsanız, çıkarma işlemlerinde hız kazanabilirsiniz. Ayrıca, diğer yazılarımızdan faydalanarak matematik bilginizi daha da geliştirebilirsiniz.
Kaynaklar ve ileri okumalar:
- Understand the mathematical trick to do subtraction by adding and its implementation in mechanical adding machines; Kaynak: Britannica. Understand the mathematical trick to do subtraction by adding and its implementation in mechanical adding machines/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






İçerilerinize bayılıyorum