Ödüllü sorular matematik dünyasında her zaman olmuştur. Ancak bunların en büyüğü 2000 yılında Clay Enstitüsü tarafından Milenyum soruları olarak belirlenmişti. Bu Milenyum problemlerin çözülmelerinin, ait oldukları alanda yeni ufuklar açacağına kesin gözüyle bakılıyor.

Milenyum soruları kapsamında yedi matematik problemi var. Enstitü, bu sorulardan herhangi birine titiz, hakemli bir çözüm sunabilecek herkese 1 milyon dolarlık bir ödül teklif etti. Rus matematikçi Grigori Perelman, problemlerden biri olan Poincaré varsayımını çözdüğü için ödüle layık görüldü. ( Grigori Perelman çözüm karşılığında kendisine verilen ödülü almadı.)
Diğer milenyum problemleri hala çözülmeyi bekliyor. Yapmamız gereken tek şey bir kağıt ve kalem alıp matematik bilgimizi kullanıp bu soruları cevaplamak. Ancak birazdan göreceğiniz gibi bunu başarmak çok da kolay değil.

Milenyum Soruları Nelerdir?
- 1- Yang-mills ve Kütle Aralığı: Çözülmedi
- 2- Riemann Hipotezi: Çözülmedi
- 3- P NP’ye karşı Problemi: Çözülmedi
- 4- Navier–Stokes Denklemleri: Çözülmedi
- 5- Hodge Kestirimi: Çözülmedi
- 6- Poincare Kestirimi: Çözüldü
- 7- Birch ve Swinnerton-Dyer Kestirimi: Çözülmedi
Riemann Hipotezi

Dünyanın en zor ve en ünlü matematik probleminin ne olduğunu belirlemek elbette tam olarak mümkün değil. Ancak, Bernhard Riemann tarafından 1859’da ortaya atıldığından beri matematikçileri şaşkına çeviren Riemann Hipotezi bunun için bir aday gibi gözüküyor.
Riemann hipotezi özünde asal sayılar daha ziyade asal sayıların sayı doğrusu üzerine dağılımı ile ilgilidir. Cevabı basit bir “evet” veya “hayır”dır, ancak bu cevaba ulaşmanın pek çok varsayımsal yolu vardır ve bunların hepsi son derece zordur.
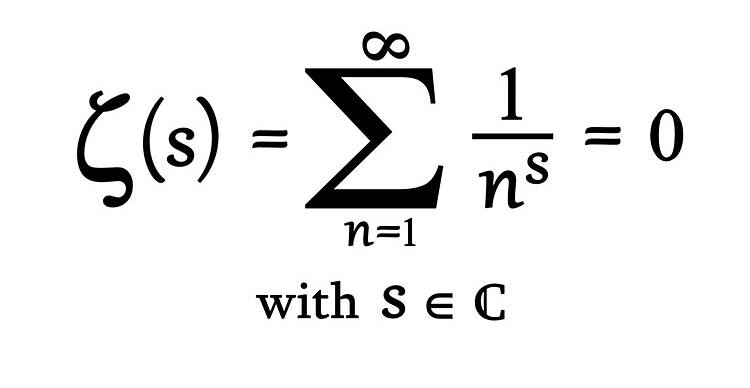
Hipotez, “Riemann zeta fonksiyonu” olarak adlandırılan matematiksel bir yapıya dayanır. Belirli bir sayıya kadar kaç asal olduğunu tahmin etmek, Riemann zeta fonksiyonunun hangi değerler için sıfır olduğunu bilmeye bağlıdır. Fonksiyonu ayrıca x= 0 ile x=1 arasındaki kritik bölgede sonsuz sayıda sıfır yapan değer vardır. Bugün Riemann hipotezi diye anılan sav bu değerlerin hepsinin karmaşık düzlemde x=1/2 doğrusu üzerinde olup olmadığıdır.
Bu milenyum problemi, asal sayılar dışında görünüşte ilgisiz alanlarda ortaya çok sık olarak çıkar. Bu nedenle, kanıtlamanın (veya çürütmenin) önemi, sayı teorisinin veya bir bütün olarak matematiğin sınırlarının çok ötesine geçer. Riemann hipotezi kanıtlanabilirse kuantum dünyasında bir çok hesaplanamayan fenomen için bize bazı yöntemler gösterecektir.
Yang – Mills Hipotezi

Kuantum dünyasının tipik özelliği dalga-parçacık ikiliğidir. Elektronlar gibi parçacıklar bazen belirli bir konuma sahip nokta parçacıklarmış gibi, bazen de sanki dalgalar gibi davranırlar. Bu tuhaf davranış, yalnızca teorik açıdan ilgi çekici değildir. Tüm elektronik cihazlarımızdaki yarı iletkenlerin davranışı, nano malzemelerin davranışı ve kuantum hesaplamanın mevcut yükselişi için temeldir.
Yang ve Mills, matematiksel yapıları kullanarak bu temel parçacıkları tanımlamak için önemli bir çerçeve sağladılar. Teori, kuantum parçacıklarının, temel parçacıkların etkileşimlerini tanımlamak için “boşluğu ile tanımlanan pozitif kütlelere sahip olduğunu öne sürüyor. Yani parçacıklar kütlesiz fotonlara benzeseler dahi sıfır kütleli olamazlar.
Kütle boşluğu, nükleer kuvvetlerin elektromanyetizma ve yerçekimine kıyasla neden son derece güçlü ve olduğunu açıklamanın da kritik bir parçasıdır. Bu özellik zaten fizikçiler tarafından deneyler yoluyla keşfedilmiş ve bilgisayar simülasyonlarıyla doğrulanmıştır. Milenyum Problemi, kütle boşluğunu açıklamak için genel bir matematik ve fizik teorisi oluşturmakla ilgilidir.
P – NP Problemi

Clay Matematik Enstitüsü, milenyum soruları için 1 milyon dolarlık ödül miktarı belirlerken, problemlerden bir tanesini küçümsemiş olabilir. Eğer matematikçiler bilgisayar biliminin “P’ye karşı NP” sorusunu doğru şekilde çözebilirse, çözümün karşılığında elde edeceklere ödül 1 milyon dolardan çok daha fazlası olacaktır.
Bilgisayarlar algoritmalarla çalışır. Ancak bazı algoritmaları gerçekleştirmek sadece mikro saniyeler alırken, bazılarını gerçekleştirmek bugünkü hızla bile milyarlarca yıl alır. Burada kilit fikir, bir algoritmanın verimliliğidir. Bu alanda çalışan araştırmacılar, bilgisayarların çeşitli türdeki problemleri ne kadar kolay çözebileceğini belirlemeye çalışırlar.
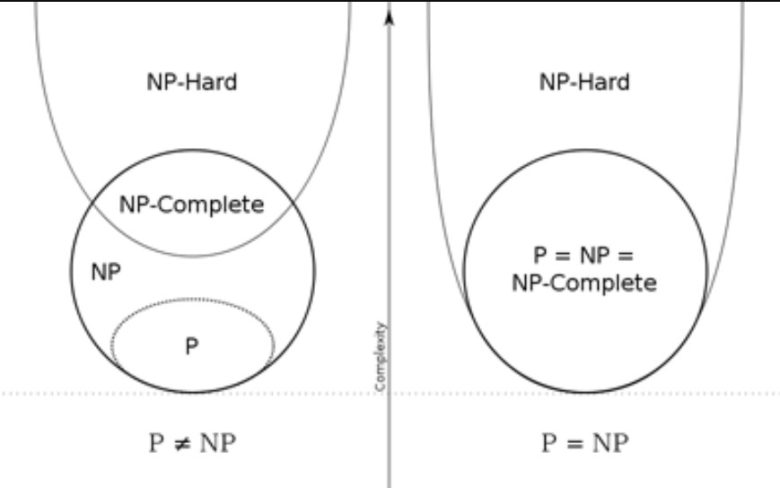
P, verimli bir şekilde çözülecek problem sınıfını temsil eder. P sınıfındaki problemlerin kolay olduğu düşünülür. Sonucunda bir bilgisayar algoritması bunları uygun bir sürede çözecektir. Ancak NP sınıfındaki problemler daha zordur. Bir bilgisayar için bile çözümü milyarlarca yıl zaman alacaktır. NP sınıfının P sınıfına eşit olması mümkündür, ancak bunun olup olmadığını kimse bilmiyor. Eğer P = NP ise o zaman tüm dijital ekonomi çökmeye karşı savunmasız hale gelir.
Navier-Stokes Denklemleri

Milenyum problemleri arasında, içinde yaşadığımız dünyaya dair anlayışımızla ilgili olan bir problem var. Bu sıvıların akışını tarif eden Navier-Stokes denklemleridir. Hava ve su en iyi bildiğimiz akışkanlardır. Nasıl hareket ettikleri ve nasıl davrandıkları bilimin doğuşundan bu yana bilim adamlarını ve matematikçileri büyülemiştir.
Navier-Stokes denklemleri, kısmi diferansiyel denklemler kümesidir. Bu denklemler hızdaki değişiklikleri, basınçtaki değişiklikleri ve sıvının viskozitesini ilişkilendirir. Newton’un İkinci Yasası, akışkan hızının değişim oranlarını akışkana etki eden kuvvetlerle ilişkilendiren bir diferansiyel denklem sistemi üretir.
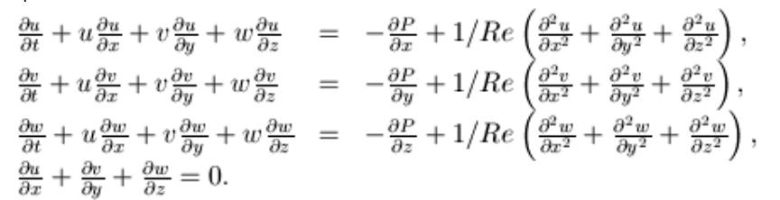
Aslında Clay Enstitüsü’nün ödülü vermek için talep ettiği bilgi ise oldukça basittir. Birincisi denklemlerin çözümlerinin varlığına odaklanır. İkincisi ise bu çözümlerin sınırlı olup olmadığını (sonlu kalıp kalmadığını) sorar. 200 yıldır süregelen deneyler sonucu anladık ki bu denklemler kesinlikle işimize yarıyor. Navier-Stokes’un öngördüğü akışlar, deneylerde gözlemlenen akışlara uyuyor. Ancak sizin de tahmin edebileceğiniz gibi bu denklemleri çözmek çok da kolay değil.
Hodge Varsayımı

Hodge Varsayımı Milenyum soruları arasında açıklanması en zor olanlardan biridir. Basitleştirmek gerekirse, problem karmaşık matematiksel şekillerin basit olanlardan oluşturulup oluşturulamayacağını sormaktadır. Problemi legolardan yeni şekiller oluşturmak gibi düşünebilirsiniz. Ancak temel fikir, boyutları artan basit geometrik yapı taşlarının birbirine yapıştırılmasıyla belirli bir nesnenin şekline ne ölçüde yaklaşılabileceğini bilmektir.
Hodge varsayımını 1950’de yaptı ve geometrinin gelişimindeki öncülerin çoğu bu temel tanıma problemi üzerinde çalıştı. Bu nedenle günümüzde matematikçiler çeşitli nesneleri incelemede ilerlemeler sağladı. Cebirsel geometri dalında matematikçiler, sayıların ilişkilerini ve simetrisini inceleyen soyut cebirle, çeşitli uzaylarda biçimleri inceleyen geometriyi birleştirmeye uğraşır. Hodge çemberleri, cebirsel ağırlık taşıyan, ama görünür bir geometrik yorumu olmayan yapılardır.
Cebirsel çemberlerinse geometrik yorumları var, çünkü bunlar uzayda kesişen eğrilerle ilgilidir. Ama bunlar da cebirsel olarak fazla güçlü değillerdir. Hodge varsayımı, bu ikisini birleştiriyor. Bir Hodge çemberinin, cebirsel çemberlerin bir toplamı olarak yazılabileceğini söylüyor. Clay Matematik Enstitüsü, Hodge varsayımını yeni yöntem ve teknolojilerin kapsamlı gelişimini teşvik etme kapasitesine sahip bir problem olarak düşünüyor. Bu nedenle de onu Milenyum sorularından biri olarak seçkisine dahil etmişti.
Birch ve Swinnerton-Dyer Varsayımı

Eliptik eğriler olarak bilinen E: y 2 = x 3 + a x + b biçimindeki denklemlerin antik çağlara kadar uzanan uzun ve seçkin bir geçmişi vardır. Burada a ve b sabit rasyonel sayılardır. Ayrıca E eğrisinin düzgün olmasını sağlamak için, onun diskriminantının 4a3 + 27b2‘nin sıfır olmadığını da varsaymak gerekir.
Bu eğriler, başta sayılar teorisi olmak üzere modern matematiğin birçok dalında karşımıza çıkarlar. Ancak eliptik eğrilerin elipslerle hiçbir ilgisi yoktur. Bu eğrilerin bir örneğini aşağıda görebilirsiniz.
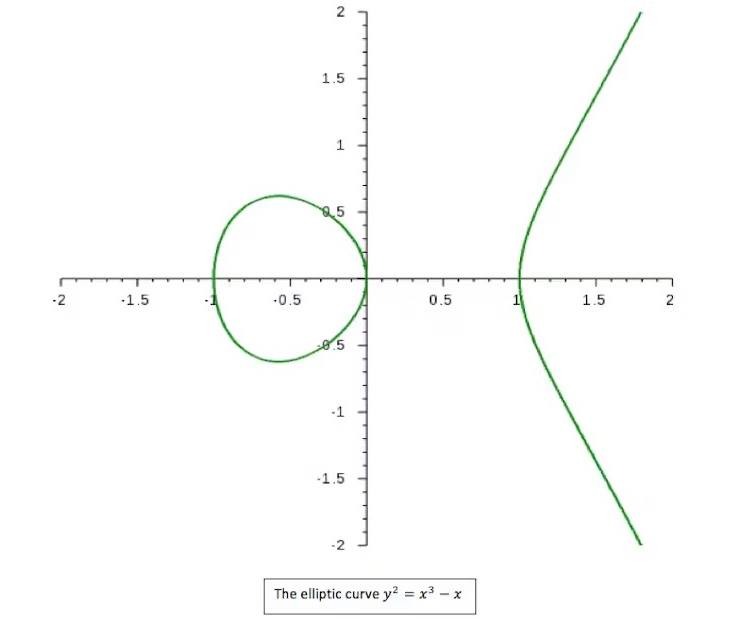
Antik Yunan matematikçi Diophantus en önemli matematik çalışması olan Arithmetica isimli kitapta polinom denklemlerinin çözümlerini incelemişti. Diophantus’un ele aldığı ana sorunlardan biri, belirli bir polinom denkleminin tüm çözümlerini bulmaktı. İkinci derece denklemler için bu problemin tam bir cevabına sahibiz.
Şimdiki amacımız E’yi tanımlayan denklemi sağlayan tüm rasyonel çözümleri (x,y) bulmaktır. Her eliptik eğri ile bağlantılı, “L-fonksiyonu” denen matematiksel bir varlık vardır. Varsayım, yalnızca belirli bir değerde L-fonksiyonunun sıfır olması halinde bir eğri üzerinde sonsuz sayıda rasyonel nokta bulunacağını söylüyor. Problem soyut gelmiş olabilir. Ancak Andrew Wiles’ın Fermat’nın Son Teoremi’ni kanıtlamak için kullandığı matematikle aynı alanı paylaşıyor.
Kaynaklar ve ileri okumalar:
- An eminent mathematician claims to have solved one of math’s greatest mysteries. And it’s one of 6 problems with a $1 million prize. Yayınlanma tarihi: 25 Temmuz 2018. Kaynak site: Business Insider. Bağlantı: An eminent mathematician claims to have solved one of math’s greatest mysteries. And it’s one of 6 problems with a $1 million prize.
- How Numbers Work; Discover the strange and beautiful world of mathematics; New Scientist Books
Matematiksel