Satranç oynamayı sever misiniz? O zaman sekiz vezir bulmacası hakkında bir biçimde bilginiz vardır. Duymadıysanız klasik bir satranç bulmacası ile sizi tanıştıralım.

Bu sorunun adı yabancı kaynaklarda Eight Queens Puzzle Türkçede Sekiz Vezir Bulmacası olarak bilinmektedir. İlk olarak 1848 yılında gündeme gelen problem aslında 8×8’lik bir satranç tahtasına 8 adet veziri birbirlerine saldıramayacakları şekilde yerleştirmek ile ilgilidir. Bulmaca, başka bir deyişle, iki vezirin aynı satırı, sütunu veya köşegeni paylaşmamasını gerektiğini ortaya koyar
Satrancın kurallarını biliyorsanız vezirin satranç tahtası üzerinde en güçlü taş olduğunu biliyorsunuzdur. Zira her yöne doğru sınırsız bir hareket özgürlüğüne sahiptir. Bulmacanın doksan iki farklı çözümü vardır, ancak döndürmeler ve yansımalar hesaba katılırsa, 12 benzersiz çözüm ortaya çıkar.
Sekiz Vezir Bulmacası Çözümü
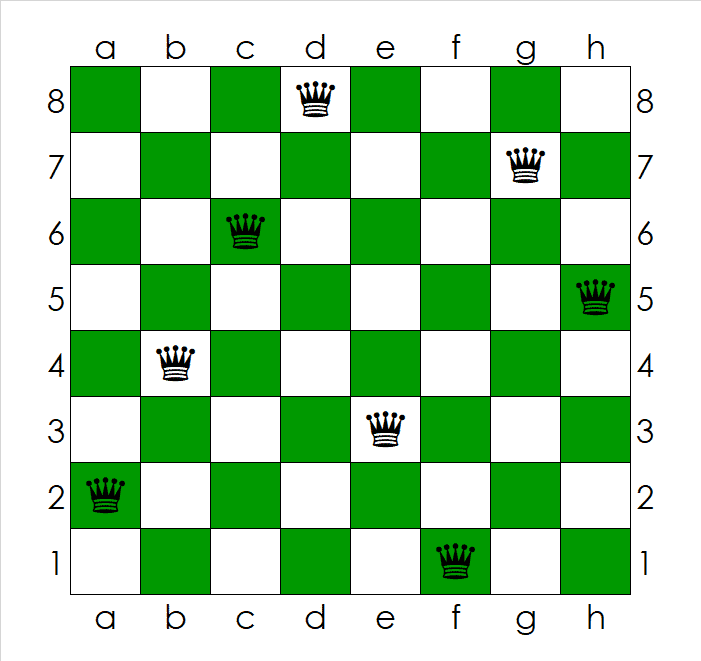
Vezirlerin konumlarını {k1, k2, … k8} biçiminde gösterirsek genel çözüm şu şekilde olur. Bir vezir ilk sütunun k1’inci karesinde, diğeri ikinci sütunun k2’nci karesinde vb. olacaktır. On iki çözüm artık karşılık gelen sayılarla temsil edilebilir; örneğin, 41582736’daki sayısındaki rakamların her biri, soldan sağa sütunlarda alttan kn konumunu temsil eder.
Yani “4”, birinci sütunun altından dördüncü konumdaki bir vezir anlamına gelir; “1” ikinci sütunda en alt konumdaki vezir anlamına gelir; “5” üçüncü sütunun en altından beşinci pozisyondaki veziri temsil eder ve bu böyle devam eder. Bu durumda 12 olası çözüm aşağıdaki gibi olur.

Karl Friedrich Gauss, 1859’da bu bulmacayla ilgilenmeye başladı ve 72 çözüm olduğu sonucuna vardı. Bulmacayı çözmek için kullandığı deneme-yanılma yönteminden memnun olmayınca da soruyu bir aritmetik problemine dönüştürdü.
Gauss’un Çözümü Nasıldı?
Bunu nasıl başardığını görmek için yukarıdaki 41582736 sayısını ele alalım. Aslında uyguladığı yöntem Gauss’un hayat hikayesini bilenlere tanıdık gelecektir. Önce sayıyı yazdı daha sonra sayıdaki her rakamın altına kaçıncı sütunda bulunduğunu yazdı ve topladı.
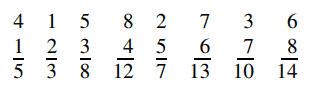
Sonra da bir ters çevirme hilesi yaparak yeni bir toplam elde etti.
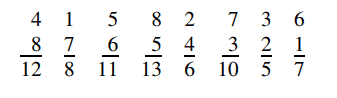
Her bir sütun için çıkan sonuçların farklı olup olmadığını kontrol etti. Birbiri ile aynı çıksaydı o dizilim sekiz vezir bulmacasının çözümü olamayacaktı. Ancak birbirinden farklı çıkanlar çözüm olabilirdi. Örneğimizde gördüğünüz gibi her bir sütunun sonucu birbirinden farklı ve bu bulmacanın çözümlerinden birisidir.
Ödül Bu Sorunun Neresinde?
Görünüşte basit olan bu bulmaca, genellemede teorik bir zorluk ortaya çıkarır. Ancak çözülürse de önemli teorik sonuçlar üretebilir. Aynı koşullarda, 20 adet veziri 20×20’lik bir tahta üzerine, ya da 100 adet veziri 100 x 100’lük bir tahta üzerine yerleştirmek durumunda kaldınız diyelim. Bu sorunun “n-Queen’s Puzzle” dilimize çevirir isek n Vezir Problemi olarak adlandırılan bu biçimidir.

Ve n (n=sıra, sütun ve vezir sayısı) büyüdükçe işler gerçekten karışır. Bunun sonucunda da soruyu çözmekte son derece güçlü bilgisayarlar bile aciz kalır. Ancak bu sorunun yine de çözülmesi mümkündür. O zaman bir şart daha ekleyelim. Problemin bir versiyonunda bazı vezirler önceden yerleştirilmiş durumdadır. Ve bunları hiç hareket ettirmeden diğerlerinin yerleştirilmesi gerekmektedir.
Ve bu soruyu çözen bir bilgisayar programı yazılırsa, bu çözüm bizi başka soruların çözümüne götürebilir. Çünkü bu soru aslında bir P – NP sorusu. Bu da soruyu çözen herhangi bir algoritmanın, NP sınıfındaki herhangi bir soruyu çözmek için dolaylı olarak kullanılabileceği anlamına geliyor.
P=NP bir Milenyum Ödüllü bulmaca olduğu için bu soruyu çözebilen, o soruyu da çözmüş sayılacak ve 1 milyon dolarlık bir ödül kazanacak. Bu arada hatırlatalım bu sorunun ilk versiyonu yani n Vezir Problemi bir P=NP sorusu olarak kabul edilmiyor.
Vezir Problemi Kısmen Bir Matematikçi Tarafından Çözüldü

Sonucunda bir ödül olmasa da n-Vezir Problemi uzun zamandır çözümsüz bekleyen bir problem idi. Bu problem yakın zamanda Harvard Üniversitesinden Dr. Michael Simkin tarafından çözüldü. Dr. Simkin, çok sayıda vezirin büyük satranç tahtalarına hiçbir birbirine saldırmadan yaklaşık olarak (0,143n)n farklı şekilde dizilebileceğini kanıtladı.
Simkin’in bu çözümü bize kesin cevabı sağlamıyor. Ancak yaklaşık 150 yıllık bu problemde bize bir alt ve üst sınır sağlamasa açısından önem taşıyor. Problem üzerinde beş yıl çalışan Dr. Simkin, sonuca her yeni vezir satranç tahtasına yerleştirildikten sonra saldırı altında olmayan boş karelerin sayısını izleyerek ulaştığını söylüyor.
Kaynaklar ve ileri okumalar:
- The 8-Queens Puzzle; Bağlantı: https://en.wikipedia.org/
- Marcel Danesi; Ahmes’ Legacy; Puzzles and the Mathematical Mind; Springer International Publishing
- Harvard mathematician largely resolves 150-year-old chess problem involving most powerful piece on board; yayınlanma tarihi: 21 Ocak 2022; Bağlantı: Harvard mathematician largely resolves 150-year-old chess problem involving most powerful piece on board/
- Sacaluga, David. (2021). An alternative algorithm for the n –Queens puzzle. Recreational Mathematics Magazine. 8. 39-73. 10.2478/rmm-2021-0003.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel