Hesaplamalı sinirbilim (aynı zamanda matematiksel sinirbilim olarak da bilinir), matematiksel modelleri, teorik analizleri ve soyutlamalarını kullanarak beynin gelişimini, yapısını, fizyolojisini ve bilişsel yeteneklerini yöneten ilkeleri anlamak için kullanılan bir sinirbilim dalıdır. Bir anlamda sinirbilim, deneysel olarak gözlemlenen davranışlara açıklık getirmek için matematiği anahtar olarak kullanır. Detaylara geçmeden önce biraz bilgilerimizi tazeleyelim.
Sinir Hücrelerimiz Nasıl Çalışır?
Herhangi bir biyoloji ders kitabını açtığınızda hiç şüphesiz “Merkezi Sinir Sistemi” veya “İnsan Beyni” adlı bir bölüm göreceksiniz. Satırlarda şöyle yazar: “Nöronlar diğer adıyla sinir hücreleri, sinir sisteminin ana bileşenleridir. Duyu organlarından elektrik sinyalleri şeklinde bilgi gönderip alırlar, beyinle iletişimi kolaylaştırırlar.” Metin muhtemelen her insan beyninde 86 milyardan fazla nöron olduğundan da bahseder. Bununla birlikte, kitap muhtemelen nöronların bu elektrik sinyalleri üretme sürecini gerçekte nasıl gerçekleştirdiğini açıklamaz.
Bir nöron her normal hücre gibi, bir gövdeye ve onun için de bir çekirdeğe sahiptir. Fakat benzerlik bundan öteye gitmez. Hücrenin bir tarafı uzun ince bir tel gibi uzanır. Diğer tarafı ise parmak benzeri uzantılar taşır. “Akson” adı verilen uzun ince tel elekriksel atımları başka sinir hücrelerine iletirken, “dendrit” adı verilen uzantılar diğer sinir hücrelerinin aksanlarından elektrik sinyallerini alır. Aşağıda bir nöronun anatomisini görebilirsiniz.
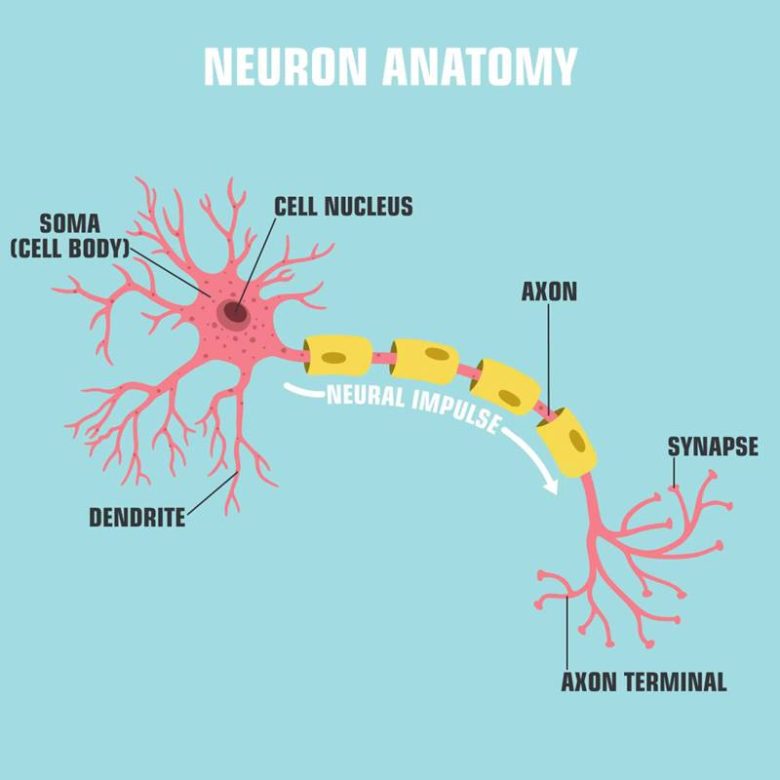
Nöronlar, bilgi taşıma gibi kritik bir görevi üç adımda gerçekleştirir. İlk olarak, duyu organlarından sinyal veya bilgi almaları gerekir. Ardından, alınan verilerin iletilmesine gerek olup olmadığına karar verirler. Son olarak, sonraki hareket tarzını hedef hücrelere veya diğer nöronlara iletirler. Buradaki ana soru şudur. Bu iletişim nasıl gerçekleşir?
Nöronlarda Elektrik Nasıl Üretilir?
Sinir hücreleri, hem elektriksel hem de kimyasal sinyalleri kullanarak bilgi aktarır. Elektrik sinyalleri sinir hücreleri içinde bilgi taşımak için kullanılırken, kimyasal sinyaller iki komşu nöron arasında bilgi aktarmak için kullanılır. Dendritler ve soma, gelen tüm bilgilerin alınmasından ve işlenmesinden sorumludur.
Dendritler üzerinde, diğer nöronlardan sinyal almak için reseptörler vardır. Bu sinyaller, nörotransmiterler adı verilen kimyasal bir madde şeklinde gelir. Gelen sinyalin tipine bağlı olarak, nöron ya uyarılır ve elektriksel darbeler üretir ya da ateşlenmesi engellenir. Bilgi işlendikten sonra, soma nöronun bir sonraki parçası olan aksona bir yanıt gönderir.
Burada önemli bir nokta, bir sinir hücresinin aksonunun bir diğerinin dendritine değmemesidir. Arada “sinaps” adı verilen bir boşluk vardır. Aksondan gelen elektrik sinyali burada kimyasal habercilere dönüşür. Bu haberciler aradaki boşlukta yayılarak reseptörlere kenetlenir. Reseptörler ise iyon kanallarını açarak yeni bir elektrik sinyalini tetikler. Sinir hücreleri diğer sinir hücreleriyle bir ağ da oluşturabilir. Bu durumda her bir sinir hücresi, dendritleri aracılığıyla birçok başka hücrenin aksonlarına bağlanır. Böyle bir ağ, karmaşık davranışlar sergileme potansiyeline sahiptir. Sinir hücrelerinin özetle nasıl çalıştığını anladıysak matematiksel sinirbilim konusunda geri dönebiliriz.
Sinir Hücrelerinin İşlevlerini Matematik Yardımıyla Nasıl Anlayabiliriz?
Sinirbilimcilerin temel amacı, organizmanın duyusal bilgiyi nasıl aldığını, bu bilgilerin beyinde nasıl entegre edildiğini ve kullanıldığını ve bu tür işlemlerin çıktısının organizma tarafından nasıl anlamlı kararlar ve davranışlarla sonuçlandığının anlaşılmasını sağlamaktır. Hesaplamalı sinirbilim, beyin işlevini simüle etmek ve modellemek için bilgisayarları kullanarak beynin nasıl hesapladığını anlamaya çalışacak model ve öneriler sunar.

Bu alanda çalışanlar beynin biyolojik işlevlerine dayalı olarak veri toplar ve bilgisayar modelleri oluştururlar. Diğer bilim insanları da biyolojik veya psikolojik uygulamaları olup olmadığını görmek için bu modelleri test eder. Hesaplamalı sinirbilim, sinirbilimin en hızlı büyüyen alt alanlarından biridir. Tüm çalışmaların amacı daha gerçekçi bir sinir ağı modeli geliştirmek, geliştirilen modelin biyolojik sinir hücrelerinin yapısına benzerliğinin artmasını sağlamaktır.
Ayrıca Göz Atmak İsterseniz…
Kaynaklar ve ileri okumalar:
- Neurons, Synapses, Action Potentials, and Neurotransmission; Yayınlandığı Yer: Illinois State University; Bağlantı: https://mind.ilstu.edu/
- A Brief Introduction to Computational Neuroscience Part 1; https://towardsdatascience.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





