
İmkansızı düşündüğünüzde, aklınıza ne geliyor? Elbette bu soruya bir çok cevap verebilirsiniz. Örneğin bir denizaltında pencereleri açmanız imkansızdır. Yıllar önce insanlar, bir insanın uçmasının imkansız olduğunu düşünüyordu. Aynı biçimde adil bir oylama sistemin de imkansız olduğunu söylenir.
Bu tam olarak Kenneth Arrow adlı bir araştırmacının Arrow’un İmkansızlık Teoremi ile göstermeye çalıştığı şeydir. ‘Arrow’s Paradox’ olarak da adlandırılan teorem, adil oylama ilkelerine bağlı kalarak, bir seçimde tercihli bir sonuç elde etmenin mümkün olmadığını belirtir.
Bu noktada Kenneth Arrow’u yanlış anlamamak önemlidir. Kendisi oy vermenin adil bir yolu olmadığından bahsetmemektedir. Tercihli oylamanın ideal bir yolu olmadığını bizlere göstermeye çalışır. Tercihli oylama, seçmenlerin yalnızca en çok tercih edilen adayı seçmek yerine her adayı tercih sırasına göre sıralamasına izin veren bir oylama yöntemidir.

Diyelim ki arkadaşlarınızı akşam yemeğine çağırdınız ve ardından da tatlı servisi yapmadan önce adil olmak adına tercihlerini en çoktan en aza sıralamalarını istediğiniz. Menünüzde bulunan pasta, dondurma ve kurabiye seçenekleri arasında her misafiriniz bir tercih sıralaması yaptı. Siz de en çok tercih edilene bakarak servisi yaptınız.
İşte Arrow bu tercihli sıralama da sorunlar olduğunu bizlere aktarır. Sonuçta er yada geç bir çıkmazla karşılaşacağınızı söyler.
Seçim Sistemlerindeki Sorun Nedir?
Detaylara geçmeden önce seçim sistemleri ve matematik arasındaki ilişkiyi anlamaya çalışalım. Demokraside yeni bir hükümet kurma zamanı geldiğinde seçim yapılır. Bunun içinde halk oy kullanmak için sandık başına gider.
Milyonlarca oy pusulası daha sonra bir sonraki seçilmiş yetkilinin kim olduğunu belirlemek için sayılır. Ancak her tür oylama sistemi, adaletini sorgulanabilir kılan sorunlarla karşılaşır.

Aslında çoğumuzun aklına seçim dediğimiz zaman oyumuzu kullanmak ve en çok oyu alan kişinin seçimi kazanması gelse de matematikçiler uzun süre adil bir seçim sistemi bulmak için de çabaladılar.
Konuyu daha iyi açıklamak adına bir örnek verelim. 100 kişinin katıldığı bir seçimde Ali 40, Ahmet 35, Ayşe 25 oy aldı diyelim. Bu durumda Ali seçimi kazanmıştır. Ancak öte tarafta da unutmayalım ki 100 kişiden 60 kişi de Ali’ye oy vermedi. Yani bu sonuç yeterince adil değildir.
Günümüzden çok daha önce, Marquis de Condorcet (1743-1794) isimli bir Fransız matematikçi çoğunluk tarafından karar verme kriterini benimsemenin doğasında var olan zorluğu bizlere göstermişti. ( Detaylar için: Seçimin Kazananı Neden Belirlenemez? Condorcet Yani Seçim Paradoksu?
Buna karşılık matematikçi Jean-Charles de Borda (1733–1799) başka bir seçim yöntemi önerecekti. Aslında Borda yöntemi adayların seçmenlerin tercihlerine göre sıralanması gereken birçok durumda halen kullanılmaktadır.
Daha iyi veya daha adil bir sistem bulma girişimleri, 1951’de Stanford Üniversitesi’nden bir ekonomist olan Kenneth Arrow, toplam tercihler konusuna şaşırtıcı yeni bir ışık tutan bir sonuç sunana kadar yıllarca devam etti.
Oylama Paradoksu Diğer Adıyla Arrow İmkansızlık Teoremi Nedir?
Mükemmel bir oylama sistemi var mı? 1950’lerde ekonomist Kenneth Arrow kendine bu soruyu sordu. Arrow aksiyomatik yaklaşımı seçti. Gerçek seçim sistemlerini önermek ve analiz etmek yerine, yerine getirilmesi gereken bir dizi makul kriter ortaya koydu. Bu kriterlerin minimalist bir listesi aşağıda gördüğünüz gibidir.
- Alakasız alternatiflerin bağımsızlığı: Adaylardan biri çekilirse ve bu, seçmenlerden herhangi birinin kalan adaylarla ilgili puanını etkilemiyorsa, sistemin kalan adaylara verdiği puan da değişmez.
- Oybirliği: Grubun tüm üyeleri A adayını B adayına tercih ediyorsa, sistemin verdiği grup sıralaması da A’yı B’ye tercih etmelidir.
- Diktatör yok: Diktatörlerin olmaması gerekir. Seçmenlerin tercihleri herhangi bir biçimde etkilenmemelidir.
- Tercihler “geçişli” olmalıdır. Yani A’yı B’ye ve B’yi C’ye tercih ediyorsanız, A’yı aynı zamanda C’ye de tercih etmelisiniz. Bu senaryoda, açıklanamayan bir nedenle C’yi A’dan daha çok tercih ediyorsanız bu tercihler “geçişsiz” hale gelir.

Arrow, üç veya daha fazla aday ve iki veya daha fazla seçmen varsa, seçmenlerin tercih sıralamalarını girdi olarak alarak çalışan ve çıktı olarak tek bir sıralama döndüren hiçbir oylama sisteminin bu koşulları karşılayamayacağını matematiksel olarak kanıtladı.

Harvard Üniversitesi ve Stanford Üniversitesi’nde uzun bir öğretmenlik kariyerine sahip olan Arrow, A Difficulty in the Concept of Social Welfare başlığı ile sonuçlarını doktora tezinde tanıttı. Arrow’un İmkansızlık Teoremi adı verilen bulgusu ona 1972’de İktisadi Bilimlerde Nobel Ödülünü kazandırdı.
Matematiksel olarak ispatı hiç de zor olmayan sonuç, sosyal bilimciler üzerinde büyük etki yarattı. Matematik, başarılabileceklerin sınırlarını çizdi. Arrow’un teoremi, hiçbir oylama sisteminin tüm aksiyomlara uyamayacağını ortaya koydu. Başka bir deyişle, hangi oylama sistemi seçilirse seçilsin, aksiyomlardan biri er yada geç ihlal edilecekti.
Arrow İmkansızlık Teoremi İçin Bir Örnek
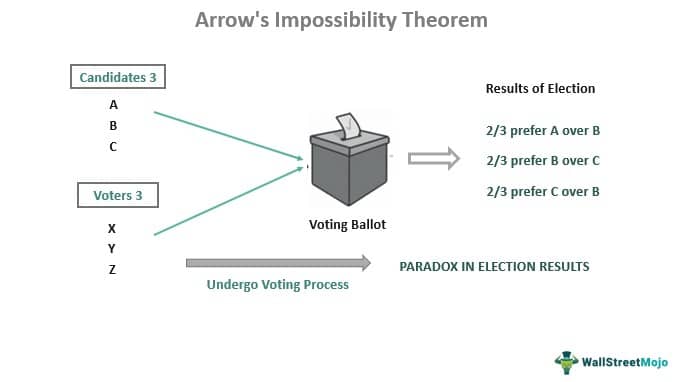
Diyelim ki üç projenin oylanması gerekiyor. Bu projeler bir kere daha A; B; ve C biçiminde olsun. Oy kullanacak 99 kişi var. Oylama yapıldı ve sonuçların aşağıdaki gibi olduğu görüldü.
- A > B > C (1/3’ü A’yı B’ye ve yine 1/3’ü B’yi C’ye tercih eder)…..33 oy
- B > C > A (1/3’ü B’yi C’ye ve yine 1/3’ü C’yi A’ya tercih eder)…..33 oy
- C > A > B (1/3’ü C’yi A’ya ve yine 1/3’ü A’yı B’ye tercih eder)…..33 oy
Bu durumda;
- 66 seçmen A’yı B’ye tercih ediyor
- 66 seçmen B’yi C’ye tercih ediyor
- 66 seçmen C’yi A’ya tercih ediyor
Dolayısıyla seçmenlerin üçte iki çoğunluğu A’yı B’ye; B’yi C’ye ve C’yi A’ya tercih ediyor. Gördüğünüz gibi ortaya bir paradoksal sonuç çıktı.
Seçim yöntemleri üzerine yapılan araştırmaların günlük yaşam üzerinde bir etkisi oldu mu? Çok değil. Birkaç örnekte, özellikle politika yapıcıların uzmanlara danışma zahmetine katlandıkları durumlarda, tercih edilen yöntemlerin sınırlamalarının dikkate alındığının görülebildiği doğrudur. Ancak çoğu durumda bu böyle değildir.
Ancak yine de bu bulguların önemli bir karşılığı da oldu. Sonucunda Condorcet ve Arrow bize oylama sistemlerinin düşündüğümüzden daha karmaşık olduğunu ve oylama sistemlerini matematiksel olarak nasıl analiz edeceğimizi gösterdiler.
Kaynaklar ve ileri okumalar:
- Arrow’s Impossibility Theorem Definition; yayınlanma tarihi: 28 Aralık 2020; Bağlantı: https://www.investopedia.com/
- Maths in a minute: Arrow’s theorem; yayınlanma tarihi: 29 Mayıs 2013; Bağlantı: https://plus.maths.org/contentt
- Arrow’s Impossibility Theorem: Can We Really Have A ‘Fair’ Voting System?; yayınlanma tarihi: Bağlantı: https://www.scienceabc.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









