Sonsuzluğu Bilen Srinivasa Ramanujan Ve Günümüze Mirası

Matematik tarihi boyunca Srinivasa Ramanujan’a uzaktan yakından benzeyen hiç kimse olmadı. Belki de bu nedenle hakkında uzun metrajlı bir film çekilen ender matematikçilerden biri oldu.

Robert Kanigel tarafından kaleme alınan daha sonra da beyaz perdeye aktarılan The Man Who Knew Infinity ( Sonsuzluğu Bilen Adam) bu parlak matematikçi ile bizlerin tanışmasına neden oldu. Onun yaşam öyküsünün bize kadar ulaşmasındaki en önemli faktör ise elbette matematikçi G.H. Hardy ve yazdığı kitaplardı.

Srinivasa Ramanujan, 22 Aralık 1887’de, Hindistan’ın Tamil Nadu kentinde doğmuş ve Hindistan’ın Kumbakonam kasabasında, bugün başarılarını simgeleştirmek için bir müzeye dönüştürülen bir evde büyümüştü. Yoksulluk ile mücadele eden ailesi ona ancak temel bir eğitim imkanı sunabilmişti. Ancak o yine de henüz 11 yaşındayken üniversite düzeyinde matematik bilgisine sahipti ve matematik teoremleri geliştirmeye başlamıştı.

Başlangıçta Ramanujan Hindistan’ın Madras kentinde tek başına çalışıyor, kitaplardan kendi kendine öğreniyor ve ilhamını Hindu tanrıçası Namagiri’ye atfediyordu. Aralık 1903’te, 16 yaşındayken Madras Üniversitesi’nin giriş sınavını geçti. Ancak diğer tüm dersleri hariç tutarak matematiğe yoğunlaştığından ikinci yıldan sonra ilerleme kaydedemedi. 

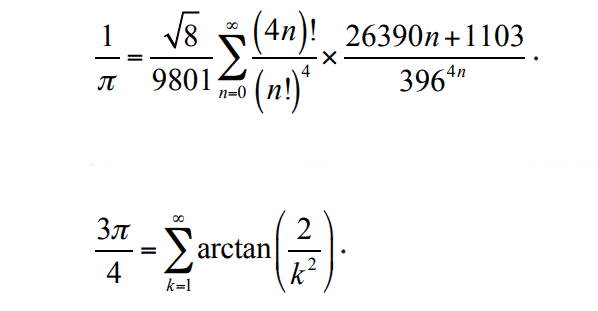
1909’da, annesi tarafından seçilen ve o sırada sadece on yaşında olan bir kızla evlendi. Bu bir Hint geleneğiydi ve sıra dışı değildi. Şimdi aile sorumlulukları olan Ramanujan bir iş, özellikle de bir büro görevi arıyordu. Bir süre ders vererek kendini idame ettirdi. Sonunda, Mayıs 1913’te Madras Üniversitesi’nde bir iş buldu ve ailesiyle Triplicane’ye taşındı. Bu süre boyunca Ramanujan matematiğe olan tutkusunu sürdürdü ve sürekli kesirler, ıraksak seriler, eliptik integraller, hipergeometrik seriler ve asal sayıların dağılımı üzerinde çalışmaya devam etti.

Ramanujan’ın Hayatını Değiştiren Kitap

1903’te, Srinivasa Ramanujan on altı yaşındayken Synopsis of Elementary Results in Pure and Applied Mathematics (Soyut ve Uygulamalı Matema­tikte Temel Bilgiler Özeti) adındaki bir kitaba denk geldi. Kitap aslında bir ders kitabıydı ve ispatlara girilmeden binlerce sonuç, formül ve denklem içeriyordu. Kuramsal matematiği ilk kez bu kitaptan öğrenen Ramanujan’a hayatı boyunca belki de bu nedenle bir ispat yapma ihtiyacı duymadı.

1911’e gelindiğinde Ramanujan, önde gelen matematikçilerin, özellikle de İngiltere’dekilerin takdirini kazanması gerekiyordu. Bu nedenle 1913’ün başlarında, Cambridge’deki ünlü İngiliz matematikçi GH Hardy’ye, keşiflerinin uzun bir listesini içeren bir mektup gönderdi. Bu mektup, her ikisinin de hayatını değiştirecekti.

Ramanujan’ın mektubunu aldığında henüz 36 yaşında olmasına rağmen Hardy, İngiltere’nin önde gelen matematikçisiydi. Kendisi bir diğer önemli matematikçi olan J.E. Littlewood ile eşi benzeri olmayan efsanevi bir ortaklık kurmuş ve 100’den fazla ortak makale yazmıştı. Bu sayede İngiltere’yi matematikte, özellikle sayılar teorisi ve analizinde bir süper güce dönüştürmede etkili olmuşlardı.

Hardy sadece olağanüstü bir matematikçi değildi, aynı zamanda yetenekli öğrencileri yetiştirmeye istekli harika bir öğretmendi. Sonunda Hardy, Ramanujan’a cesaret verici bir yanıt gönderdi. İkili bir süre diyaloglarına mektuplar üzerinden devam ettiler.

Hardy için Ramanujan’ın tamamen istisnai olduğu açıktı; ancak Ramanujan profesyonel bir matematikçinin temel araçlarından yoksundu. Hardy, Ramanujan’ın potansiyelini ortaya çıkarması için sağlam bir temele sahip olması gerektiğini biliyordu. Sonunda Ramanujan, İngiltere’ye doğru yola çıktı ve Nisan 1914’te Cambridge’e vardı.

Srinivasa Ramanujan’ın Hardy İle Buluşması

Neredeyse üç yıl boyunca işler son derece iyi gitti. 1916’da Ramanujan Cambridge’den lisans derecesini aldı. Hardy’nin büyük yardımıyla, birbiri ardına mükemmel makaleler yayınladı. Kısa bir süre sonra da Royal Society of London’ın bir üyesi seçilerek hayatının en büyük onurunu elde etti.

Ancak 1917 baharında Ramanujan hastalanacak ve sonrasında da bir türlü tam olarak iyileşemeyecekti. Ne yazık ki Ramanujan 26 Nisan 1920’de henüz 32 yaşındayken hayatını kaybetti. Ramanujan’ın gücünün zirvesindeyken ölümü matematiğe büyük bir darbe indirdi. Onun benzeri bugüne kadar bir daha karşımıza çıkmadı. Hardy ile Ramanujan’ın kurduğu türden bir ortaklığa da bir daha rastlanmadı. Hindistan hükümeti, olağanüstü başarılarını onurlandırmak için, Ramanujan’ın 22 Aralık olan doğum gününü, Ulusal Matematik Günü olarak kabul etti.

Srinivasa Ramanujan’ın Günümüze Mirası

Hardy ve Ramanujan, pozitif tam sayılarla çalışırken ilk bakışta ilgisiz gibi gözüken matematiksel bileşenleri kullanarak tamamen yeni bir yaklaşım geliştirdiler. Ramanujan’ın kalıpları görme konusunda olağanüstü bir yeteneği vardı. Sonuçlarını nadiren kanıtlasa da, toplamlar ve integrallerle ilgili bir dizi değerlendirme bıraktı. Özellikle sayılar teorisinin modüler formlar adı verilen bir bölümünde uzmandı.

Örneğin, Ramanujan hayattayken kimse kara deliklerin incelenecek bir şey olduğunu bile bilmiyordu. Ancak karadeliklerin özelliklerini açıklamak için kullanılan ilk formüllerden bazılarını Srinivasa Ramanujan farkında olmadan geliştirmişti. Bu nedenle günümüzde sayılar kuramı konusunda çalışanlar, Ramanujan’ın defterlerine yazdığı formüller hakkında araştırmalarına devam ediyorlar.

Kendisinin zihninin nasıl çalıştığını daha iyi anlamak için aşağıdaki örneğe göz atın. Günümüzde Pi sayısını hesaplamak için yüzlerce formül vardır. Bu formül de Ramanujan tarafından 1914 yılında yazılmıştır. Elbette kendisinin bu formülü nasıl elde ettiğini bilmiyoruz.

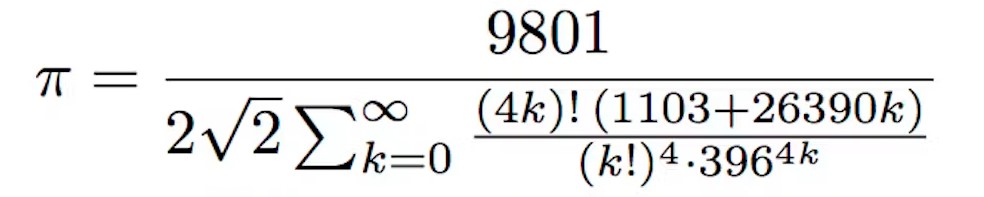
Formül ile ilgili olan ilginç şey ise gerçekten işe yaradığının 1985 yılında ancak bilgisayarların hayatımıza girmesinin devamında ispatlanmasıdır.

Kaynaklar ve ileri okumalar:

• The man who taught infinity: how GH Hardy tamed Srinivasa Ramanujan’s genius. Yayınlanma tarihi: 22 Nisan 2016. Kaynak site: Conversation. Bağlantı: The man who taught infinity: how GH Hardy tamed Srinivasa Ramanujan’s genius
• Ramanujan: Dream of the possible; Kaynak site: Plus Maths. Yayınlanma tarihi: 20 Nisan 2018. Bağlantı: Ramanujan: Dream of the possible
• The Man Who Knew Infinity: a mathematician’s life comes to the movies. yayınlanma tarihi: 17 Kasım 2015. Kaynak site: Conversation. Bağlantı: The Man Who Knew Infinity: a mathematician’s life comes to the movies

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel