Mükemmel Sayı Nedir? Bir Sayı Ne Zaman Mükemmel Olur?

Çoğu matematik öğretmeni, öğrencilere sürekli olarak matematiğin mükemmel olduğunu söyler. O zaman, şimdi matematik camiası tarafından tanımlanan şekliyle sayılarda mükemmelliği tanıyalım. Konumuz mükemmel sayılar.

Kalkülüsün icadından yüzyıllar önce, matematikçiler tam sayıların özelliklerini ve aralarındaki ilişkileri araştırmaya başladılar. Bu nedenle, günümüzde sayı teorisi olarak bilinen bir matematik dalı yani sayıların incelenmesi, en eski matematik disiplinlerinden biri olarak kabul edilmektedir.

Bu alanda, birçoğu yüzyıllar sonra çözülmüş ve hatta çözülememiş büyüleyici sorulara rastlanır. Bu sorulardan bir tanesi de mükemmel sayıları içerir. Gerçekten de, mükemmel sayılar hem matematikçileri hem de matematikçi olmayanları tarih boyunca büyülemiştir. Bunun nedeni anlaşılır tanımlarının, karmaşıklıkları ve gizemleriyle çelişmesidir. ( Göz atmak isterseniz: 2000 Yıllık Çözümsüz Bir Soru: Tek Mükemmel Sayı Var mıdır?)

Mükemmel Sayı Nedir?

Her pozitif tamsayı çarpanlarına ayrılabilir. Bir sayıyı çarpanlarına ayırmak, onu iki tam sayının çarpımı olarak yazmak anlamına gelir. Her sayının çarpanlarından ikisi kendisi ve 1 sayısı olacaktır. Bir sayının kendisi ve 1 sayısından başka çarpanı ( ya da böleni) yoksa da o sayı bir asal sayı olarak kabul edilecektir.

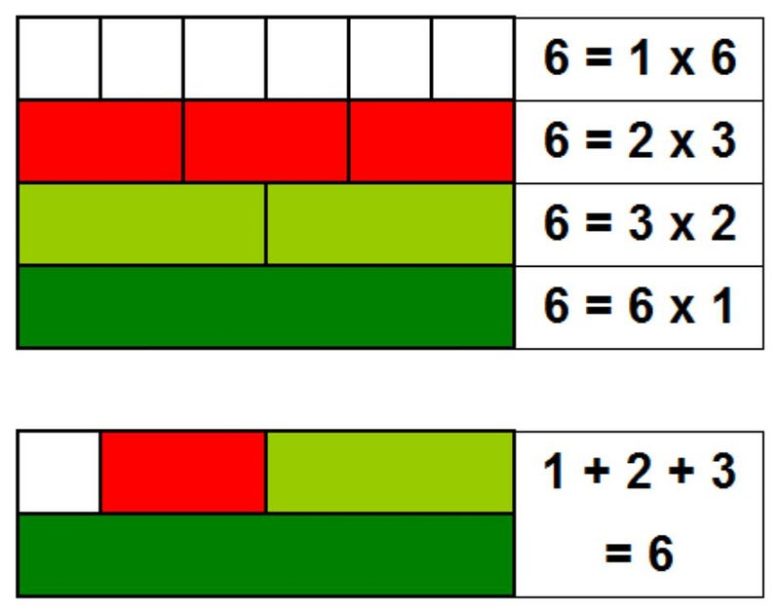
Bir sayıyı çarpanlarına ayırdıktan sonra bu çarpanları toplayabilirsiniz. Bunu yaptığınızda tüm çarpanların toplamı (orijinal sayı hariç) orijinal sayıya eşitse, mükemmel bir sayı buldunuz anlamına gelir. Bunun ne anlama geldiğini 6 sayısı için yukarıda görebilirsiniz.

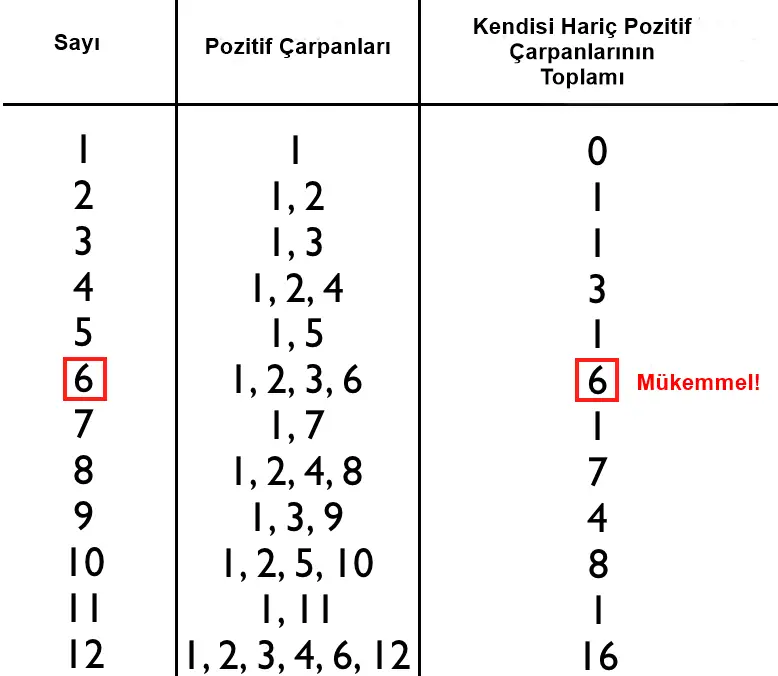
En küçük mükemmel sayı 6’dır. Çünkü bu sayı 6, 2, 3 ve 1’e tam bölünmektedir. Ayrıca 1+2+3=6 toplamına da eşittir. İkinci sırada gelen ise 28 sayısıdır. Bu sayı da 1, 2, 4, 7 ve 14’e bölünür ve 1+2+4+7+14=28’e eşittir.

Mükemmel Sayılar ve Öklid

Mükemmel sayıların hikayesi, yirmi üç yüz yıldan fazla bir süre önce, Öklid ile başladı. Kendisini çoğu zaman bir geometrici olarak düşünsek de aslında Öklid matematiğin birçok dalı üzerinde çalışmalar yaptı. Sayılar teorisi de bunlardan birisi idi.

MÖ 4. yüzyılda Öklid, 2^p − 1 asal ise 2^{p − 1}(2^p − 1) çarpımının mükemmel bir sayı olduğunu kanıtladı. Örneğin, p=2 ise, formül size 2¹× (2² – 1)= 6; p=3 ise 2² × (2³ – 1)=28 sonuçlarını verecektir. Öklid’in “τέλειος ἀριθμός” olarak adlandırdığı mükemmel sayılar gerçekten nadirdir. İlk dört mükemmel sayı 6, 28, 496 ve 8128 biçimindedir. Aslına bakarsanız bin yılı aşkın bir süre boyunca sadece bu dört mükemmel sayı bilinmiştir.

İşin İçine İbnü’l-Heysem’de Dahil Oldu

İbn el-Heysem, matematik, astronomi ve optik konularında eserler kaleme aldı.. Ancak verimli ve başarılı olduğu alan optiktir.

Öklid’in ölümünden bin iki yüz yıl sonra, mükemmel sayılarla ilgili başka bir sonuç için Orta Doğu’ya gitmemiz gerekiyor. İranlı matematikçi İbn el-Heysem, fizik ve optikten sayı teorisi ve geometriye kadar çok çeşitli alanlarda çalıştı. Özellikle, matematiksel yöntemler için Öklid’in Elementlerini detaylı bir şekilde inceledi. Öklid’in önermesinin tersinin de doğru olduğunu öne süren ilk kişi İbnü’l-Heysem’dir: Öklid’in mükemmel sayılar üretme süreci aslında çift olan tüm mükemmel sayıları üretir.

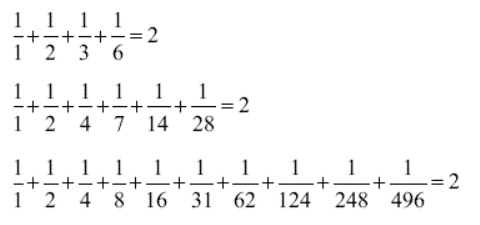
Mükemmel Sayı Nedir? — İlginç bir bilgi: herhangi bir mükemmel sayının bölenlerinin tersini alır toplarsak (bu toplama sayının kendisini de dahil ediyoruz), toplamları her zaman 2’ye eşit olacaktır. Aşağıda bu durum ile ilgili bir kaç örnek görebilirsiniz.

İbnü’l-Heysem bu sonucu tam olarak kanıtlayamasa da, sonraki birçok matematikçi, ek ilerleme sağlamayı umarak Heysem‘in çalışmalarını taklit etmeye çalıştı. Ancak dünya tam bir tanımlamanın ortaya çıkması için yedi yüz yıl daha beklemek zorunda kaldı.

Sonunda her sorunun çözümünde olduğu gibi işin içine yine Euler karıştı. Kendisi Euclid’in mükemmel sayılar üretme algoritmasının aslında her çift mükemmel sayıyı ürettiğini kanıtladı. Buna ek olarak, Euler sekizinci mükemmel sayıyı da tanımladı.

Ünlü matematikçi Leonhard Euler, mükemmel bir sayıya karşılık gelen 2³¹-1 Mersenne asalını keşfetti. Bu asal sayı, 90 yılı aşkın bir süre boyunca bilinen en büyük asal sayı olarak kaldı.

Mükemmel Sayılar Listesi

Peki ya tek ve mükemmel olan sayılar? Tek olan bir mükemmel sayının var olup olmadığını bilmiyoruz; şu ana bulunamamıştır.

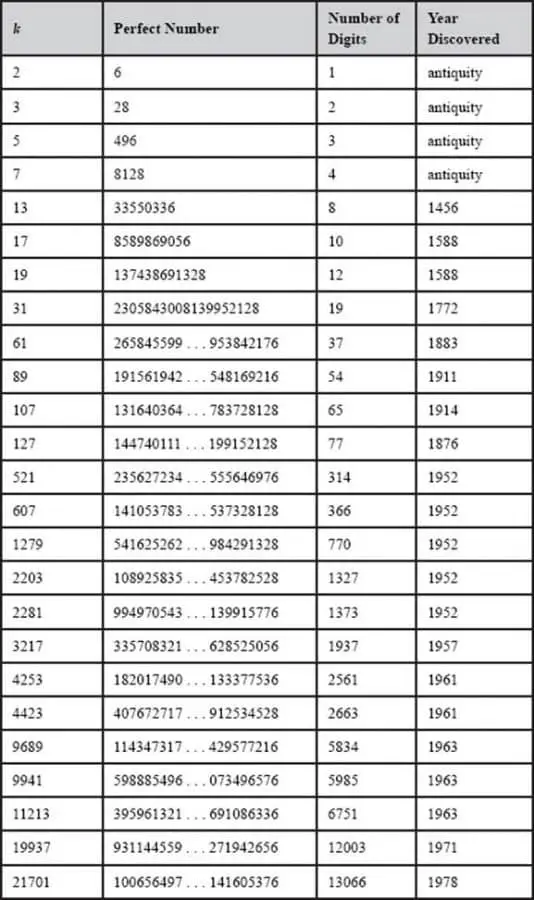
Bugüne kadar 51 mükemmel sayı keşfedildi; en büyüğü 49.724.095 basamaklıdır. Yukarıda mükemmel sayıların bazılarının bir listesini görebilirsiniz. Sonsuz sayıda çift mükemmel sayı var mıdır? Onu da bilmiyoruz. Sonuçta belki de Descartes’ın da dediği gibi, mükemmel sayılar mükemmel insanlar gibi çok azdır, ancak biz yine de aramaktan vazgeçmeyelim.

Bu arada hatırlatalım. Günümüzde asal sayılar üretmek için bir formül bulma çalışmasında mükemmel sayılar önemli rol oynar. Bunun tam olarak ne anlama geldiğini anlamak için de bu yazımıza göz atmalısınız. Bilinen En Büyük Asal Sayı ve Mersenne Asalları

İleri okumalar için: Dylan Johnson; A strange definition of perfect; yayınlanma tarihi: 5 Şubat 2020; Bağlantı: https://plus.maths.org/content/bizarre-definition-perfect

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.