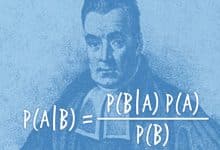Muhtemelen bir çoğumuz normal bir boya, normal bir kiloya sahip olan ortalama insanlarız. Ancak bu tanımın kendisinde bir gariplik var. Sonuçta normal nedir? Ayrıca bu ne anlama gelir? Aslında bir çok şey Adolphe Quetelet ile başladı. Çalışmaları insanların kendileri ve başkaları hakkında neler düşündüğünü derinden etkiledi.
Adolphe Quetelet, 1796’da Belçika’da doğdu. 23 yaşında, Ghent Üniversitesi tarafından verilen ilk matematik doktorasını aldı. Sonrasında zamanının önde gelen bilimsel disiplini olan astronomi ile ilgilenmeye başladı. Ancak bu konuda araştırmalarını sürdürmek için bir gözlemevine ihtiyaç vardı. Belçika’da ise böyle bir gözlemevi yoktu. 1823’te Quetelet bir şekilde Belçika’yı yöneten Hollanda hükümetini Brüksel’de bir gözlemevi inşa etmeye ikna etmeyi başardı. Devamında da Quetelet bu gözlemevinin müdürü oldu.

Yapım devam ederken Quetelet en son gözlem yöntemlerini öğrenmek için Avrupa’daki gözlemevlerini gezmeye başladı. Ancak 1830’da, tam Avrupa turunu tamamlarken, kötü bir haber aldı. Belçika’da devrim olmuştu. İsyancı birlikler yapımı süren gözlemevini ele geçirmişti.
Bu Quetelet için bir belirsizlik süreciydi. Sonuçta işgalin ne kadar süreceğini, yeni hükümetin gözlemevinin tamamlanmasını destekleyip desteklemeyeceği veya hatta Belçika’nın baş astronomu olarak devam etmesine izin verip vermeyeceği hakkında hiçbir fikri yoktu. Bu süreç öncelikle onun hayatında, sonrasında da toplumun bireyleri algılama biçiminde bir dönüm noktası olacaktı.
Normalde Quetelet siyaseti ya da kişilerarası dinamiklerin karmaşıklığını pek önemsemezdi. Odak noktası astronomi idi. Ancak devrim kendi arka bahçesinde patlak verip, süreç onun yaşantısını da etkilemeye başlayınca, insanın sosyal davranışı aniden onun kişisel meselesi haline geldi. Sonrasında aklına bir soru geldi. Toplumu yönetmek için bir bilim geliştirmek mümkün olabilir mi? Quetelet kendine yeni bir hedef belirledi. Astronomi yöntemlerini insanların incelenmesine uygulayacaktı.
Adolphe Quetelet Ve Ortalamaların Hesaplanması
Quetelet’in sosyal davranışı inceleme kararı tarihin uygun bir anında geldi. O sırada uluslar 19. yüzyılın büyük ölçekli bürokrasiler ve ordular geliştirmeye başladıkça, vatandaşları hakkında her ay doğum ve ölüm sayısı, her yıl hapsedilen suçlu sayısı gibi büyük miktarda veriyi tablo haline getirmeye ve yayınlamaya başladılar.
Bu, modern veri toplamanın başlangıcıydı. Ancak hiç kimse bu karmaşık sayı yığınını nasıl faydalı bir şekilde yorumlayacağını bilmiyordu. Ancak Quetelet uzun zamandır rastgele olduğu düşünülen şeylerdeki istatistiksel örüntüleri ortaya koyarak bakış açımızı bütünüyle değiştirdi.
Quetelet’in aklına dönemin astronomlarının yaşadığı bir sorun geldi. O dönemlerde bir gök cisminin hızını ölçmek için nesnenin teleskop camına kazınmış iki paralel çizgi arasından geçiş süresi kaydedilirdi. Ancak bir sorun vardı.
Aynı nesnenin hızını ölçmeye çalışan 10 gökbilimci, genellikle 10 farklı ölçüm bulurdu. Sonunda, gökbilimciler, ortalamalar yöntemi olarak bilinen bir çözümü benimsemişlerdi. Böylece tek tek ölçümler yerine doğru sonucu elde etmek için ortalama ölçümü kullanmaya başladılar. Quetelet bu fikri insanlara uygulamaya karar verdi.
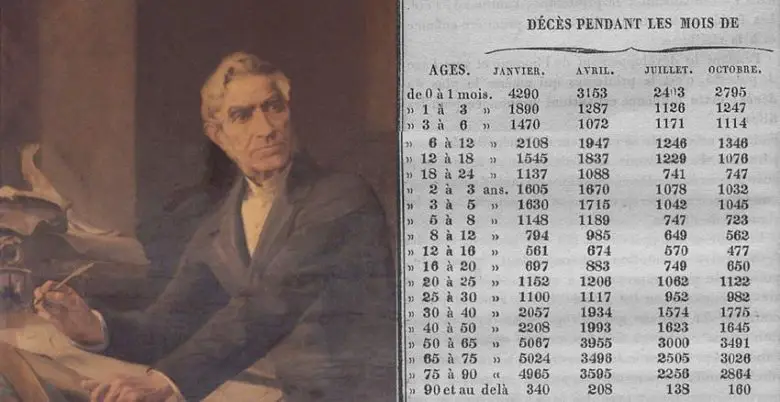
1840’ların başında Quetelet, Edinburgh tıp dergisinde yayınlanan ve 5738 İskoç askerinin göğüs ölçüleriyle ilgili bir çalışmaya rastladı. Quetelet ölçümlerin her birini topladı. Sonra sonucu toplam asker sayısına böldü. Sonuç, bir İskoç askerinin ortalama göğüs çevresini verdi.
Bu sayı, bir bilim insanının herhangi bir insan özelliğinin ortalamasını hesapladığı ilk zamandı. Peki ama bu ortalama tam olarak ne anlama geliyordu? Quetelet bu soruya cevap verebilmek için yine astronomik gözlemleri temel aldı. Sonuçta gökbilimciler, göksel bir nesnenin her bireysel ölçümünün her zaman bir miktar hata içerdiğini bilirdi. Ancak bir grup bireysel ölçümdeki toplam hata miktarını ortalama ölçüm kullanılarak en aza indirmek mümkündü.
Matematikçi Carl Gauss ortalama bir ölçümün, bir ölçümün gerçek değerine oldukça yakın olduğunu göstermişti. Quetelet, aynı düşünceyi insan ortalamalarına uygulamayı düşündü. Örneğin İskoç askerlerinde hesaplanan ortalama göğüs boyutu ideal bir askerin sahip olması gereken boyuttu. Bu boyuta uymayanlar ise bir fiziksel kusur barındırıyordu.
Normal İnsanın Bulunuşu
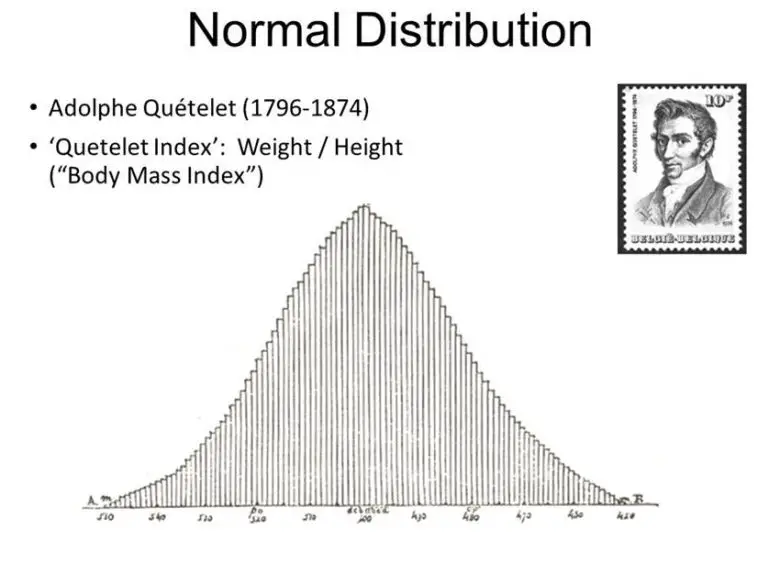
Günümüzde bir kişinin ortalama olduğundan bahsettiğimiz zaman elbette birinin aşağı veya eksik olduğu ima edilmemektedir. Ama Quetelet için ortalama insan, kusursuzluğun kendisiydi. Ardından hızını alamadı, tarihte öne çıkan büyük isimlerin, bulundukları yerin ve zamanın, ortalama insana en yakın olan kişiler olduğunu ilan etti.
Sıradan insanın gizli yüzünü ortaya çıkarmaya hevesli olan Quetelet, veri alabileceği her insan özelliğinin ortalamasını hesaplamaya başladı. Ortalama boy, ortalama ağırlık ve ortalama ten rengini hesapladı. Çiftlerin ortalama yaşını ve insanların ortalama ölüm yaşını hesapladı. Ortalama yıllık doğumları, ortalama yoksulluk içindeki insan sayısını, ortalama yıllık suç olaylarını, ortalama suç türlerini, ortalama eğitim miktarını ve hatta yıllık ortalama intihar oranlarını hesapladı.
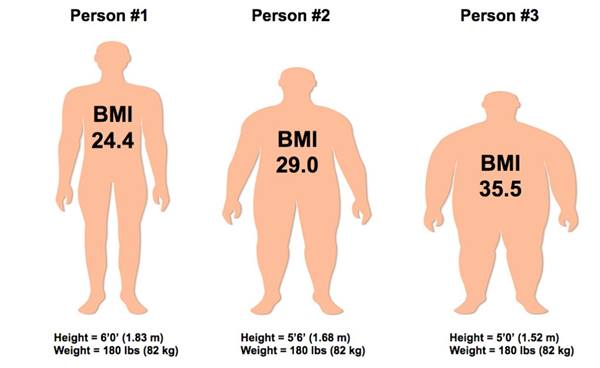
Bugün vücut kitle indeksi veya BMI olarak bilinen Quetelet İndeksini icat etti. Sonrasında ortalama sağlığı belirlemek için erkek ve kadınların ortalama vücut kitle indeksini hesapladı. Quetelet, Ortalama İnsan’a hayran olduğu kadar, ortalamadan sapan talihsiz bireylere karşı da aynı ölçüde antipati duyuyordu. Ona göre ortalama insanın ideal boyutlarından sapan her şey bir şekil bozukluğu ve hastalık anlamı taşıyordu.
Ortalama İnsan Bizler İçin Ne Anlama Geliyor?
İnsan zihninde, “avukatlar”, “evsizler” veya “Meksikalılar” gibi bir grubun tüm üyelerinin bir dizi ortak özelliğe göre belirleme yönünde güçlü bir eğilim vardır. Quetelet’in araştırması bu dürtüye bir temel kazandırmıştır.
Quetelet Ortalama İnsan fikrini ortaya attığından beri, bilim insanları “A Tipi kişilikler”, “nevrotik tipler”, “mikro yöneticiler” ve “lider tipler” gibi görünüşte sonsuz sayıda tipin özelliklerini tanımladılar. üyelerin ortalam özelliklerini yani grubun tipini bilince bir grubun belirli herhangi bir üyesi hakkında, tahminler yapılabileceğini savundular.
Günümüzde ortalamalara alışığız. Günlük medyada sıklıkla ortalama öğrenci borcu miktarını, ortalama izleyici sayısını ve doktorların ortalama maaşını duyarız. Ancak Quetelet yeni bir ortalamayı her açıkladığında o zamanlarda halk şaşkına dönmüştü. Örneğin Quetelet, ortalama intihar oranının yıldan yıla nispeten sabit olduğunu gösterdi.
Bu, bugünlerde pek şaşırtıcı olmasa da, 1830’larda intihar, bir kalıba uyması mümkün olmayan irrasyonel bir karar olarak görülüyordu. Bunun yerine Quetelet, intiharların bir düzenlilik içinde gerçekleştiğini gösterdi. Sadece bu da değil: Var olan düzen, herkesin ortalama bir intihar eğilimine sahip olduğunu da iddia ediyordu.
Quetelet 1874 yılında öldü ancak onun kolektif davranış ile ilgili düşünceleri başka bilim dallarında da yankılarını buldu. Örneğin Fizikçi James Maxwell, klasik gaz mekaniği teorisini formüle etmek için Quetelet’in matematiğinden ilham aldı. Doktor John Snow, Quetelet’in fikirlerini Londra’da kolera ile savaşmak için kullandı. Florence Nightingale, fikirlerini hemşirelikte benimsedi.
Tüm bu varsayımlar nihayetinde nesiller boyu sürdü. Ebeveynler, çocukları ortalama kilometre taşlarına göre gelişmediyse endişelenmeye başladı. Günümüzde sosyal yaşam ve kariyer olarak hepimiz ortalamanın içinde yer almaya çalışıyoruz. Bu dürtüyü Adolphe Quetelet’in araştırmalarına borçluyuz.
Kaynaklar ve ileri okumalar
- Tafreshi D. Adolphe Quetelet and the legacy of the “average man” in psychology. Hist Psychol. 2022 Feb;25(1):34-55. doi: 10.1037/hop0000202. Epub 2021 Sep 13. PMID: 34516191.
- Todd Rose; How the Idea of a ‘Normal’ Person Got Invented; Yayınlanma tarihi: 18 Şubat 2016; Bağlantı: How the Idea of a ‘Normal’ Person Got Invented
Matematiksel